Множество вершин графа называется независимым, если никакие две вершины этого множества не соединены ребром. Задача распознавания: существует ли в заданном графе независимое множество размера не меньше K? Соответствующая ей оптимизационная задача, она же задача о независимом множестве, формулируется следующим образом: в заданном графе требуется найти независимое множество максимального размера. В задаче о максимальном независимом множестве входом служит неориентированный граф, а выходом – максимальное независимое множество в этом графе. Если существует несколько таких множеств, достаточно найти одно.
1. Постановка задачи
Рассмотрим следующую задачу [1, ТГ1]:
Заданы граф 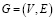 ,
, 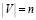 и целое положительное число
и целое положительное число 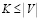 . Существует ли на G независимое множество вершин мощностью не менее K или, иначе говоря, существует ли подмножество
. Существует ли на G независимое множество вершин мощностью не менее K или, иначе говоря, существует ли подмножество 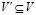 , такое, что
, такое, что 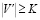 и никакие две вершины из
и никакие две вершины из 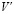 не соединены ребром из E?
не соединены ребром из E?
Пусть 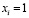 , если вершина
, если вершина 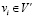 , и
, и 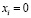 , если
, если 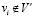 . Сопоставим каждому ребру графа номер
. Сопоставим каждому ребру графа номер 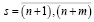 .
.
Тогда, следуя методологии [2], рассматриваемую задачу можно представить в виде целочисленной задачи линейного программирования (1):
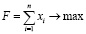 ; (1.1)
; (1.1)
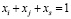 ; (1.2)
; (1.2)
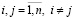 ; (1.3)
; (1.3)
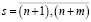 ; (1.4)
; (1.4)
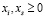 ; (1.5)
; (1.5)
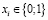 , (1.6)
, (1.6)
где F – целевая функция, равная количеству вершин максимального независимого множества наибольшей мощности; 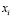 ,
, 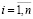 , – переменные, соответствующие вершинам исходного графа G;
, – переменные, соответствующие вершинам исходного графа G; 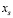 ,
, 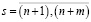 , – переменные, соответствующие рёбрам графа G.
, – переменные, соответствующие рёбрам графа G.
Представим задачу в виде обычной задачи линейного программирования, исключив условие целочисленности (2):
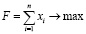 ; (2.1)
; (2.1)
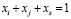 ; (2.2)
; (2.2)
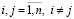 ; (2.3)
; (2.3)
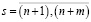 ; (2.4)
; (2.4)
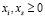 . (2.5)
. (2.5)
Одним из известных способов решения задачи (1) является применение симплекс-метода к задаче (2) и если полученное оптимальное решение целочисленно, то оно является решением и задачи (1). Но, как и во многих других графовых задачах [2-4], представленных в виде ЗЛП, наличие на исходном графе циклов нечётной длины обуславливает, в общем случае, нецелочисленность оптимального решения. В таком случае по последней симплекс-таблице формируют дополнительное ограничение так, чтобы полученное нецелочисленное решение стало недопустимым при сохранении допустимости всех возможных целочисленных решений. Такого рода дополнительные ограничения называются правильными отсечениями, например, отсечение Гомори.
2. Отсечения Гомори для задачи (1)
Пусть на графе G существует цикл C длины k, причем k – нечетное. Тогда в максимальное независимое множество наибольшей мощности 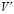 могут войти не более
могут войти не более 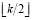 вершин цикла C, поскольку никакие две вершины из
вершин цикла C, поскольку никакие две вершины из 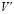 не соединены ребром по определению.
не соединены ребром по определению.
Между тем, применение симплекс-метода к (2) может дать оптимальное решение, компоненты которого, соответствующие циклу C, нецелочисленные, поскольку вклад переменных 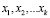 в целевую функцию задачи (2) равен
в целевую функцию задачи (2) равен 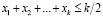 , если переменные нецелочисленные, и
, если переменные нецелочисленные, и 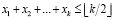 , если переменные целочисленные. При нечётных k справедливо
, если переменные целочисленные. При нечётных k справедливо 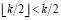 , и при отсутствии каких-либо дополнительных ограничений на эти переменные симплекс-метод может найти именно это оптимальное нецелочисленное решение. Например, если в результате иттераций в базис введены переменные, соответствующие вершинам цикла C, и выведены переменные, соответствующие рёбрам этого же цикла.
, и при отсутствии каких-либо дополнительных ограничений на эти переменные симплекс-метод может найти именно это оптимальное нецелочисленное решение. Например, если в результате иттераций в базис введены переменные, соответствующие вершинам цикла C, и выведены переменные, соответствующие рёбрам этого же цикла.
Поэтому с целью исключения нецелочисленного решения можно выделить все циклы нечётной длины и для каждого явно указать, что
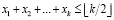 , (3)
, (3)
дополнив (2) соответствующими ограничениями (3).
Покажем, что неравенства типа (3) являются для данной задачи отсечениями Гомори.
Ограничения задачи (2), соответствующие циклу C (рисунок), имеют следующий вид:
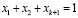 ;
;
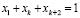 ;
;
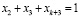 ;
;
…………………
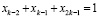 ;
;
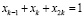 .
.
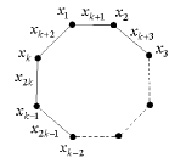
Цикл длины k, xi, 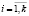 , – переменные, соответствующие вершинам C;
, – переменные, соответствующие вершинам C; 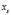 ,
, 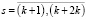 , – переменные, соответствующие рёбрам C
, – переменные, соответствующие рёбрам C
Отсечение Гомори формируется по одной из нецелочисленных строк симплекс-таблицы, пусть это строка, соответствующая переменной 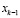 .
.
Пусть базисными переменными оптимальной симплекс-таблицы являются 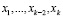 , выразим
, выразим 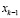 через свободные переменные, подставив в последнее уравнение вместо базисных переменных их выражения через свободные:
через свободные переменные, подставив в последнее уравнение вместо базисных переменных их выражения через свободные:
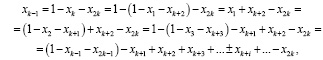
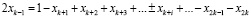 ,
,
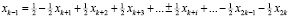 .
.
Сформируем отсечение Гомори:
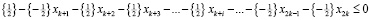 ,
,
где 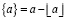 – дробная часть а,
– дробная часть а,
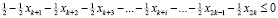 ,
,
с учётом исходной системы ограничений имеем
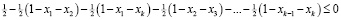 ,
,
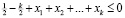 ,
,
в итоге
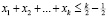 .
.
А так как k – нечётное, то
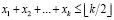 ,
,
что полностью соответствует (3).
4. Метод решения задачи (1)
Будем решать задачу (1) следующим способом. Применим симплекс-метод к задаче (2) и если в ходе иттераций получено нецелочисленное допустимое решение, то останавливаем алгоритм, так как симплекс-метод обнаружил на исходном графе цикл нечётной длины. Тогда, добавив отсечение Гомори к исходной системе ограничений задачи (2), снова применим симплекс-метод, строго соблюдая предшествующий порядок замены переменных, и так далее до получения целочисленного решения. Задачу (2) с дополнительными ограничениями будем далее называть задачей (3).
5. Вычислительная сложность метода
Вычислительная сложность обычного применения симплекс-метода с отсечениями Гомори для задачи (1) определяется вычислительной сложностью собственно симплекс-метода на задачах типа (2) и возможным количеством отсечений.
Известно [7,8], что для общей задачи линейного программирования вычислительная сложность симплекс-метода неполиномиальна по двум причинам.
Во-первых, существует возможность «зацикливания» алгоритма, т.е. многократно повторяемый ввод и вывод из базиса одних и тех же переменных, причём без изменения целевой функции. Во-вторых, коэффициенты при переменных в исходной системе ограничений могут быть таковы, что до получения оптимального решения придётся перебрать все возможные допустимые решения, причём приращения целевой функции на каждой такой иттерации положительны.
Применение стандартных приемов [2-8] позволяет избежать зацикливания алгоритма симплекс-метода, поэтому принципиальное значение имеет вторая причина неполиномиальности симплекс-метода для общей задачи линейного программирования.
Особенностью задачи (2) является то, что максимально возможное значение целевой функции известно заранее и равно n, поскольку мощность любого независимого множества вершин на графе не больше количества вершин этого графа.
С другой стороны, поскольку при получении первого же нецелочисленного допустимого решения работа алгоритма симплекс-метода останавливается, то ненулевые приращения целевой функции задачи (2) в ходе иттераций не менее чем «1». Известно [2, 6], что если алгоритм Блэнда обнаруживает цикл, то при выходе из цикла целевая функция получает положительное приращение. Поэтому нулевые приращения целевой функции при использовании алгоритма Блэнда для рассматриваемой задачи возможны лишь при проведении иттераций с переменными, соответствующими вершинам и рёбрам некоторого дерева. Следовательно, каждое ненулевое приращение будет получено после не более чем O(n) иттераций с нулевым приращением целевой функции.
Таким образом, особенности задачи (2), отличающие её от общей задачи линейного программирования, позволяют оценить вычислительную сложность применения симплекс-метода величиной 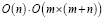 , т.е. не больше
, т.е. не больше 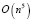 .
.
После каждого добавления к исходной системе ограничений задачи (2) отсечения Гомори алгоритмом строго соблюдается предшествующий порядок замены переменных, что соответствует построению на исходном графе одного и того же дерева. Тогда количество отсечений не больше количества хорд, и для решения задачи (1) предлагаемым способом потребуется не более чем m-кратное применение алгоритма симплекс-метода к последовательности задач (3).
Таким образом, в качестве оценки вычислительной сложности задачи (1) имеем:
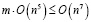 .
.
Следовательно, вычислительная сложность предлагаемого способа решения задачи (1) «в худшем случае» не превышает 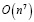 , то есть полиномиальна.
, то есть полиномиальна.
Библиографическая ссылка
Дудов М.Х. МЕТОД ПОСТРОЕНИЯ МАКСИМАЛЬНОГО НЕЗАВИСИМОГО МНОЖЕСТВА НАИБОЛЬШЕЙ МОЩНОСТИ // Международный журнал прикладных и фундаментальных исследований. 2016. № 11-5. С. 868-871;URL: https://applied-research.ru/ru/article/view?id=10547 (дата обращения: 15.01.2026).
DOI: https://doi.org/10.17513/mjpfi.10547

