Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Ткаченко О.П. 1

---

1 Вычислительный центр ДВО РАН

Задача поставлена в контексте проблемы математического моделирования климата планеты. Представлены трехмерные уравнения движения атмосферы, содержащие явно выделенный малый параметр. На основе предложенной замены переменных выполнено преобразование уравнений Навье-Стокса от сферических координат к специальным координатам. В этих новых координатах вычислены символы Кристоффеля и компоненты метрического тензора. Этот подход позволит учесть влияние сложного рельефа на атмосферные явления, которым ранее пренебрегалось. Таким образом, построена новая математическая модель кинематики и динамики атмосферы планеты. Из этой модели, выполняя асимптотические разложения решений уравнений по различным входящим в нее малым параметрам, можно получать частные подмодели для упрощенных задач. Сформулирована новая задача получения уравнений теплового баланса, преобразованных к предложенным переменным.

Статья в формате PDF

918 KB

динамика атмосферы

криволинейная система координат

замена переменных

1. Ландау Л.Д., Лифшиц Е.М. Гидродинамика.– М.: Наука, 1988.– 736 с.

2. Монин А.С. Теоретические основы геофизической гидродинамики.– Л.: Гидрометеоиздат, 1988.– 424 с.

3. Натансон И.П. Краткий курс высшей математики.– СПб.: Лань, 1999.– 736 с.

4. Седов Л.И. Механика сплошной среды.– Т.1.– М.: Наука, 1976.– 536 с.

Исследование движения атмосферы является актуальной задачей геофизической гидродинамики. Уравнения движения принято записывать в квазигоризонтальной форме [2], в которой по высоте вводится гидростатическое приближение

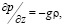(1)

где z – высота над уровнем моря, p – давление, 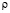– плотность, g – ускорение свободного падения. Но локально в атмосфере на малых высотах могут существовать области, в которых 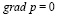для конечных интервалов времени, как правило, в местах со сложным рельефом. На вопрос о влиянии этих областей на динамику относительно большой окрестности атмосферы обращать внимание не было принято. В то же время исследование многомасштабных явлений актуально в связи с задачей точного долговременного прогноза погоды.

Для исследования этого вопроса необходимы трехмерные уравнения движения сжимаемого вязкого газа над поверхностью планеты со сложным рельефом. Здесь выписаны такие уравнения в форме, пригодной для изучения газодинамических процессов. Для выбора различных асимптотик, в том числе квазигоризонтального приближения, уравнения содержат характерные масштабы и малый параметр.

Целью данной работы является построение математической модели кинематики и динамики атмосферы, которая имеет общий характер. Из этой модели, выполняя асимптотические разложения решений уравнений по различным входящим в нее малым параметрам, можно получать частные подмодели для упрощенных задач.

Автор выражает благодарность своему Учителю, академику РАН Вениамину Петровичу Мясникову, за формулировку этой задачи (и многих других задач), и плодотворные обсуждения научных проблем.

1. Соотношения между физическими параметрами атмосферы

За малый параметр естественно принять величину 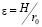, где H – высота однородной атмосферы, 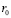– средний радиус планеты. Выражение для H есть в 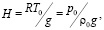[2]:

(2)

где R≈ 287 Дж/кг К – газовая постоянная воздуха, 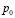, 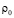– соответствующие температуре T0 давление и плотность воздуха. При 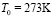высота 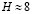км.

Для замены переменных 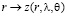необходимо выбрать характерный масштаб 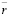, при этом величина 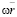будет характерной скоростью для сохранения нелинейных слагаемых в горизонтальном приближении. Здесь 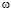– угловая скорость вращения планеты. В качестве уравнения состояния выберем

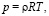(3)

считая воздух идеальным газом. Учитывая выражение для скорости звука

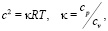
можно выбрать масштаб скорости 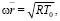откуда получим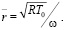

2. Замена переменных

Пусть выбрана сферическая система координат 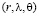с началом в центре планеты и долготой 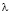. Сделаем замену переменной, предложенную академиком В.П. Мясниковым на семинаре в ИАПУ ДВО РАН в 2002 году:

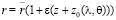, (4)

где z – новая безразмерная переменная, 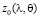– известная функция рельефа поверхности планеты.

С процессом замены переменных связана одна тонкость. Уравнения движения жидкости записаны в инвариантной относительно преобразования координат форме [4]. При покомпонентной записи векторных дифференциальных операторов в различных координатах появляются дополнительные слагаемые без операций дифференцирования, вид и количество которых зависит от выбранной системы координат. Поэтому если от уравнений, выписанных, например, в декартовых координатах, по правилам замены переменных, принятым в скалярном математическом анализе (см. [3]), перейти к другим криволинейным координатам, то вид уравнений может получиться неверным.

Необходимо исходить из инвариантных уравнений движения при переходе к конкретной системе координат. Будем считать, что движение атмосферы можно описать уравнениями Навье-Стокса для сжимаемой жидкости [4]:

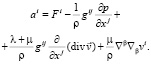(5)

Здесь 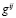– компоненты метрического тензора в выбранной системе координат, 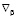– ковариантная производная, 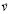– вектор скорости, 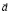– вектор ускорения, 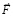– вектор плотности внешних сил, 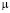– коэффициент вязкости, 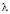– дополнительный коэффициент вязкости. По повторяющимся индексам подразумевается суммирование. Компоненты вектора ускорения выражаются через скорость [4]:

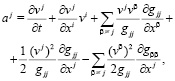(6)

суммирование по j отсутствует. В качестве уравнения состояния выберем (3). В связи с вращением планеты в 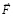, кроме силы тяжести, войдут кориолисова и центробежная силы. Выражения для этих сил, если включать их в правую часть уравнений движения, следующие [1]:

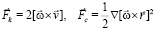. (7)

Здесь обозначено: 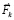– кориолисова сила на единицу массы, 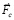– центробежная сила на единицу массы, 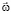– вектор угловой скорости вращения планеты, 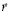– радиус-вектор точки. В сферических координатах 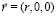, 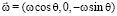. Координаты пронумерованы следующим образом: 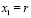, 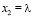(долгота), .

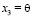3. Уравнения движения и неразрывности в преобразованной системе координат

Для нахождения вида уравнений Навье-Стокса при замене переменной (4) в координатах 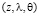были вычислены векторы базиса, компоненты метрического тензора и символы Кристоффеля по формулам из [4]. Мы не приводим здесь эти результаты из-за громоздкости полученных формул. Относительно физических компонент вектора скорости и параметров p, ρ получились, с учетом (7), следующие уравнения движения:

;

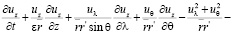
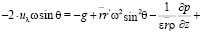
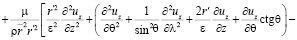
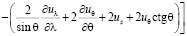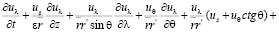
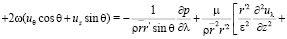
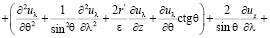
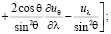
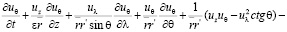
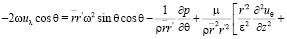
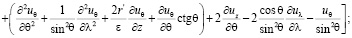
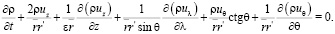(8)

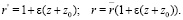
Таким образом, получена система уравнений движения с выделенным постоянным малым параметром ε. Такой подход позволит использовать различные асимптотики решения (8) для разных областей с их последующим сращиванием. Уравнения движения должны быть дополнены уравнениями теплового баланса [2], преобразованными аналогичным образом.

Заключение

Получены трехмерные уравнения движения атмосферы, с явно выделенным малым параметром. Переход к специальным криволинейным координатам позволит учесть влияние сложного рельефа на атмосферные явления, которым ранее пренебрегалось. Кроме того, новая модель позволит исследовать явления различного масштаба в рамках единого подхода. В процессе проведенного анализа возникла новая задача формулировки уравнений теплового баланса, преобразованных к переменным, использованным в основной модели.

Главным результатом статьи является алгоритм применения замены переменной (4) к общим уравнениям гидродинамики, записанным в сферических координатах, и полученная в результате математическая модель.

Библиографическая ссылка