Известно, что наличие твердых или жидких частиц в набегающем потоке может приводить к значительному механическому уносу материалов (эрозии) [3]. В [4] показано, что при движении капель в ударном слое они не только тормозятся, но и разрушаются. В связи с этим представляется интересным рассмотреть влияние экранирующего эффекта ударного слоя на скорость эрозионного разрушения материалов.
В решении задачи для удобства была выбрана система координат связанная с ударной волной. Без потери общности, для упрощения расчётов, рассмотрено движение вблизи оси симметрии. В этом случае приближенно можно считать, что капли движутся в потоке с постоянными параметрами в ударном слое толщиной δ [1].
.
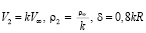Отношение плотностей газа до и после скачка уплотнения в воздухе при скорости набегающего потока V∞ = 2…4 км/c равно k = 0.16…0.11 [1]. Здесь и далее R – радиус носового затупления, r – плотность, индекс «2» относится к параметрам газа за ударной волной, а параметры набегающего потока обозначаются индексом «∞».
В соответствии с экспериментальными данными [4], при расчёте движения капель в ударном слое можно использовать уравнение (1), которое описывает траекторию движения:
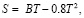(1)
где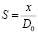 
– безразмерное расстояние; 
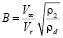– безразмерный коэффициент; 
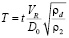– безразмерное время; t– время нахождения капли в ударном слое; δ – отход ударной волны от тела (на оси симметрии); 
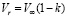– начальная скорость капли относительно потока; ρ2 – плотность за ударной волной; ρd – плотность воды; D0 – начальный диаметр капли.
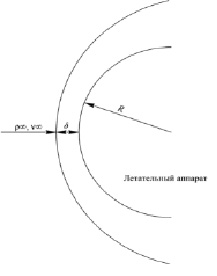
Рис. 1. Схема обтекания
Решая квадратное уравнение (1) можно найти безразмерное время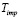 
нахождения капли в ударном слое до соударения с поверхностью:
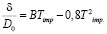
Для нахождения безразмерной скорости, используя уравнение (1), перейдём к дифференциальному уравнению:
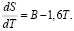
При подстановке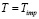 
находится безразмерная скорость капли 
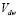около стенки.
Зависимость скорости капли у поверхности тела от её начального размера приведена на рис. 2. Эти результаты получены при следующих условиях: R = 0,1 м;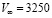 
м/c; 
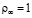г/м3;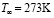 
.
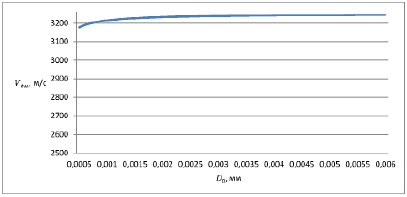
Рис. 2. График зависимости скорости капли у стенки от диаметра (R = 0,1 м;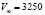 
м/c; 
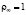г/м3;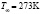 
)
Из графика видно, что капли с размером ~ 100 мкм практически не тормозятся в ударном слое. Этот результат хорошо согласуется с экспериментальными данными.
Выразим абсолютную скорость у стенки через начальную скорость капли относительно потока после прохождения ударногослоя:
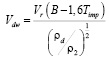. (2)
Найдём зависимость 
для капли диаметром 90 мкм и для разных радиусов притупления ЛА: R=0,1 м, 0,5 м, 1 м (рис. 3).
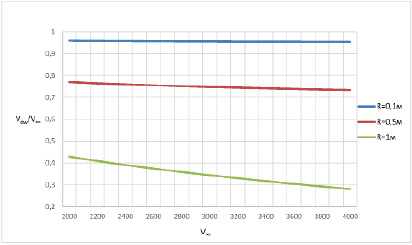
Рис. 3. Зависимость отношения скорости капли у поверхности тела к скорости набегающего потока в зависимосnи от скорости набегающего потока
Как видно из графика, капли почти не тормозятся в ударном слое при радиусе притупления R=0,1 м и весьма сильно теряют скорость при прохождении ударного слоя, возникающего при движении тела с той же скоростью и R=1 м. Такой эффект достигается из-за зависимости от радиуса величины δ – отхода ударной волны от тела и, как следствие, увеличения времени нахождения капли в ударном слое.
Результаты в ударных трубах показали, что существуют два механизма разрушения капель в ударном слое: срыв частичек капель с их поверхности и объёмное «катастрофическое» дробление. Известно [4], что объёмное разрушение капель воды происходит при числах Вебера We>20000 и безразмерном времени пребывания капли в ударном слое больше критического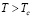 
, причем 
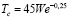. Число Вебера является критерием подобия, определяющего отношение инерции к поверхностному натяжению.
,
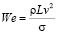где ρ – плотность жидкости; L – характерный размер; v – относительная скорость движения потока; σ – коэффициент поверхностного натяжения.
Подставляя в уравнения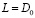 
и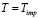 
, находим минимальный размер капли 
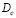, которая достигает поверхности тела.
Процесс уноса массы за счет срыва с поверхности капли можно описать функций безразмерного времени [4]:
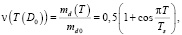
где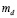 
– масса капли в данный момент времени T; 
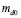– масса капли до вхождения в ударный слой; 
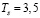– критическое значение безразмерного времени, при котором происходит полное разрушение капли за счёт срыва с поверхности.
Из условия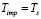 
можно найти минимальный размер капель, при котором масса частицы не теряется полностью вследствие поверхностного срыва:
.
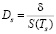Рассмотрев два механизма разрушения капель, мы определили минимальный размер капель, которые долетают до поверхности ЛА:
.
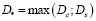До этого момента рассматривалось изменение параметров одной частицы. Для определения скорости эрозионного разрушения необходимо определить параметры водности и среднемассовой скорости частиц у поверхности тела.
Водность капель в данной точке можно найти, используя соотношение 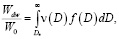[4]:
(4)
где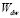 
– водность у стенки в данной точке (массовая концентрация капель); W0 – водность в набегающем потоке; 
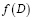– функция распределения капель по размерам.
Спектр крупных капель (больше 20 мкм) для тропических облаков описывается функцией [2]:
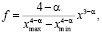(5)
где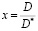 
; D – диаметр частицы; 
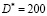мкм; 
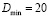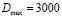мкм; 
мкм;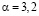 
для тропических облаков с высокой водностью.
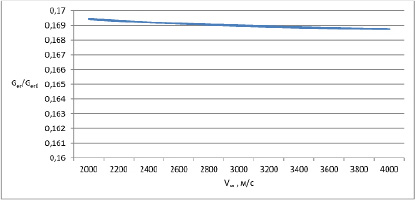
Рис. 4. Зависимость отношения массовых скоростей от скорости набегающего потока (R=0,3 м,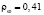 
кг/м3, 
)
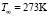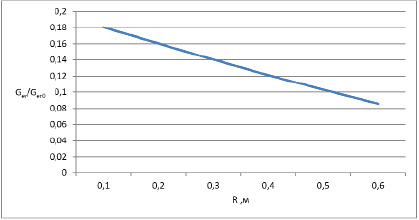
Рис. 5. Зависимость отношения массовых скоростей от радиуса притупления тела (V∞=3000 м/с,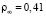 
кг/м3, 
)
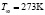Подставляя (3) и (5) в (4), получаем
.
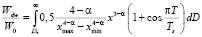Считая интеграл, находим водность у стенки. Проводя аналогичные вычисления, находится среднемассовая скорость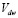 
.
Для определения влияния ударного слоя на скорость эрозионного разрушения, необходимо найти массовую скорость уноса материала поверхности ЛА при наличии ударной волны и без неё.
В [3] показано, что массовую скорость эрозионного разрушения можно найти из соотношения:
,
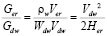где Her – эффективная энтальпия эрозионного разрушения, которая является характеристикой материала.
Для определения влияния ударного слоя на процесс уноса массы тела, найдём отношение скоростей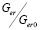 
:
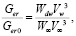
где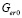 
– массовая скорость эрозионного разрушение при отсутствии экранирующего эффекта ударного слоя (скорость соударения равна 
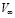, водность 
).
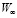Зависимость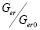 
при постоянном радиусе притупления ЛА и различной скорости набегающего потока (рис. 4) и это же отношение при постоянной скорости набегающего потока и разных радиусах затупления (рис. 5).
Как следует из этих графиков, отношение массовых скоростей эрозионного разрушения слабо зависит от скорости набегающего потока и сильно зависит от радиуса притупления тела.
Заключение
Изменение скорости и размера капель при прохождении ударного слоя (особенно размера) сильно влияют на процесс эрозионного разрушения. Экранирующее воздействие ударного слоя приводит к снижению скорости эрозионного разрушения в ~ 6 раз при R = 0,1 м и в ~ 10 раз при R = 0,5 м.
Библиографическая ссылка
Бегалиев Р.А., Губанов Д.Е., Шматкова М.С. ВЛИЯНИЕ РАЗРУШЕНИЯ И ТОРМОЖЕНИЯ КАПЕЛЬ В УДАРНОМ СЛОЕ НА СКОРОСТЬ ЭРОЗИОННОГО РАЗРУШЕНИЯ МАТЕРИАЛОВ // Международный журнал прикладных и фундаментальных исследований. – 2017. – № 1-2. – С. 218-222;URL: https://applied-research.ru/ru/article/view?id=11171 (дата обращения: 09.09.2024).