В том случае, когда некоторое явление моделируется дифференциальным уравнением, влияние малых параметров на данное явление сводится к изучению зависимости решений уравнения от малых параметров. Сложная ситуация возникает тогда, когда малые параметры содержатся в коэффициентах при старших производных, а при обращении в нуль этих параметров уравнение вырождается. Для уравнений с частными производными обращение в нуль некоторых параметров в главной части уравнения может приводить не к обращению в нуль всей главной части уравнения, а к изменению типа уравнения. Т.к. для уравнений в частных производных для каждого типа уравнений корректны свои задачи, то представляет интерес исследование перехода решения некоторой задачи для уравнения с малым параметром в решение для предельного уравнения. В работе [3] приведен ряд примеров, иллюстрирующих эффекты, возникающие при предельном переходе в уравнении с частными производными.
Рассмотрим задачу Дирихле в полупространстве для уравнения эллиптического типа в следующей постановке:
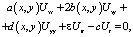 (1)
(1)
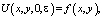 (2)
(2)
ε – малый параметр, ε > 0, 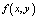 – непрерывная в некоторой области
– непрерывная в некоторой области 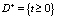 ,
,
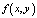
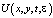 – стремятся к нулю на бесконечности, c const, коэффициенты
– стремятся к нулю на бесконечности, c const, коэффициенты 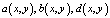 ограничены в полупространстве t > 0 и там же удовлетворяют условию Гёльдера с показателем λ. Это означает, что отношения:
ограничены в полупространстве t > 0 и там же удовлетворяют условию Гёльдера с показателем λ. Это означает, что отношения:
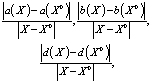
ограничены сверху при любых X и X0, принадлежащих полупространству t > 0.
Предельная задача
Прежде, чем построить решение задачи (1), (2), в уравнении (1) положим ε = 0 и рассмотрим соответствующее ему предельное уравнение:
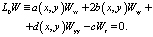 (3)
(3)
Заметим, что уравнение (3) является уравнением параболического типа. Т.е. при ε = 0 порядок уравнения не понизился, но изменился тип уравнения.
Обозначим 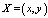 ,
, 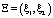 . Норму определим равенством
. Норму определим равенством 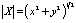 . Будем предполагать, что оператор удовлетворяет следующим условиям:
. Будем предполагать, что оператор удовлетворяет следующим условиям:
1. оператор L0 – равномерно параболический в
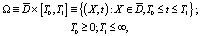
D – неограниченная область 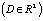 , т.е. существуют положительные постоянные λ0 и λ1 такие, что для любого вещественного вектора
, т.е. существуют положительные постоянные λ0 и λ1 такие, что для любого вещественного вектора 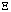
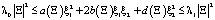
для всех 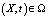 .
.
2. коэффициенты L0 – непрерывные функции в 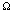 и для всех
и для всех 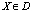 ,
, 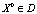 , и некоторого α из интервала
, и некоторого α из интервала 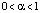 , существует постоянная A, такая, что
, существует постоянная A, такая, что
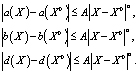
Согласно работе [2], фундаментальное решение уравнения (3) построим методом параметрикса. Для уравнения (3) функция параметрикса имеет вид:
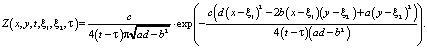 (4)
(4)
Для любых фиксированных 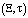 функция
функция 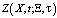 удовлетворяет уравнению с постоянными коэффициентами:
удовлетворяет уравнению с постоянными коэффициентами:
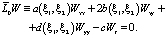
Чтобы построить фундаментальное решение 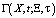 уравнения (3), будем считать
уравнения (3), будем считать 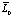 «первым приближением» к L0 и рассматривать Z, как «главную часть» фундаментального решения этого уравнения. Фундаментальное решение
«первым приближением» к L0 и рассматривать Z, как «главную часть» фундаментального решения этого уравнения. Фундаментальное решение 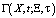 будем искать в виде
будем искать в виде
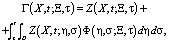 (5)
(5)
где Ф определяется из условия, что 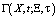 должно удовлетворять уравнению
должно удовлетворять уравнению 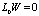 . Этот процесс и называется методом параметрикса. Тогда согласно [2] имеет место соотношение:
. Этот процесс и называется методом параметрикса. Тогда согласно [2] имеет место соотношение:
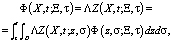 (6)
(6)
где
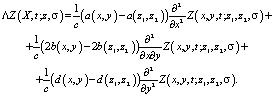 (7)
(7)
Таким образом, для каждых фиксированных 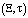 функция
функция 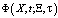 является решением интегрального уравнения Вольтерра с особым ядром
является решением интегрального уравнения Вольтерра с особым ядром 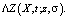 В [2] показано, что особенность ядра интегрируема, а уравнение (6) имеет решение вида:
В [2] показано, что особенность ядра интегрируема, а уравнение (6) имеет решение вида:
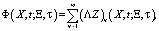 (8)
(8)
где
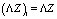
и
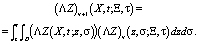 (9)
(9)
Рассмотрим предельную задачу, соответствующую задаче (1), (2):
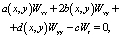 (10)
(10)
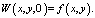 (11)
(11)
Задача (10), (11) есть задача Коши в полупространстве для уравнения параболического типа. Согласно [1], её решение даётся формулой:
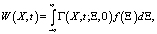 (12)
(12)
где Г – фундаментальное решение, определяемое (5).
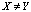
Решение задачи Дирихле (1), (2)
В уравнении (1) введём новую неизвестную функцию 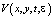 по формуле:
по формуле:
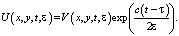 (13)
(13)
В результате получим уравнение:
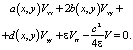 (14)
(14)
Для того чтобы построить фундаментальное решение уравнения (14) в полупространстве t > 0, необходимо знать функцию Леви для этого уравнения. Согласно определению функции Леви, данному в работе [1], надо построить функцию 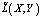 непрерывную вместе со своими производными первого и второго порядка включительно по x, y, t, когда X и Y изменяются в некоторой области С и , и чтобы она при некотором α > 0 удовлетворяла оценкам вида:
непрерывную вместе со своими производными первого и второго порядка включительно по x, y, t, когда X и Y изменяются в некоторой области С и , и чтобы она при некотором α > 0 удовлетворяла оценкам вида:
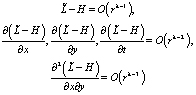 (15)
(15)
равномерно в каждой замкнутой области, содержащейся в C.
Здесь r – расстояние между точками X и Y, 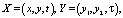
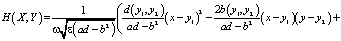
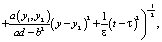
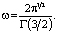
Следуя методике работы [1], построим функцию 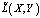 в виде:
в виде:
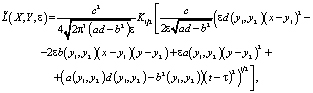
где 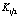 – функция Макдональда, которая есть
– функция Макдональда, которая есть 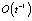 при
при 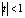 и
и 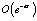 , где a < 1, при t > 1.
, где a < 1, при t > 1.
Функция 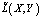 есть функция Леви для уравнения (14) и для достаточно больших r справедливы оценки:
есть функция Леви для уравнения (14) и для достаточно больших r справедливы оценки:
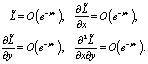
С учетом замены (13), получим функцию Леви для уравнения (1):
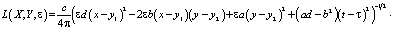
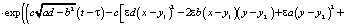
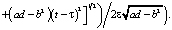
Переходя к пределу, в последнем выражении, получим:
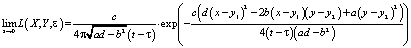 . (16)
. (16)
Как видим, оно совпадает с формулой (4).
Следуя работе [1], фундаментальное решение для (14) будем искать как решение интегрального уравнения:
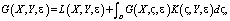 (17)
(17)
которое, в свою очередь, имеет решение вида:
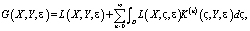 (18)
(18)
где
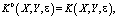
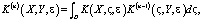
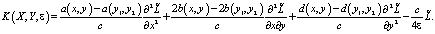
Проведя несложные, но достаточно громоздкие преобразования, с учетом вида функции 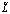 , получим, что:
, получим, что:
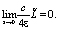
Далее, принимая во внимание выражение (7) получим:
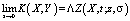 . (19)
. (19)
А с учетом замены (13) и равенств (16), (19), получим:
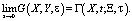 (20)
(20)
Решение задачи (1), (2) будем искать в виде:
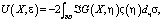 (21)
(21)
где 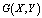 – главное фундаментальное решение уравнения (1). Согласно [1], функция
– главное фундаментальное решение уравнения (1). Согласно [1], функция 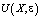 , заданная формулой (21), будет являться регулярным решением задачи (1), (2) в том и только том случае, если для из ∂D
, заданная формулой (21), будет являться регулярным решением задачи (1), (2) в том и только том случае, если для из ∂D
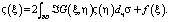 (22)
(22)
С учетом того, что вектор нормали v, выходящий из полупространства D+, имеет направление, противоположное оси , оператор 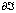 в формуле (22) в данном конкретном случае будет иметь вид:
в формуле (22) в данном конкретном случае будет иметь вид:
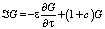 . (23)
. (23)
Принимая во внимание выражения (20), (23) получим, что ядро интегрального уравнения (22) при t = 0 и при > 0 равно 0.
Таким образом, искомое решение задачи (1), (2) примет вид:
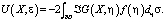 (24)
(24)
Выполнив вычисления под знаком интеграла в (24) с учетом выражений (17), (20), (23), получим, что:
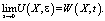
Полученный результат сформулируем в виде теоремы:
Теорема. Если в уравнении (1) c > 0, а остальные коэффициенты ограничены в полупространстве t > 0 и удовлетворяют в этом полупространстве условию Гёльдера с показателем λ, то решение задачи Дирихле для уравнения (1) в полупространстве t > 0 при ε → > 0 стремиться к решению задачи Коши для соответствующего предельного уравнения, которое получается из (1), если в нем положить ε = 0.
Библиографическая ссылка
Захарова И.В. ОДНА ЗАДАЧА ДЛЯ УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ЭЛЛИПТИЧЕСКОГО ТИПА, СОДЕРЖАЩЕГО МАЛЫЙ ПАРАМЕТР В ГЛАВНОЙ ЧАСТИ // Международный журнал прикладных и фундаментальных исследований. – 2017. – № 5-2. – С. 235-239;URL: https://applied-research.ru/ru/article/view?id=11578 (дата обращения: 24.04.2024).

