Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Интыков Т.С. 1 Жакенов Б.К. 1 Исабаев М.С. 1

---

1 Карагандинский государственный технический университет Республики Казахстан

В настоящее время в крупных городах Казахстана имеют место проблемы организации дорожного движения, особенно в их центральных частях. Это связано с повышением уровня автомобилизации и наличием неизменной исторически сложившейся улично-дорожной сети города, а также наличием парковок на проезжей части. Все это приводит к снижению уровня безопасности движения транспортных средств и пропускной способности улично-дорожной сети, которые вызывают предзаторовые и заторовые режимы движения. Радикального улучшения условий движения транспорта в городе на длительную перспективу можно достичь при осуществлении мер градостроительного характера: строительством мостов, тоннелей, пробивкой новых магистралей. Осуществление таких проектов требует значительных финансовых вложений и затрат времени. Анализ показывает, что значительно смягчить ситуацию позволит комплекс мероприятий, связанных с совершенствованием управления транспортными потоками в городе – внедрением компьютеризированных автоматических систем управления дорожным движением (АСУ ДД) на улично-дорожной сети городов.

Статья в формате PDF

2325 KB

транспорт

развитие

безопасность

автомобилизация

организация дорожного движения

имитационная модель

АСУ ДД

перекресток

1. Кременец Ю.А. Технические средства организации дорожного движения : учебник для вузов / Ю.А. Кременец, М.П. Печерский, М.Б. Афанасьев. – М.: ИКЦ «Академкнига», 2005. – 279 с.

2. Врубель Ю.А. Организация дорожного движения. В 2 частях. Часть 1. – Мн: Белорусский фонд безопасности дорожного движения, 1996. – 328 с.

Процесс движения автотранспорта на перекрестке представляет большую сложную систему (БСС), которая характеризуется следующими факторами:

– элементами системы являются автомобили и пешеходы;

– связи между элементами определяются знаками дорожного движения, правилами движения, светофорами;

– колебания и отклонения основных отношений (трендов) системы определяются субъективностью решений водителей и пешеходов;

– система является большой, так как количество элементов значительно;

– система является сложной, так как в ней присутствует воля (решения) водителей и пешеходов.

Таким образом, указанный процесс является БСС, определяемой как совокупность элементов (часть из которых люди) и связей.

Возможно описание системы различными способами, в зависимости от закономерности отношений между элементами:

– детерминированными моделями;

– статистическими моделями.

В каждой БСС присутствуют отношения детерминированные, вероятностные и неопределённые. Не существует методов описания неопределённых систем.

В рассматриваемой БСС часть трендов – детерминирована правилами ПДД, а часть вероятностна: например время накопления.

Основываясь на особенностях рассматриваемой БСС, ограничимся рассмотрением четырехстороннего регулируемого перекрестка (рисунок), сохраняя при этом возможность распространения результатов на перекрестки другой конфигурации.

Перекресток оснащен четырьмя светофорами. Движение происходит по горизонтальной улице 2–4 и вертикальной 1–3.

N1, N2, N3, N4 – количество машин, проезжающих перекресток за цикл; а, б, с и d- светофоры;

л, п и н – индексы, обозначающие движение автотранспорта налево, прямо и направо. Например:

N2л – количество машин, проехавших перекресток с вертикальной улицы 3 на горизонтальную 4 за цикл светофорного регулирования. Символами Тзл, Тж и Тк обозначены время горения сигнала светофора. Так Тза – означает время горения зеленого сигнала светофора а. Время проезда обозначается знаком t с символом улицы выезда и направлением движения. Все параметры времени проезда приведены в матрице (1).

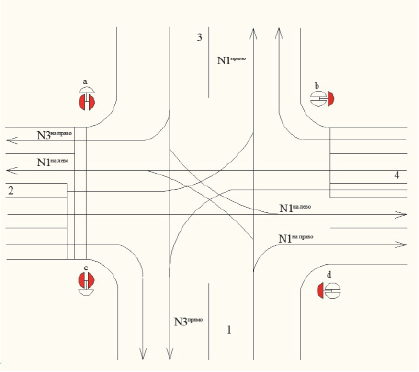
Четырёхсторонний перекресток: 1, 2, 3, 4 – улицы; a, b, c, d – трехсекционные светофоры; N1п, N1н, N1л – соответственно количество имеющих возможность проезда транспорта и приехавшего с улицы 1; N3л, N3н, N3п – соответственно для улицы 3

. (1)

Каждый столбец матрицы описывает время движения с одной улицы, а строка – время движения по одинаковым траекториям.

Например t3л означает время поворота налево автомобиля с улицы 3 на улицу 4. Время проезда связано с направлением проезда:

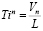, (2)

где L – длина проезда.

Количество проехавших автомобилей будет зависеть от соотношения их габаритов: грузовые к легковым автомобилям. Эту величину γ необходимо определять статистически с учетом коэффициента приведения:

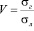, (3)

где σг σл – среднеквадратические отклонения вероятности проезда грузовых и легковых автомобилей.

Считая, что за время цикла Тц проедут Пл автомобилей и Пг грузовых, получим:

Тц = tлПл + tгПг (4)

где tл и tг – соответственно время проезда легковых и грузовых автомобилей. Так как:

Тц = tлПл + tгПг (5)

и Пг + Пл = 100 % (6)

имеем

Пг = VПл. (7)

При дальнейших исследованиях основываясь на полученных зависимостях и коэффициентах приведения, можно учесть длину транспортных средств.

Определим количество приезжающих машин за полный цикл по горизонтальной и вертикальной улицам.

Количество машин, пересекших перекресток после выезда с улицы 1 (см. рисунок), рассчитывается по следующим формулам:

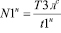; (8)

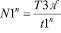; (9)

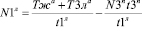. (10)

Смысл управления (10) заключается в том, что количество машин, поворачивающих налево, зависит от суммы времени, остающегося свободным от проезда машин прямо на зеленый сигнал светофора и времени горения желтого сигнала [1].

Уравнения составлены с допущением, что поворот направо и движение прямо происходят одновременно, поэтому необходимо вычесть их количество, определяемое вторым членом правой части управления (10). В этом уравнении, в случае необходимости можно учесть вариант пропуска при повороте налево с улицы 1 машин, движущихся направо с улицы 3. Это учитывается вычитаемым:

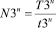. (11)

То есть, в управлении (10) в зависимости от того, какую (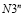 или 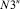) необходимо вычитать величину ( 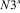или 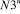). При 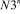> 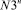справедливо уравнение (10), при 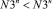, справедливо уравнение (11).

В случае учета движения направо:

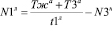. (12)

Или в общем случае:

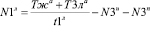. (13)

Зависимость (10) получена из положения, что при отсутствии машин на дороге (3) количество машин, повернувших налево, будет равно:

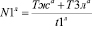. (14)

Величина поворота налево методом просачивания учитывается соответственными статистическими коэффициентами [2].

По аналогии с уравнениями (8)...(10) получены зависимости для количества транспорта по всем улицам:

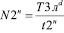; (15)

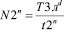; (16)

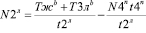; (17)

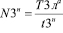; (18)

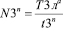; (19)

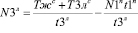; (20)

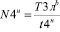; (21)

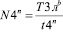; (22)

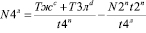. (23)

Сложение всех величин N позволяет получить общее количество транспорта, проезжающего перекресток за один цикл его регулирования.

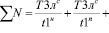
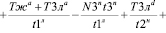
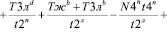
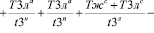
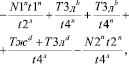(24)

где 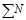– общее количество проезжающего транспорта за один цикл.

Полученная зависимость определяет максимальное количество транспорта, которое может проехать перекресток, и может быть использовано для экологических расчетов.

Для ее использования необходимо вводить граничные условия, отражающие конкретные условия движения. Кроме того, математическая модель должна учитывать вероятностные зависимости наполнения транспорта по разным направлениям.

Как указывалось выше, полученная математическая модель является идеальной. Для анализа реальных моделей необходимо перейти к вероятности насыщения потоков машин, при проектировании и расчете параметров движения на перекрестке и относительном расчете появления при экспериментальных исследованиях. Предположим, относительная вероятность потоков насыщения по разным направлениям определяется матрицей М:

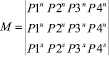, (25)

в которой столбцы списывают количество проехавших машин по направлению движения, а строки вероятности движения по одинаковым перекресткам. При экспериментальных исследованиях вероятность Рi заменяется на относительную частицу появления.

С учетом вероятности насыщения получим количество проезжающих машин прямо по перекрестку:

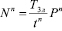, (26)

где индекс п – означает проезд прямо. Тогда время, оставшееся для поворота налево:

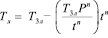(27)

и с учетом желтого сигнала светофора:

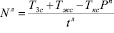. (28)

Эта зависимость характеризует максимальное время, и количество проезжающих машин налево. С учетом вероятности Рл получим

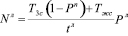. (29)

Например, если Т3с=100 с, Рп =0,7, Рл=0,5, Тжс=10 с, tл=5 c получим:

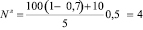автомобиля.

С учетом зависимостей (32), (34) условно на (30) получим вид:

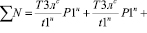
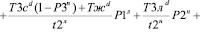
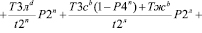
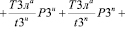
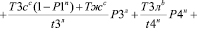
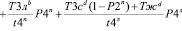.(30)

Или в обобщённом виде:

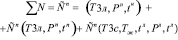.(31)

В соответствии с положениями теории вероятности поворот автомобиля налево оказывается произведением условий вероятности первого события на вероятность второго события.

Условие вероятности в нашем случае описывается зависимостью (34), а произведение вероятностей зависимости (30) логично представить с равными геометрическими параметрами. В этом случае логично допустить, что:

T1н = T2н = T3н = T4н = T1н;

T1п = T2п = T3п = T4п = T1п; (32)

T1л = T2л = T3л = T4л = Tл.

Тогда:

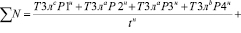
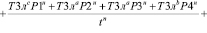
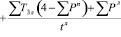(33)

или в коническом виде:

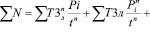
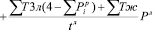. (34)

Полученные зависимости более удобны для расчетов. Если же время горения сигналов двух или более светофоров одинаковы, то полученные зависимости еще более упрощаются.

Научная новизна заключается в разработке имитационной модели движения автотранспорта по перекрестку. Практическая полезность использования разработанной модели заключается в том, что она позволяет, меняя параметры модели, анализировать различные сценарии, в том числе и для движения с поворотом налево.

Библиографическая ссылка