Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Заблоцкий В.Р. 1, 2

---

1 Московский государственный технический университет имени Н.Э. Баумана

2 Московский государственный университет геодезии и картографии

Разработана учебная программа для студентов картографов и геодезистов, изучающих основы программирования на языке С++. Программа вычисляет плоские прямоугольные координаты множества точек, заданных на листе топографической карты. Алгоритм решения задачи заключается в измерении длин перпендикуляров, опущенных от искомой точки на линии километровой сетки карты. Для вычислений координат используется юго-западный угол квадрата, в котором находится искомая точка. С целью получения более точных результатов определения координат в задаче также вычисляются невязки Х и Y координат. Программа демонстрирует применение конструкции повторения – цикла while в варианте бесконечного цикла, остановка которого возможна только путем завершения программы. Несмотря на кажущуюся неопрятность такой конструкции, это позволяет пользователю экономить силы и время и не вводить дополнительные символы с клавиатуры для управления циклом. Также иллюстрируется условная конструкция в сокращенной форме записи и операция явного приведения типа данных. В результате расчета программа выводит на экран значения координат точек – абсциссу и ординату, с точностью до 1 метра. Разработанная программа иллюстрирует решение задачи вычисления плоских прямоугольных координат на основе применения технологии процедурного программирования.

Статья в формате PDF

4104 KB

обучение языку программирования С++

учебная геодезическая задача

вычисление плоских прямоугольных координат точек на карте

1. Готтшлинг П. Современный С++ для программистов, инженеров и ученых. – М.: ООО «И.Д. Вильямс», 2016. – 512 c.

2. Прата С. Язык программирования С++. Лекции и упражнения. 6-е изд. – М.: ООО «И.Д. Вильямс», 2014. – 1248 с.

3. Либерти Дж. Освой самостоятельно С++. 10 минут на урок. 2-е изд. – М.: ООО «И.Д. Вильямс», 2004. – 352 с.

4. Либерти Дж. Освой самостоятельно С++ за 24 часа. 6-е изд. – М.: ООО «И.Д. Вильямс», 2017. – 448 с.

5. Либерти Дж. Освой самостоятельно С++ за 21 день. 3-е изд. – М.: ООО «И.Д. Вильямс», 2001. – 816 с.

6. Zablotskii V.R. Teaching C ++ programming language at Moscow State University of Geodesy and Cartography through the geodesic problems and programs. Proc. 17th International Multidisciplinary Scientific Geoconference SGEM. 2017, Vol. 17, Informatics, Geoinformatics and Remote Sensing, Issue 21, Р. 641–646, 29 June – 5 July, 2017, Albena, Bulgaria.

Несмотря на быстрое развитие науки о компьютерах, обучение программированию еще не прошло этап разделения по отраслям тематических знаний. Практически во всех высших учебных заведениях используется классическая схема преподавания, основанная на программировании задач, как правило, из области математики, одинаково пригодных для будущих инженеров разных специальностей. Однако в настоящее время процесс тематического разделения находится в стадии формирования, о чем косвенно свидетельствует появление, например учебника по программированию Питера Готтшлинга «Современный С++ для программистов, инженеров и ученых» [1]. Очевидно, что нет недостатка в учебниках по программированию на языке С++ универсального типа, и среди них можно отметить классический, многостраничный учебник-справочник Стивена Прата, самоучители Джесси Либерти [2–5]. Однако все эти учебники рассчитаны на широкий круг читателей, и поэтому в них отсутствуют примеры и задачи, ориентированные для профильных инженеров, например картографов и геодезистов.

Нашей целью является разработка набора типовых учебных геодезических программ и задач [4], которые могут использовать как преподаватели, так и студенты, обучающиеся по специальностям картографии и геодезии. Идет работа над сборником задач по программированию по С++ для студентов картографов и геодезистов. В него должны входить задачи геодезического содержания. Приведем несколько примеров таких задач. При изучении темы «Функции, их назначение и использование» уместной является следующая задача. Напишите и запустите программу, которая вычисляет истинный азимут направления с помощью функции TrueAzimuth. Исходные данные – дирекционный угол в градусах и минутах и склонение меридианов в градусах и минутах задается в главной функции, и передаются в функцию TrueAzimuth в качестве параметров, которая вычисляет истинный азимут и выводит результат на экран. Сформулируем еще одну задачу для изучения темы «Условные инструкции и переключатель». Напишите и запустите программу с логической цепочкой if-else-if, которая вычисляет румб направления некоторой линии по ее дирекционному углу. Очевидно, что программирование такого рода задач потребует специальных знаний из области геодезии и картографии. Такие задачи готовят студентов, будущих инженеров геодезистов и картографов, к решению своих специфических задач более эффективно, нежели общие типовые задачи. Автор выносит на обсуждение тезис о том, что разделение курсов программирования по специальностям, на основе создания специализированных лекций, учебников и сборников задач по программированию, есть задача актуальная и ее необходимо решать в настоящее время [6].

В данном сообщении рассматривается учебная программа для студентов картографов и геодезистов, изучающих основы программирования на языке С++, демонстрирующая вычисления плоских прямоугольных координат множества точек, находящихся на топографической карте.

Рассмотрим геодезическую постановку задачи. Пусть задан набор некоторых точек на топографической карте. Требуется вычислить плоские прямоугольные координаты этих точек. Как известно, прямоугольные X и Y координаты вычисляются по формулам

XР = XЮ + ΔXЮ и YР = YЗ + ΔYЗ,

где XЮ и YЮ значения координат юго-западного угла квадрата, в которой расположена заданная точка, ΔXЮ и ΔYЗ приращения координат заданной точки. Для получения более точных результатов определения прямоугольных координат точки в задаче вычисляются невязки Х и Y координат. Поскольку суммы длин перпендикуляров b1 + b2 и a1 + a2, опущенных на противоположные стороны квадрата сетки должны быть равны 1000 м, т.е. длине стороны квадрата километровой сетки, находится разность между вычисленными значениями и истинными. Рассчитанные невязки распределяются между перпендикулярами с обратным знаком в пропорциях определяемых их длинами, например:

,

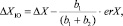
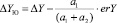где ΔX и ΔX – приращения координат точки, erX, erY ошибки в графическом определении абсциссы и ординаты заданной точки.

Разработанная программа вычисляет плоские прямоугольные координаты заданных на карте точек, используя бесконечный цикл while(1) для многократного повторения вычислений координат точек.

01: #include <iostream>

02: using namespace std;

03:

04: int main (void)

05: {

06: int MapScale;

07: int XcoordinateOfPoint, YcoordinateOfPoint;

08: int XcoordinateSouthWestCornerOfGrid, deltaX;

09: int YcoordinateSouthWestCornerOfGrid, deltaY;

10: double a1, a2, b1, b2, errorX, errorY;

11: double incrementToX, incrementToY, decremtntToX, decremtntToY;

12:

13: while(1){

14: cout <<"Введите знаменатель масштаба карты: ";

15: cin >> MapScale;

16: cout <<"Введите X Y координаты юго-западного угла сетки: ";

17: cin >> XcoordinateSouthWestCornerOfGrid

17: >> YcoordinateSouthWestCornerOfGrid;

18: cout <<"Введите расстояние от точки до западной и восточной"

18: <<" линии рамки километровой сетки (в мм): ";

19: cin >> a1 >> a2;

20: cout <<"Введите расстояние от точки до южной и северной"

20: <<" линии рамки километровой сетки (в мм): ";

21: cin >> b1 >> b2;

22:

23: errorX = (b1 + b2) * MapScale/1000 - 1000;

24: errorY = (a1 + a2) * MapScale/1000 - 1000;

25: cout <<"error X: "<< errorX <<" error Y: "<< errorY << endl;

26:

27: incrementToX = b1 * MapScale/1000 - errorX * b1/(b1 + b2);

28: incrementToY = a1 * MapScale/1000 - errorY * a1/(a1 + a2);

29:

30: deltaX = (int)incrementToX;

31: deltaY = (int)incrementToY;

32:

33: if((incrementToX - deltaX) >= 0.5) deltaX++;

34: if((incrementToY - deltaY) >= 0.5) deltaY++;

35:

36: XcoordinateOfPoint=XcoordinateSouthWestCornerOfGrid *1000 +deltaX;

37: YcoordinateOfPoint=YcoordinateSouthWestCornerOfGrid *1000 +deltaY;

38:

39: cout<<"Coordinates of Point: "<<"X = "<<XcoordinateOfPoint <<"m "

39: <<" Y = " << YcoordinateOfPoint <<"m" << endl;

40:

41: cout <<"Вводите новые данные для расчета: " << endl;

42: }

43: return 0;

44: }

Рассмотрим код программы. В строках 06–08 объявляются переменные целого типа для знаменателя масштаба топографической карты MapScale, Х и Y координат выбранной точки XcoordinateOfPoint, YcoordinateOfPoint, Х и Y координат юго-западного угла километровой сетки XcoordinateOfSWCorner, YcoordinateOfSWCorner, а также приращений координат deltaX, deltaY искомой точки. В строках 09–11 объявляются переменные с плавающей точкой a1, a2 для хранения значений длин перпендикуляров, опущенных из данной точки на западную и восточную сторону квадрата, а также длин перпендикуляров b1, b2, опущенных из данной точки на южную и северную сторону квадрата соответственно. Длины перпендикуляров выражаются в виде целых и десятых долей миллиметров. Переменные errorX, errorY используются для ошибок в графическом определении абсциссы и ординаты заданной точки. Переменные incrementToX, incrementToY, decremtntToX, decremtntToY содержат значения приращений – отрезков в метрах, на которые заданная точка отстоит от юго-западного и северо-восточного угла координатной сетки. Пользователь сначала вводит значение знаменатель масштаба карты, далее значение Х и Y координат юго-западного угла километровой сетки. Отметим, что от данного угла координатной сетки и выполняется расчет координат искомой точки. Затем пользователь вводит значения длин перпендикуляров, опущенных из данной точки на западную и восточную сторону квадрата, а также длин перпендикуляров, опущенных из данной точки на южную и северную сторону квадрата. В строках 23–24 вычисляются невязки координат по X и Y. Полученные результаты выводятся на экран. Затем в строках 27–28 вычисляются приращения абсциссы и ординаты точки по формулам, указанным ранее. Далее в строках 30 и 31 переменные deltaX, deltaY получают приращения координат с точностью до целых метров. При этом используется операция приведения типов, позволяющая взять целое число значений координат (int) incrementToX, (int) incrementToY. Однако при отбрасывании дробной части могут возникать нежелательно большие погрешности, поэтому для устранения погрешностей больших 0,5 м используются условные конструкции вида: if(( incrementToX – deltaX)> = 0,5) deltaX++. Если полученная разность превышает 0,5, то приращение координат увеличивается на 1. Аналогичная инструкция выполняется и для incrementToY. В строках 36 и 37 вычисляются координаты искомой точки XcoordinateOfPoint, YcoordinateOfPoint, для этого координаты юго-западного угла сетки преобразуются в метры умножением на 1000 и добавляется приращение координат. В строке 39 на экран выводится результат вычислений.

Предположим, что пользователь ввел следующие данные: карта масштаба 1:25000, координаты юго-западного угла координатной сетки X = 6065, Y = 4311, длины перпендикуляров (в миллиметрах) соответственно равны a1 = 11,4, a2 = 28, b1 = 23,6, b2 = 16. В результате программа напечатает на экране:

Отметим особенность данной программы, которая заключается в применении бесконечного цикла while(1) для многократного повторения вычислений прямоугольных координат точек. Данный пример демонстрирует, как использовать бесконечный цикл, который в данном случае является полезным инструментом, сокращающим диалог пользователя с программой при ее выполнении. Такой подход имеет определенное преимущество для пользователя, которому не надо каждый раз после выполнения очередного шага цикла вводить дополнительный символ, означающий, что цикл должен быть продолжен или, наоборот, остановлен. Возможны разные варианты создания бесконечных циклов, например с помощью конструкций циклов for, while и do- while. При создании бесконечного цикла while следует поместить в круглые скобки условия, следующего за ключевым словом while ненулевую константу, например число 1, которая будет означать «истину» и цикл никогда не закончится. Такая конструкция цикла подходит для случая, когда программа вычисляет координаты некоторого набора точек по карте и не выполняет дальнейшей обработки полученных координат. По сути дела вычисление координат является основной и заключительной задачей программы. В случае, если такое завершение цикла в программе неприемлемо, можно использовать другой вариант цикла, управляемого изнутри, как например это показано в следующем фрагменте кода:

do

{

. . . . . . . . . . // полезная нагрузка тела цикла

. . . . . . . . . .

cout << "Продолжить программу? Введите (Y/y): ";

cin >> noneStopCharacter;

}while((noneStopCharacter=='Y')||(noneStopCharacter=='y'));

Такой цикл будет многократно выполняться, если пользователь на вопрос «Продолжить программу? Введите (Y/y):», будет вводить букву Y или y. В результате условие ((noneStopCharacter=='Y')||(noneStopCharacter=='y')) получает значение «истина» и цикл продолжается. Очевидное преимущество бесконечного цикла над последним логически более корректным, состоит в отсутствии необходимости ввода букв «Y» или «y» со стороны пользователя.

Еще одно замечание. В решении этой и других задач в геодезической практике часто выполняется контроль вычислений. В рассмотренном случае, например, это контроль координаты Х и Y, который выполняется по формулам: b1 * MapScale/1000 – errorX * b1/(b1 + b2)+ b2 * MapScale/1000 – errorX * b2/(b1 + b2)= 1000 для координаты Х и а1 * MapScale/1000 – errorX * а1/(а1 + а2) + а2 * MapScale/1000 – errorX * а2/(а1 + а2) = 1000 для координаты Y. Нельзя сказать, что теперь при выполнении расчетов на компьютере такие проверки полностью бесполезны. Конечно же, в своих расчетах компьютер не ошибается в отличие от человека. Человек может совершить ошибку в расчетах, компьютер – нет. Однако дополнительная проверка может оказаться полезной при контроле входных данных. Поэтому такого рода проверки можно включать в код программ, полностью следуя алгоритмам обработки исходных данных, применяемым в геодезии. Эти алгоритмы были разработаны именно с учетом «человеческого фактора» и если они переносятся в компьютерные программы, то должны быть веские причины для этого.

Целесообразным в решении данного вопроса является следующий подход. Если в программе переменные инициализируются и отсутствует ввод данных с клавиатуры, то в программе можно не выполнять контроль вычислений. В этом случае возможно написать код программы, конкретно под фиксированные переменные. Если же планируется использовать ввод данных в переменные с клавиатуры, контроль вычислений позволит обнаружить ошибки ввода. В этом случае надо предусмотреть возможные разные значение геодезических величин, чтобы программа могла их корректно обрабатывать. Обычно это усложняет логику программы, приводит к программам с большим объемом кода, однако же делает программу более универсальной.

Выводы

Разработана учебная программа для студентов картографов и геодезистов, изучающих основы программирования на языке С++ в геодезическом вузе. Программа демонстрирует вычисление плоских прямоугольных координат некоторого множества точек, заданных на топографической карте. Подробно описывается код программы и поясняется назначение использованных инструкций. Среди них находятся конструкция повторения или цикл while, условная конструкция if, операция явного приведения типов данных (int), позволяющие округлить полученные значения координат до целых метров. Разработанная программа иллюстрирует решение задачи вычисления плоских прямоугольных координат на основе применения технологии процедурного программирования.

Библиографическая ссылка