Применение сверхкритических флюидов (СКФ) в ракетно-космической технике требует изучения особенностей теплопереноса в объеме СКФ с температурно-плотностными неоднородностями в условиях невесомости. Температурно-плотностная неоднородность в замкнутом объеме СКФ может возникнуть при подводе или отводе тепла со стенок и/или при объемном подводе тепла в результате лазерного нагрева и протекания химических реакций. В космических экспериментах, проведенных на околоземной орбите с помощью аппаратуры АЛИС-1 и АЛИС-2 [1–4], было обнаружено, что температурно-плотностная неоднородность в условиях невесомости является долгоживущей структурой. При достаточном приближении температуры объема СКФ к критической температуре время жизни такой неоднородности в относительно небольшом объеме (с характерным размером 1 см) может достигать нескольких суток.
В перспективных устройствах ракетно-космической техники и химических реакторах для реализации технологических процессов с использованием СКФ возникает необходимость сглаживания (выравнивания) неоднородностей в одних случаях и их усиления (принудительное температурно-плотностное расслоение) в других. Поэтому исследование процессов теплопереноса в замкнутом объеме СКФ при наличии температурно-плотностной неоднородности в условиях невесомости является актуальной задачей.
В настоящей работе исследуются процессы взаимного влияния теплопереноса вблизи критической точки и температурно-плотностной неоднородности при подводе или отводе тепла от границ рабочей зоны и объемного подвода тепла в замкнутом объеме СКФ.
Материалы и методы исследования
Математическая модель
Безразмерная система уравнений состояния, баланса энергии, движения и неразрывности имеет вид
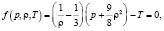 (1)
(1)
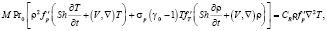 (2)
(2)
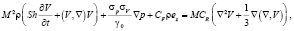 (3)
(3)
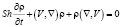 . (4)
. (4)
В уравнениях (1)–(4) использованы традиционные обозначения переменных: p – давление, ρ – плотность, T – температура и V – скорость среды. Далее. Введены следующие безразмерные комплексы (курсивом обозначены размерные величины):
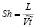 – число Струхала, L – масштаб длины,
– число Струхала, L – масштаб длины, 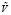 – масштаб скорости и
– масштаб скорости и 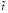 – масштаб времени.
– масштаб времени.
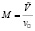 – число Маха,
– число Маха, 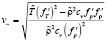 – скорость звука [5] при масштабных термодинамических параметрах
– скорость звука [5] при масштабных термодинамических параметрах 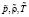 .
.
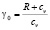 – показатель адиабаты или адиабатическая постоянная.
– показатель адиабаты или адиабатическая постоянная.
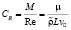 , μ – динамическая вязкость,
, μ – динамическая вязкость, 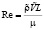 – число Рейнольдса. Параметр CR позволяет сопоставить влияние трения при скоростях диффузионных процессов с влиянием трения, возникающего при движении со звуковыми скоростями в среде с масштабной плотностью в масштабном объеме.
– число Рейнольдса. Параметр CR позволяет сопоставить влияние трения при скоростях диффузионных процессов с влиянием трения, возникающего при движении со звуковыми скоростями в среде с масштабной плотностью в масштабном объеме.
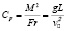 , μ – ускорение свободного падения,
, μ – ускорение свободного падения, 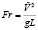 – число Фруда. Параметр CF соотносит потенциальную энергию пробной массы при заданном тяготении на уровне масштабной высоты с кинетической энергией, которую приобретает эта масса, двигаясь со скоростью звука.
– число Фруда. Параметр CF соотносит потенциальную энергию пробной массы при заданном тяготении на уровне масштабной высоты с кинетической энергией, которую приобретает эта масса, двигаясь со скоростью звука.
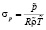 – коэффициент, характеризующий уклонение выбранного масштаба давления от давления совершенного газа при выбранных масштабах плотности и температуры.
– коэффициент, характеризующий уклонение выбранного масштаба давления от давления совершенного газа при выбранных масштабах плотности и температуры.
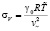 – коэффициент, характеризующий уклонение квадрата скорости звука в совершенном газе при выбранном масштабе температуры от квадрата скорости звука исследуемого газа при масштабных термодинамических параметрах.
– коэффициент, характеризующий уклонение квадрата скорости звука в совершенном газе при выбранном масштабе температуры от квадрата скорости звука исследуемого газа при масштабных термодинамических параметрах.
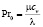 – число Прандтля, λ – коэффициент теплопроводности, cv – удельная теплоемкость при постоянном объеме.
– число Прандтля, λ – коэффициент теплопроводности, cv – удельная теплоемкость при постоянном объеме.
Расчеты проводились для одномерной области длиной L = 1 см в условиях невесомости (g = 0). Рабочее тело – шестифтористая сера (SF6).
Для вычисления безразмерных комплексов, входящих в уравнения (1)–(4) использовались следующие константы (для SF6): cv = 1000 дж/кг×град, λ = 1,2 вт/м×град, μ = 40×10-6 Па×с, R = 56,9 дж/кг×град, γ0 = 1,0569 и масштабы переменных: L = 10-2 м, 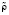 = rкр = 744 кг/м3,
= rкр = 744 кг/м3, 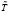 = Ткр = 45,7 °С,
= Ткр = 45,7 °С, 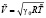 = 134,8 м/c,
= 134,8 м/c, 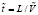 = 7,4×10-5 c.
= 7,4×10-5 c.
Представленная модель использовалась ранее [6] для численного исследования влияния гравитации и перегрузок на теплоперенос в ячейке СКФ.
Степень удаления от критической точки по температуре характеризуется числом ε = T – 1. Удаление от критической точки по плотности определяется параметром m = ρ – 1.
Постановка задачи
Начальные условия задаются следующим образом. В неподвижной среде для заданного значения ε при m = 0 из уравнения (1) определяется давление p0. Для заданного значения m при x∈(0,0.5) плотность ρ1 = 1 + |m|, при x∈(0.5,1) плотность ρ2 = 1–|m|. Температура T1 соответствует плотности ρ1 при давлении p0, температура T2 соответствует плотности ρ2 при давлении p0. Таким образом, в начальный момент времени существует ступенчатое распределение температуры и плотности, а давление постоянно во всей области.
Граничные условия определяются непротеканием в точках x = 0 и x = 1. В точке x = 0 граница считается адиабатической, в точке x = 1 поддерживается температура T2 + DТст., где DТст. температура нагрева или охлаждения стенки и |DТст.|<<T2.
Исследуемый диапазон параметра e составляет 3×10-5 < e < 3×10-3. Параметр m менялся в пределах 0,01÷0,04.
В расчетах определялись зависимости температуры, плотности, скорости и давления от времени в точках x = 0,25; 0,5; 0,75, а также интеграл температуры по длине. По полученным данным определялась характерная величина времени «поршневого эффекта», tПЭ, по методике, описанной ранее [6], и строилась зависимость этой величины от степени приближения к критической точке и разности плотностей в температурно-плотностной неоднородности. Кроме того, определялась степень деформации температурно-плотностной неоднородности в случае подвода и отвода тепла от стенки и в случае объемного подвода тепла.
Результаты исследования и их обсуждение
Зависимость характерного времени «поршневого эффекта» от величины температурно-плотностной неоднородности и близости к критической точке
На рис. 1 представлена зависимость характерного времени «поршневого эффекта» от близости к критической точке (параметр e) при различных значениях величины неоднородности плотности (параметр m).
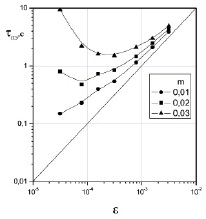
Рис. 1. Зависимость характерного времени «поршневого эффекта» от близости к критической точке (параметр ε) при различных значениях величины неоднородности плотности (параметр m). Значками обозначены расчетные точки
Из рисунка видно, что на достаточном удалении от критической точки (параметр e ≈ 3×10-3) характерное время «поршневого эффекта» почти одинаково для всех значений параметра m, а величина характерного времени близка к его значению для однородной среды с критической плотностью (m = 0). Зависимость характерного времени «поршневого эффекта» от параметра e для однородной среды представлена сплошной линией с наклоном 45 °. По мере приближения к критической точке по температуре (уменьшения параметра e) характерное время поршневого эффекта при наличии неоднородности начинает увеличиваться по сравнению с однородным случаем. Причем чем больше значение m, тем больше отличие. Например, при e ≈ 3×10-5 значения характерного времени поршневого эффекта для m = 0,01 и для m = 0,03 отличаются почти на два порядка.
Интересно сравнить полученные результаты с результатами расчетов для ячейки со сверхкритической температурой и критической плотностью, неоднородность плотности по высоте в которой вызвана наличием силы тяжести и перегрузок [6]. В этом случае температура по высоте постоянна, а плотность и давление распределены по пространству таким образом, чтобы обеспечить механическое равновесие, соответствующее заданному значению ускорения g. При этих условиях тоже наблюдается рост характерного времени «поршневого эффекта» при приближении к критической точке по сравнению с однородным случаем (g = 0). Очевидно, что причиной этого, как отмечалось в этой работе, является усиление неоднородности плотности по пространству. При значениях e, достаточно близких к критическим, и больших значениях перегрузок g = 10g0 распределение плотности близко к ступенчатому распределению. Вдали от критической точки значения tПЭ для всех g очень близки и практически совпадают со значением для однородного (g = 0) случая, поскольку вдали от критической точки эффект сжимаемости мал и плотность практически постоянна по высоте.
В случае температурно-плотностной неоднородности при g = 0 вдали от критической точки, несмотря на большие перепады плотности, значения tПЭ близки к значениям для однородного случая (m = 0). Вблизи критической точки эти значения сильно расходятся для различных значений m. Таким образом, вблизи критической точки в обоих случаях определяющим фактором, влияющим на величину tПЭ , является перепад плотности, а вдали от критической точки перепад плотности не играет существенного значения.
Чтобы убедиться в этом, мы провели сравнение полученных данных для ступеньки плотности и температуры со случаем, когда вся область заполнена менее плотным газом с температурой Т2 и плотностью r2. На рис. 2 представлена зависимость tПЭ от параметра m для различных значений e при наличии (сплошные значки) и отсутствии (открытые значки) температурно-плотностной неоднородности.
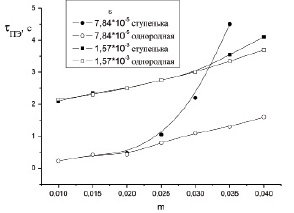
Рис. 2. Зависимость τПЭ от параметра m для различных значений ε. Значками обозначены расчетные точки. Сплошными и открытыми значками показаны значения τПЭ соответственно при наличии и отсутствии температурно-плотностной неоднородности
Из рисунка видно, что вблизи критической точки по мере роста параметра m значения tПЭ сильно растут и при больших m существенно отличаются от однородного случая. Вдали от критической точки наблюдается значительно более слабый рост tПЭ, и значения для неоднородного и однородного случая практически совпадают.
Таким образом, вблизи критической точки наличие перепада (градиента) плотности приводит к увеличению характерного времени «поршневого эффекта» вне зависимости от того, каким способом этот перепад достигнут: за счет перепада температуры при постоянном давлении в невесомости или вследствие установления гидростатического равновесия при постоянной температуре при наличии гравитации (или перегрузки). Увеличение характерного времени «поршневого эффекта» в обоих случаях по все видимости связано с тем, что в неоднородном случае силами давления совершается дополнительная работа по сравнению с однородным случаем. Поскольку «поршневой эффект» по своей природе обусловлен процессом распространения волн давления, плотности и температуры, для выяснения особенностей «поршневого эффекта» в неоднородном СКФ необходимо детальное изучение процесса взаимодействия волн с плотностной неоднородностью.
Деформация температурно-плотностной неоднородности при нагреве и охлаждении границы
На рис. 3 представлен пример временной зависимости отношения разности температур DТ температурно-плотностной неоднородности к начальной разности температур DТнач. при подводе и отводе тепла от границы области повышенной температуры (Т2) для различных значений параметра e и m = 0,03. Верхние ветви кривых (DТ/DТнач. > 1) соответствуют случаю подвода тепла, а нижние ветви кривых (DТ/DТнач. < 1) соответствуют случаю отвода тепла.
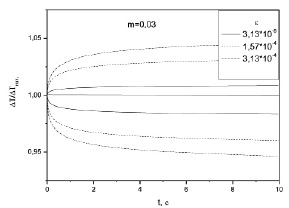
Рис. 3. Временная зависимость отношения разности температур ΔТ = Т2(t) – Т1(t) температурно-плотностной неоднородности к начальной разности температур ΔТнач. = Т2 – Т1 при подводе и отводе тепла от границы при различных значениях параметра ε
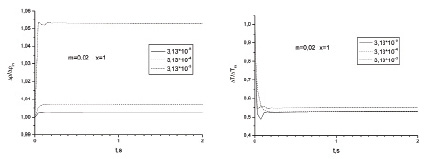
а) б)
Рис. 4. Временные зависимости ступеньки плотности (а) и температуры (б) для m = 0,02 и различных значений ε
Из рисунка видно, что при подводе тепла разность температур в неоднородности растет, а при отводе тепла разность температур уменьшается. При этом данный эффект усиливается по мере удаления от критической точки. Аналогичные зависимости получены и для других значений m.
Деформация температурно-плотностной неоднородности при объемном подводе тепла
Для определения влияния объемного подвода тепла на температурно-плотностную неоднородность были проведены расчеты для случая, когда в начальный момент испытывают разрыв все три термодинамические величины (Т, r, и Р). Как и в предыдущих расчетах, предполагается, что в начальный момент существует ступенчатое распределение температуры (Т1 < Т2) и плотности (r1 > r2) при одинаковом давлении (Р = Р1 = Р2) по длине расчетной области (см. п. 2). Затем, вместо нагрева стенки, как в п. 2, в правой части области устанавливается температура Тнач. (Тнач. > Т2) и соответствующее давление Рнач. (Рнач. > Р), а соотношение плотностей остается неизменным. Такой подъем температуры и давления при неизменной плотности характерен, например, для начального периода лазерного нагрева среды. При прохождении лазерного луча сквозь среду часть энергии лазерного луча поглощается молекулами среды [7]. После включения лазерного излучения температура и давление в облученной области повышается за время значительно меньшее характерного времени развития процессов динамики и теплопереноса, обусловленных возникновением градиентов давления и температуры.
Таким образом, считается, что в начальный момент времени правая половина области оказывается мгновенно нагретой на температуру DТнагр. = Тнач. – Т2, а перепад давления составляет DР = Рнач. – Р. После распада разрыва давление во всей области снова выравнивается и устанавливается температурно-плотностная ступенька с новыми значениями перепадов плотности и температуры.
На рис. 4 представлены примеры временных зависимостей ступеньки плотности (рис. 4, а) и температуры (рис. 4, б) для m = 0,02 и трех значений e (3,13 10-5; 3,13 10-4; 3,13 10-3).
Чтобы охарактеризовать эффективность нагрева среды, можно ввести коэффициент эффективности нагрева aэф. = (DТкон. – DТступ.)/(DТнач. – DТступ.). Коэффициент aэф. характеризует отношение конечного приращения (после распада разрыва) разницы температур в ступеньке к начальному приращению разницы температур (т.е. величине начального нагрева ступеньки). Чем больше коэффициент aэф., тем больше нагревается среда. Важным параметром является отношение величины нагрева к величине ступеньки k = DТнагр./DТступ.. При очень маленьких значениях k нагрев оказывается недостаточным для уверенного определения величины aэф., а при очень больших значениях k в среду будет вноситься слишком большое возмущение и конечная средняя величина температуры будет существенно отличаться от начальной средней величины, по которой определяется параметр e. Для определения оптимального соотношения были проведены расчеты для различных значений k (0,5; 1; 2). Величина k = 1 оказалась оптимальным значением. При k = 1 коэффициент нагрева имеет вид aэф. = DТкон./ DТступ. – 1. В пределе, когда разница температур в ступеньке не увеличивается (DТкон. = DТступ.), значение коэффициента эффективности равно нулю.
На рис. 5 представлена зависимость коэффициента эффективности нагрева aэф. от параметра e для различных значений параметра m. Из рисунка видно, что при всех значениях m эффективность нагрева в целом падает при приближении к критической точке. Причем чем больше параметр m, тем выше эффективность нагрева.
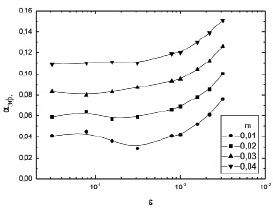
Рис. 5. Эффективность нагрева для различных значений параметра m и ε
Как и в описанном выше случае подвода тепла с границы, для выяснения механизма обнаруженных особенностей нагрева при объемном подводе тепла необходимо детальное исследование взаимодействия генерируемых при этом волн давления, температуры и плотности с плотностной неоднородностью.
Заключение
В работе проведено численное исследование процесса теплопереноса при подводе или отводе тепла на границе и подводе тепла внутри объема сверхкритического флюида при наличии температурно-плотностной неоднородности в условиях невесомости. На основе одномерных уравнений Навье – Стокса, сохранения массы, баланса энергии и уравнения состояния Ван-дер-Ваальса проведены вычисления распределений температуры, плотности, скорости и давления при различном удалении от критической точки по температуре (параметр e) и по плотности (параметр m).
Получено, что в неоднородных условиях при приближении к критической точке по температуре, характерное время «поршневого эффекта», tПЭ, существенно растет по сравнению с однородным случаем при критической плотности (r = 1). При этом чем больше температурно-плотностная неоднородность, тем существеннее рост времени «поршневого эффекта». Сравнение с однородным случаем для разреженного газа (r < 1) показывает, что вблизи критической точки по мере роста параметра m значения tПЭ сильно растут и при больших m существенно отличаются от однородного случая. Вдали от критической точки наблюдается значительно более слабый рост tПЭ, и значения для неоднородного и однородного случая практически совпадают. Это свидетельствует о значительном влиянии перепада плотности на величину tПЭ вблизи критической точки и о слабом влиянии вдали от критической точки. Кроме того, получено, что подвод тепла к области повышенной температуры приводит к усилению, а отвод тепла – к ослаблению начальной температурно-плотностной неоднородности. Объемный подвод тепла в области повышенной температуры и пониженной плотности приводит к усилению температурно-плотностной неоднородности. При этом эффективность нагрева aэф. тем больше, чем сильнее неоднородность (больше m) и в целом уменьшается при приближении к критической точке (параметр e уменьшается).
Необходимо отметить, что для выяснения механизма обнаруженных особенностей нагрева при подводе тепла с границы или объемном подводе тепла в неоднородном сверхкритическом флюиде следует провести детальное исследование взаимодействия генерируемых при этом волн давления, температуры и плотности с плотностной неоднородностью.
Работа выполнена по теме государственного задания «Волновые, конвективные и фрагментационные процессы в сложных жидкостях»; № госрегистрации АААА-А17-117021310375-7.
Библиографическая ссылка
Горбунов А.А., Емельянов В.М., Леднев А.К. ПОВЕРХНОСТНЫЙ И ОБЪЕМНЫЙ НАГРЕВ СВЕРХКРИТИЧЕСКОГО ФЛЮИДА С ТЕМПЕРАТУРНО-ПЛОТНОСТНОЙ НЕОДНОРОДНОСТЬЮ В УСЛОВИЯХ НЕВЕСОМОСТИ // Международный журнал прикладных и фундаментальных исследований. 2019. № 5. С. 135-141;URL: https://applied-research.ru/ru/article/view?id=12752 (дата обращения: 16.01.2026).
DOI: https://doi.org/10.17513/mjpfi.12752

