Явление саморепродуцирования изучено достаточно подробно. Однако влияние на данный эффект фазовых сред различного вида рассмотрено недостаточно. Учет воздействия фазовых сред очень важен для целей практического применения саморепродуцирования, в первую очередь в интерферометрии [1–3]. Решение задачи исследования изменения распределения саморепродукций при прохождении света сквозь прозрачную среду – это последовательный процесс перехода от простых сред, таких как плоскопараллельная пластина, к более сложным, для которых распределение показателей преломления может иметь достаточно произвольный вид.
Целью данной работы является теоретический анализ влияния среды типа прозрачная плоскопараллельная пластина на распределение плоскостей саморепродукции, которое формируется при освещении плоской волной одномерной линейной решетки.
Саморепродуцирование в присутствии прозрачной плоскопараллельной пластины
Эффект саморепродуцирования проще всего рассмотреть на примере регулярного объекта типа одномерная линейная решетка, имеющего пропускающий коэффициент следующего вида [4]:
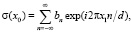(1)
здесь d – период регулярного объекта. Регулярный объект располагают в плоскости, проходящей через начало координат. Плоскость исследуемого прозрачного объекта проходит через точку z2 оптической оси и задается координатами (x2, y2) (рис. 1).
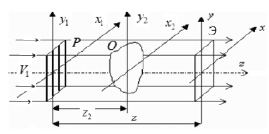
Рис. 1. Схема интерферометра, основанного на явлении саморепродукции: Р – линейная решетка; О – прозрачный объект; Э – экран
Освещаем регулярный объект волной с плоским фронтом и единичной амплитуды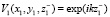 
.
В непосредственной близости за регулярным объектом получаем волну следующего вида:
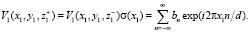(2)
Расположенная вблизи точки z2 исследуемая прозрачная среда воздействует на исходную волну, прошедшую сквозь регулярный объект. До среды волна имеет вид
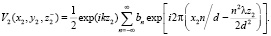(3)
Вид волны, подвергшейся воздействию прозрачной среды V1(x2, y2), описывается следующим соотношением 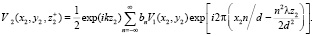[4]:
(4)
Если пропускающая среда не имеет амплитудной составляющей, то она задается следующим выражением
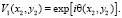(5)
Трансформированная волна, подвергшаяся воздействию прозрачной среды, имеет следующий вид:
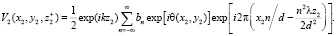(6)
Если следовать схеме, которая представлена на рис. 1, то для распределения интенсивности, измененного объектом, в соответствии с формулой (6), особенности данного распределения задаются искажениями фронта волны, вносимыми рассматриваемой средой. По сути, данное распределение представляет собой многолучевую интерференционную картину, которая формируется в результате интерференции пространственных гармоник, просвечивающих объект под разными углами.
Изменение фазы волны, прошедшей сквозь прозрачную среду, обозначим как θ(x2, y2) [5–7].
Вид волны непосредственно перед исследуемой прозрачной средой представим как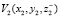 
. Волна, прошедшая прозрачную среду, представляется как произведение фазового распределения исследуемой среды на значение волны перед объектом:
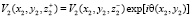. (7)
Модуль амплитуды волны для произвольной координаты z находим по известному значению интенсивности. Фаза волны определяется методом последовательного приближения [4].
Исходя из сказанного, результирующее поле для произвольной точки вдоль оптической оси задается соотношением
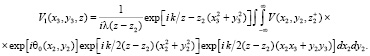(8)
Оставляем неизменным фазовый множитель в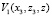 
, а амплитудную часть заменяем на 
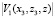. После обратного преобразования Френеля получаем 
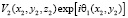. Подставляем рассчитанный фазовый множитель θ1(x2, y2) в (8). Повторяем цикл до тех пор, пока не получаем стационарное решение 
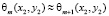, где m – номер итерации. Наибольшее значение m оценивается тем, насколько близко значение θ0(x2, y2) к реальному значению θ(x2, y2). В случае тальбот-интерферометрии интерференционную картину формируют 2M + 1 гармоник, здесь M – максимальный порядок дифракции. Полное число рассматриваемых точек при численных расчетах задаем исходя из общеизвестных положений теоремы отсчетов, которые определяют необходимость описания минимальных неоднородностей среды не менее чем двумя точками дискретизации. Если рассматривать среду, имеющую сложный характер изменения неоднородностей, т.е., в конечном счете, сложный характер распределения показателя преломления фазовой среды, то проблема нахождения фазы волны становится очень сложной, часто просто не имеющей решения, по крайней мере однозначного решения. При рассмотрении более простых пропускающих сред, в нашем случае – это плоскопараллельная пластина, задача нахождения амплитуды световой волны, прошедшей сквозь фазовую среду, становится вполне решаемой даже аналитическими методами [8–9].
Задача оценки влияния пропускающей плоскопараллельной пластины на распределение плоскостей саморепродукции решается с помощью рассмотрения отдельной гармоники, K-й гармоники, ее поведения при прохождении среды толщиной l и показателем преломления n. Для общности рассматриваемой задачи будем считать, что пластина составляет с оптической осью некоторый произвольный угол γ. K-я гармоника световой волны, после прохождения фазовой среды, образует с оптической осью угол θ. Значение этого угла определяется дифракционным условием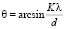 
, где λ – длина световой волны, а d – период регулярного объекта. На рис. 2 схематично представлены направления распространения световой волны, ее К-я гармоника, в отсутствии фазовой среды – линия AM’ и в присутствии пропускающей пластины – линия АСКМ. Угол падения световой волны на пластину равен θ + γ, φ – угол, под которым свет преломляется в фазовой среде.
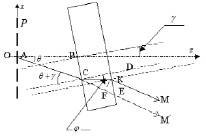
Рис. 2. Воздействие пропускающей плоскопараллельной пластины на К-ю гармонику световой волны
Изменение направления распространения К-й гармоники световой волны при прохождении в фазовую среду определяется соотношением
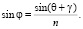(9)
При прохождении пропускающей среды фаза волны, ее К-й гармоники, отличается от фазы этой гармоники в случае отсутствия фазовой среды на величину, определяемую соотношением
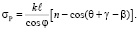(10)
Считая углы θ, γ, φ достаточно малыми, после ряда последовательных преобразований, учитывающих в первую очередь малые значения углов, получаем для изменения фазы световой волны под воздействием плоскопараллельной пропускающей пластины следующее соотношение:
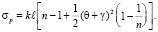(11)
Изменение характера световой волны при удалении ее на произвольное расстояние z от плоскости регулярного объекта, в нашем случае плоской одномерной линейной решетки, можно рассчитать, воспользовавшись соотношением (8) для расчета светового поля:
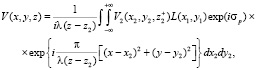(12)
здесь L(x1, y1) – характерные размеры одномерной линейной решетки,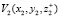 
значение световой волны непосредственно после фазовой среды, которой в нашем случае является пропускающая плоскопараллельная пластина.
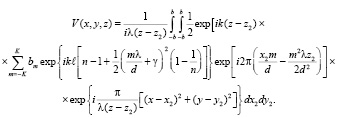(13)
Здесь K – наибольшее значение дифракционного порядка в спектре световой волны после прохождения одномерной линейной решетки.
Преобразование Френеля, которым, по сути, является соотношение (13), легко сводится к преобразованию Фурье.
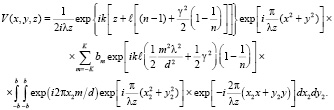(14)
Результирующее соотношение для светового поля, которое представляет собой сформированные линейной одномерной решеткой и фазовой средой типа пропускающая плоскопараллельная пластина распределение в пространстве последовательности саморепродукций, имеет вид
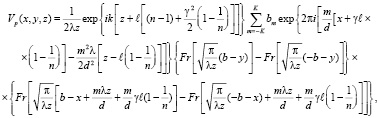(15)
здесь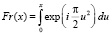 
– интеграл Френеля [10].
Выводы
Проведенный анализ влияния простейшей фазовой среды, типа тонкой плоскопараллельной пластины, на распределение светового поля, формирующего последовательность саморепродукций, установил (формула (15)), что фазовая среда, подобная пропускающей плоскопараллельной пластине, осуществляет смещение саморепродуцированных изображений решетки на расстояние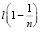 
вдоль оптической оси и на 
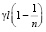в направлениях нормальных оптической оси. То есть общий вид картины саморепродуцированных изображений решетки не изменяется, однако присутствуют смещения вдоль трех взаимно перпендикулярных направлений, которые зависят от трех параметров, таких как толщина и показатель преломления пластины и угол падения световой волны на плоскость пластины. Полученный результат важен с точки зрения разработки интерферометров на основе эффекта саморепродуцирования, в том числе интерферометров голографического типа.
Библиографическая ссылка
Тынышова Т.Д. ИСКАЖЕНИЯ ПОСЛЕДОВАТЕЛЬНОСТИ САМОРЕПРОДУКЦИЙ ПРОЗРАЧНОЙ ПЛАСТИНОЙ // Международный журнал прикладных и фундаментальных исследований. – 2019. – № 5. – С. 142-146;URL: https://applied-research.ru/ru/article/view?id=12753 (дата обращения: 19.04.2024).