Из большого обзора 3D-изображений поверхности высокоэнтропийных покрытий, приведенных в работе [1], можно оценить шероховатость покрытий. Из этой работы видно, что покрытия имеют четко выраженный рельеф, присутствуют как возвышения, так и впадины. Большой объем обзорных работ, посвященных высокоэнтропийным сплавам и покрытиям как отечественных, так и зарубежных изданий, приведен в диссертациях [2–4] и нескольких обзорах (см. ниже). Так, в работах [5; 6] показано, что, несмотря на высокие прочности в литом состоянии, для данных сплавов присуща технологическая пластичность. В процессе деформации в высокоэнтропийных сплавах происходит формирование наноструктуры, которая существенно повышает прочностные характеристики материала. Разрушение в исследованных сплавах имеет характер вязкого излома, и они обладают высокими прочностными характеристиками и пластичностью в исследованном интервале температур. В работах [7; 8] показано, что особенностью высокоэнтропийных сплавов является способность к упорядочению параметра решетки при отжиге, что сопровождается снижением параметра решетки и некоторым повышением модуля упругости и твердости. В обзорах [9–11] показано, что твердость высокоэнтропийного оксидного покрытия достигает значений 27 ГПа при модуле упругости в 270 ГПа, а после отжига при температуре 1100 °С в течение 300 мин. на воздухе снижается до 17 ГПа.
В перечисленных выше работах отмечается, что отсутствует единое мнение о природе, структуре, механизмах и последовательности структурно-фазовых превращений как в литых сплавах, так и в покрытиях.
В настоящей работе, которая является продолжением работ [12; 13], на основе атомно-силовой микроскопии рассматриваются различные механизмы возникновения морфологии осаждаемых покрытий.
Материалы и методы исследования
Для получения магнетронной мишени CrTiNiZrCu методом механического легирования брались микропорошки соответствующих металлов и смешивались в эквиатомных пропорциях [12; 13]. Нанесение покрытий произведено на тщательно отполированных образцах на установке ННВ 6 с магнетронной мишенью. Измерения проводились на атомно-силовом микроскопе JSPM–5400 производства компании JEOL. Для проведения сканирований были применены зонды с резонансной частотой колебаний 40–400 кГц, длиной балки 130 мкм и радиусом скругления острия зонда 10 нм. Для проведения измерений применялся полуконтактный метод сканирования. Размер области сканирования поверхности образцов варьировался от 0,1×0,1 мкм до 0,5 мкм при скорости сканирования 1 нм/с. Наибольшая чувствительность сканирования задавалась при помощи изменения параметров работы микроскопа, например таких, как амплитуда колебаний и коэффициент обратной связи. Затем полученные изображения обрабатывались при помощи программного пакета от компании JEOL для минимизации количества шумов и расчетов интересующих параметров поверхности образцов. Электронно-микроскопическое исследование было проведено на растровом электронном микроскопе MIRA 3 фирмы TESCAN. Исследования проводились при ускоряющем напряжении 20 кВ и рабочем расстоянии около 15 мм. Коэффициенты трения измерялись на разработанной нами установке [14]. Микротвердость измерялась на приборе HVS – 1000.
Результаты исследования и их обсуждение
На рис. 1 показаны 3D-изображения поверхности покрытий CrTiNiZrCu на образцах из стали AISI-201 в трех различных точках, а внизу их фрактальные структуры.
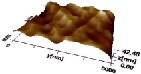





Рис. 1. 3D-изображения поверхности покрытий CrTiNiZrCu в трех различных точках, ниже – их фрактальные структуры
Наблюдается ячеистая структура высокоэнтропийного покрытия CrTiNiZrCu, количественный состав которого показан в таблице. В этой же таблице показан химический состав многокомпонентного алюминиевого сплава, который не относится к высокоэнтропийному покрытию и ячеистая структура которого обнаружена нами ранее [15] и показана на рис. 2.
Количественный химический состав, ат. %
|
Элемент |
Zr |
Ti |
Cr |
Ni |
Cu |
|
CrTiNiZrCu |
23,2 |
21,2 |
19,9 |
17,1 |
6,8 |
|
Элемент |
Al |
Fe |
Mn |
Si |
Cu |
|
AlFeCrMnSiCu |
67,26 |
18,39 |
4,32 |
4,64 |
5,85 |
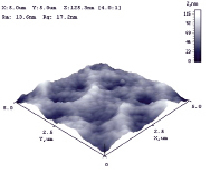
Рис. 2. 3D–изображение покрытия AlFeCrMnSiCu
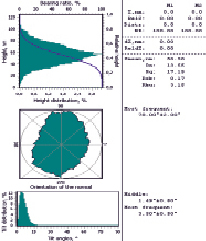
Рис. 3. Гистограмма распределения хиллококов покрытия
Но ячеистая структура наблюдается в покрытиях многих сплавов и соединений [16].

Рис. 4. Трехмерное изображение фрагмента поверхности InSiAs [9]
Мы рассмотрим несколько моделей, приводящих к ячеистой наноструктуре.
Механизм концентрационного переохлаждения [17; 18]. Ячеистая наноструктура возникает, как правило, при кристаллизации в режиме концентрационного переохлаждения [17; 18]. Эта структура состоит обычно из параллельных стержней, которые располагаются в направлении фронта кристаллизации (рис. 5).
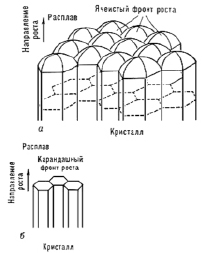
Рис. 5. Ячеистая структура (а) и карандашная (столбчатая) структура (б) [10]
В поперечном сечении структура образует семейство правильных шестиугольных ячеек и представляет собой волновую структуру. После дальнейшего увеличения концентрации примеси на фронте кристаллизации ячеистая структура переходит в дендритную. Модель концентрационного переохлаждения вполне подходит и к нашей модели осаждаемого покрытия, где в качестве примеси может выступать один или все элементы из высокоэнтропийного сплава. Высокоэнтропийный сплав содержит примесей от 5 до 35 ат. % в эквимолярном соотношении. Как правило, он состоит из элементов простой кубической структуры. Однако из этой модели не следует ответ на вопрос о причине самоорганизации покрытия в процессе его осаждения из плазмы.
Конвективная неустойчивость и ячейки Бенара [19; 20]. Для решения вопроса о самоорганизации структурных единиц покрытия рассмотрим модель ячеек Бенара. Ячейки Бенара – это возникновение упорядоченности в виде конвективных ячеек в форме цилиндрических валов или правильных шестигранных фигур в слое вязкой жидкости с вертикальным градиентом температуры (рис. 6) [19; 20].
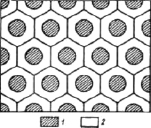
Рис. 6. Схема ячеек Бенара [19]: 1 – восходящее движение, 2 – нисходящее движение
Ячейки Бенара представляют собой один из примеров самоорганизующихся структур. Управляющим параметром служит градиент температур, который приводит к волнообразному возникновению ячеистых структур в однородной жидкости из-за возникновения неоднородности в плотности. Эти диффузионные валы, которые движутся навстречу друг другу, постепенно распадаются на множество волн, образуя ячеистую структуру. Но при дальнейшем увеличении градиента температуры ячеистая структура разрушается и периодические валы постепенно переходят в хаос. Теплопроводность наших покрытий высока и приводит к малому градиенту температур, так что он не может выступать управляющим параметром при образовании ячеистых структур типа ячеек Бенара. При строгом рассмотрении физики ячеек Бенара (см., например, в [19]) в качестве параметра управления обычно выбирают число Релея Re = gL3bdT/νa, где g – ускорение свободного падения, L – характерный размер, b – коэффициент объемного расширения, dT – градиент температуры, ν – кинематическая вязкость, а – коэффициент температуропроводности среды. Кинематическая вязкость обратно пропорциональна величине поверхностного натяжения (поверхностной энергии). Поэтому управляющим параметром в ячеистой структуре должно становиться поверхностное натяжение покрытия, как это указывалось в нашей работе [21].
Ячеистая дислокационная структура. Возникновение ячеистой структуры при образовании плазменных покрытий оказывается не столь простым вопросом. Здесь мы рассмотрим эту модель с привлечением модели ячеистой дислокационной структуры. Она возникает при пластической деформации твердого тела или покрытий на нем и отображает рельеф поверхности на различных уровнях (вплоть до наноструктурного уровня). В работе [22] (см. также ссылки в ней) рассмотрены пять стадий формирования ячеистой дислокационной структуры. Ячеистая дислокационная структура формируется в конце третьей стадии деформационного упрочнения. Эта структура возникает также в процессе самоорганизации (как и ячейки Бенара). Однако механизм самоорганизации связан с размножением и уничтожением дислокаций (рис. 7).

Рис. 7. Ячеистая дислокационная структура в аксонометрической проекции [22]
Ячеистая структура и автоволновые процессы [23]. Оказалось, что локализация пластического течения в металлах и сплавах имеет ярко выраженный волновой характер. При этом на стадиях легкого скольжения, линейного и параболического деформационного упрочнения, а также на стадии предразрушения наблюдаемые картины локализации суть разные типы волновых процессов. Анализ волновых характеристик таких процессов позволил измерить скорость их распространения (~10-4 м/с), длину волны (~10-2 м) и установить, что дисперсионное соотношение для таких волн имеет квадратичный характер. На основании полученных результатов в работе [23] была предложена двухкомпонентная модель пластической деформации, в основе которой лежит взаимодействие фононной и дефектной подсистем в процессе деформирования. Эту модель можно считать достаточно перспективной, поскольку она позволяет правильно оценивать и предсказывать поведение макроскопических картин локализации в процессе пластической деформации металлов и сплавов. На рисунке 8 показана картина ячеистой наноструктуры.
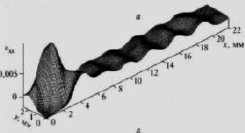
Рис. 8. Распределения локальных удлинений, наблюдаемые на рабочей поверхности деформированного монокристалла кремнистого железа [23]
Ячеистая структура и проблема Стефана [24; 25]. Мы рассмотрели задачу о кристаллизации осаждаемого покрытия в форме цилиндра конечных размеров с подвижной границей раздела фаз [24; 25]. Нестационарное уравнение, описывающее этот процесс в подвижной цилиндрической системе координат, движущейся по закону β(t), имеет вид:
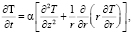
где α – коэффициент температуропроводности.
В результате решение получено в виде:
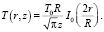
Радиальная и осевая составляющие градиента температуры равны:
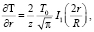
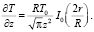
Оба уравнения, содержащие функции Бесселя I0(2r/R) и I1(2r/R), показывают волновой характер затвердевания покрытия (рис. 8).
Развитая нами теория кристаллизации цилиндра конечных размеров относится к задачам с движущейся границей фазового раздела и носит название задачи Стефана [26]. Краевые задачи подобного типа существенно отличаются от классических задач теплопроводности или диффузии. Это отличие связано с движением раздела фаз по произвольному закону, так что разделение переменных классическими методами неосуществимо. Не допускается также метод интегральных преобразований Фурье.
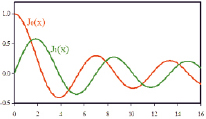
Рис. 9. Графики функций Бесселя (ср. с рис. 8)
Движение фазовой границы приводит к нелинейности системы уравнений, что и вызывает возникновение автоволн.
Заключение
Осаждение покрытий в плазме представляет собой термодинамически неравновесный процесс в открытой системе. Образование ячеистой наноструктуры в покрытии может происходить по нескольким моделям:
– ячеистая субструктура часто образуется при затвердевании в результате возникновения концентрационного переохлаждения;
– ячейки Бенара являются примером самоорганизации. Управляющим параметром самоорганизации служит градиент температуры, приводящей к ячеистой субструктуре;
– ячеистая дислокационная структура является процессом самоорганизации дислокаций в условиях множественного скольжения;
– модель макроскопической локализации пластического течения также дает ячеистую наноструктуру. В этой модели показано, что локализация пластического течения в металлах и сплавах имеет ярко выраженный волновой характер;
– проблема Стефана приводит к нелинейности уравнений, которая возникает из-за движения границы раздела фаз и малой диффузии поверхностных атомов. В этом случае возникает автоволновой процесс.
Работа выполнена по программе МОН РК. Гранты № 0118РК000063 и № Ф.0781.
Библиографическая ссылка
Юров В.М., Гученко С.А., Маханов К.М. АТОМНО-СИЛОВАЯ МИКРОСКОПИЯ ВЫСОКОЭНТРОПИЙНЫХ ПОКРЫТИЙ // Международный журнал прикладных и фундаментальных исследований. 2020. № 4. С. 62-67;URL: https://applied-research.ru/ru/article/view?id=13056 (дата обращения: 14.11.2025).

