В статье рассматривается обратная задача акустики в случае сосредоточенного источника. Исходная задача сводится к системе нелинейных интегральных уравнений Вольтерра второго рода. Для этого с начало рассмотрим обратную задачу акустики [1, 2]
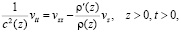 (1)
(1)
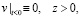 (2)
(2)
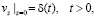 (3)
(3)
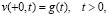 (4)
(4)
где 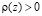 – плотность среды;
– плотность среды; 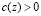 – скорость распространения волн в среде. Прямая (обобщенная начально-краевая) задача (1)–(3) заключается в определении акустического давления
– скорость распространения волн в среде. Прямая (обобщенная начально-краевая) задача (1)–(3) заключается в определении акустического давления 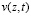 по известным
по известным 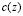 и
и 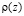 . Прямая задача (1)–(3) корректна, подробнее исследование этой задачи можно найти в работах [3, 4].
. Прямая задача (1)–(3) корректна, подробнее исследование этой задачи можно найти в работах [3, 4].
Материалы и методы исследования
В обратной задаче (1)–(4) по дополнительной информации (4) надо найти либо 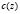 , либо
, либо 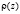 , либо некоторую их комбинацию. Покажем, что одновременно отыскать функции
, либо некоторую их комбинацию. Покажем, что одновременно отыскать функции 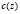 и
и 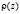 в одномерной постановке невозможно, но их произведение можно найти.
в одномерной постановке невозможно, но их произведение можно найти.
Введем новую переменную
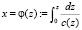 .
.
Поскольку 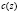 неотрицательна, то для
неотрицательна, то для 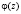 существует обратная функция
существует обратная функция 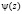 такая, что
такая, что
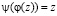 .
.
Обозначим
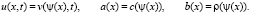
Запишем обратную задачу (1)–(4) в переменных 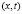 , обозначая
, обозначая 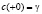
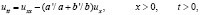
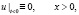
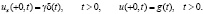
Обозначая 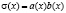 и учитывая, что
и учитывая, что
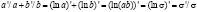 ,
,
получим обратную задачу
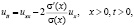 (5)
(5)
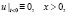 (6)
(6)
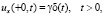 (7)
(7)
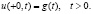 (8)
(8)
в которой по дополнительной информации (8) надо найти решение 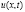 и акустическую жесткость среды
и акустическую жесткость среды 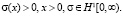
Нетрудно показать, что решение прямой задачи (5)–(7) имеет вид
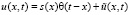 , (9)
, (9)
где 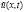 – непрерывная при
– непрерывная при 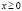 и достаточно гладкая при
и достаточно гладкая при 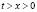 функция,
функция, 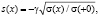 q – тэта-функция Хевисайда.
q – тэта-функция Хевисайда.
Подставляя (9) в систему (5)–(8), получим эквивалентную обратную задачу относительно 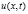 и
и 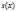
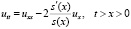 ; (5’)
; (5’)
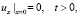 (6’)
(6’)
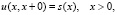 (7’)
(7’)
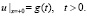 (8’)
(8’)
Обратная задача (5’)–(8’) предпочтительнее первоначальной постановки (1)–(4) по нескольким причинам. Во-первых, прямая задача (5’)-(7’), в отличие от прямой задачи (1)–(3), не имеет сингулярных составляющих. Во-вторых, в обратной задаче (5’)-(8’) не два, а один неизвестный коэффициент s(x). Поэтому после доказательства локальной теоремы существования решения этой задачи станет ясно, что решение исходной обратной задачи (1)–(4) не является единственным, поскольку для одной функции 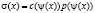 можно подобрать бесконечно много пар функций
можно подобрать бесконечно много пар функций 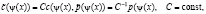 удовлетворяющих исходной обратной задаче. В-третьих, обратную задачу (5’)–(8’) оказывается возможным свести к системе нелинейных интегральных уравнений вольтерровского типа, для которой получена серия результатов, включая теоремы о корректности и о сходимости метода итераций Ландвебера.
удовлетворяющих исходной обратной задаче. В-третьих, обратную задачу (5’)–(8’) оказывается возможным свести к системе нелинейных интегральных уравнений вольтерровского типа, для которой получена серия результатов, включая теоремы о корректности и о сходимости метода итераций Ландвебера.
Сведение обратной задачи акустики к операторному виду. Сформулируем обратную задачу акустики в операторном виде, при этом оставим все обозначения принятые в работе [3].
Обозначим
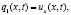
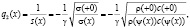
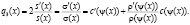
Отметим, что поскольку
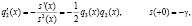
то
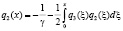 . (10)
. (10)
Используем формулу Даламбера для представления решения задачи Коши (5’), (6’), (8’)
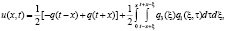 (11)
(11)
и дифференцируем (11) по x
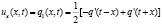
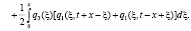 (12)
(12)
Положим в (11) по 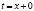
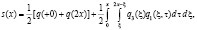
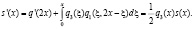
Умножив почленно на (10), получаем
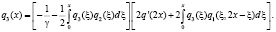 (13)
(13)
Уравнения (12), (10), (13) образуют систему нелинейных интегральных уравнений Вольтерра второго рода. Решение этой системы будем искать в классе 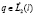 таком, что
таком, что 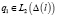 и функции
и функции 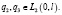 Здесь
Здесь
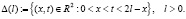
Заметим, что если решение задачи (12), (10), (13) существует и
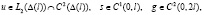
то по формуле 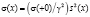 мы можем найти решение обратной задачи (5’)-(7’), при условии, что σ(+0) известно.
мы можем найти решение обратной задачи (5’)-(7’), при условии, что σ(+0) известно.
Результаты исследования и их обсуждение
Исследовать обратную задачу для уравнения акустики (5)–(8) будем в операторной форме
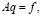 (14)
(14)
где, в соответствии с (12), (10), (13),
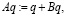 (15)
(15)
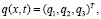 (16)
(16)
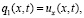
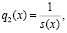
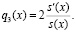
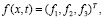 (17)
(17)
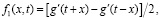
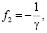
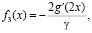
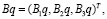 (18)
(18)
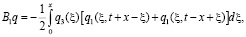
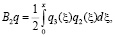
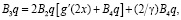
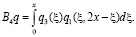
Заметим, что если 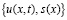 – решение задачи (5’)-(8’), то вектор-функция
– решение задачи (5’)-(8’), то вектор-функция 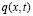 , построенная по формуле (16), является решением задачи
, построенная по формуле (16), является решением задачи 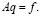
Введем обозначение прямого произведения пространств 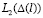 и
и 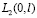 . Будем говорить, что элемент
. Будем говорить, что элемент 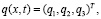 принадлежит пространству
принадлежит пространству 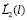 , если
, если
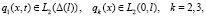
где 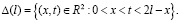
Введем в пространстве 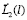 скалярное произведение
скалярное произведение
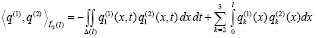 (19)
(19)
и согласованную с ним норму
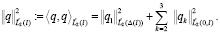 (20)
(20)
Заключение, выводы. В статье рассмотрена обратная задача акустики в случае сосредоточенного источника. Исходная задача сведена к системе нелинейных интегральных уравнений Вольтерра второго рода. Получена операторная форма обратной задачи для исследования свойства оператора производной Фреше и сопряженного к нему оператора.
Библиографическая ссылка
Тюлепбердинова Г.А., Адилжанова С.А. ОБРАТНАЯ ЗАДАЧА АКУСТИКИ И ЕЕ СВЕДЕНИЕ К ОПЕРАТОРНОМУ ВИДУ // Международный журнал прикладных и фундаментальных исследований. – 2015. – № 2-1. – С. 30-32;URL: https://applied-research.ru/ru/article/view?id=6369 (дата обращения: 26.04.2024).

