Постановка задачи
Рассматриваемые физические процессы решаются с помощью методов математического моделирования.
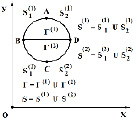
Рис. 1. Некоторое тело, состоящее из двух разных областей Г(1) и Г(2) в прямоугольной декартовой системе координат XOY
Рассмотрим некоторое тело, состоящее из двух разных областей Г(1) (воздушная среда) и Г(2) (твердая среда) (рис. 1) в прямоугольной декартовой системе координат XOY, которому в начальный момент времени t = 0 сообщается механическое воздействие. Предположим, что тело Г(1) изготовлено из деформируемой воздушной среды и является однородным изотропным материалом, подчиняющегося упругому закону Гука при малых упругих деформациях. Если в деформируемом твердом теле предположим, что поперечная скорость распространения равна нулю, то можно получить уравнения состояния для воздушной среды.
Точные уравнения двумерной плоской динамической теории упругости для области Г(1) имеют вид
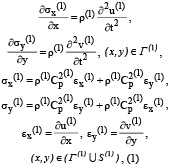
где σx(1) и σy(1) – компоненты тензора упругих напряжений; εx(1) и εy(1) – компоненты тензора упругих деформаций; u(1) и v(1) – составляющие вектора упругих перемещений вдоль осей OX и OY соответственно; ρ(1) – плотность материала; Cp(1) – скорость продольной упругой волны; S(1) (S(1)1 ∪ S(1)2) – граничный контур тела Г(1).
Систему (1) в области, занимаемой телом Г(1), следует интегрировать при начальных и граничных условиях.
Точные уравнения двумерной плоской динамической теории упругости для области Г(2) имеют вид
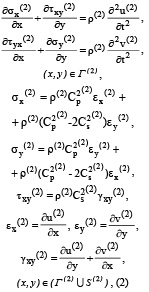
где σx(2), σy(2) и τxy(2) – компоненты тензора упругих напряжений; εx(2), εy(2), и γxy(2) – компоненты тензора упругих деформаций; u(2) и v(2) – составляющие вектора упругих перемещений вдоль осей OX и OY соответственно; ρ(2) – плотность материала; Cp(2) – скорость продольной упругой волны; Cs(2) – скорость поперечной упругой волны; S(2) (S(2)1 ∪ S(2)2) – граничный контур тела Г(2).
Систему (2) в области, занимаемой телом Г(2), следует интегрировать при начальных и граничных условиях. Для решения краевой задачи используется метод конечных элементов в перемещениях.
На основе метода конечных элементов в перемещениях разработаны алгоритм и комплекс программ для решения линейных плоских двумерных задач, которые позволяют решать сложные задачи при нестационарных динамических воздействиях на уникальные сооружения. При разработке комплекса программ использовался алгоритмический язык Фортран-90.
В работах [1–10] приведена информация о моделировании волн напряжений в деформируемых телах с помощью применяемого численного метода.
Решение задачи
о сосредоточенном упругом воздействии в виде дельта функции
Рассмотрим задачу о сосредоточенном упругом импульсном воздействии (рис. 2) на границе воздушной и твердой среды с полостью (рис. 3). Некоторая информация о достоверности применяемого численного метода приведена в следующих работах [1–2, 4–5, 9–10]. В точке В приложено нормальное нестационарное воздействие σy , которое при 0 ≤ n ≤ 10 (n = t / ∆t) изменяется линейно от 0 до P, при 11 ≤ n ≤ 20 изменяется P до 0 (P = σ0, σ0 = - 0,1 МПа). Граничные условия для контура ABCJKI при t > 0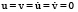 
. Отраженные волны от контура ABCJKI не доходят до исследуемых точек при 0 ≤ n ≤ 200. На границе IHGFEDC приняты условия непрерывности перемещений.
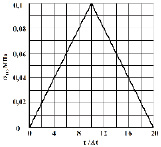
Рис. 2. Воздействие в виде
треугольного импульса
Для области ABCDEFGHI приняты следующие исходные данные:
H = ∆x = ∆y; ∆t = 0,147×10 -4 с; Cp = 340 м/с; ρ = 1,22 кг/м3.
Для области IHGFEDCJK приняты следующие исходные данные:
H = ∆x = ∆y; ∆t = 0,125×10 -4 с; Cp = 400 м/с; Cs = 250 м/с; ρ = 1,469×10 3 кг/м3.
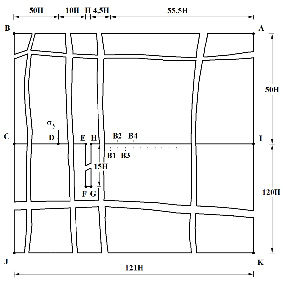
Рис. 3. Постановка задачи о сосредоточенном упругом импульсном воздействии
на границе воздушной и твердой среды с полостью в виде прямоугольника
(соотношение ширины к высоте один к пятнадцати)
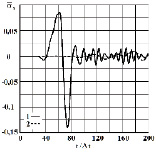
Рис.4. Изменение упругого нормального напряжения ̅σx во времени t / ∆t в точке B1:
1 – в задаче без полости; 2 – в задаче полостью
(соотношение ширины к высоте
один к пятнадцати)
В расчетах принимается минимальный шаг по времени, то есть ∆t = 0,125×10 -4 с. Исследуемая расчетная область имеет 20862 узловых точек. Решается система уравнений из 83448 неизвестных. На рис. 4-7 представлено изменение нестационарного упругого нормального напряжения ̅σх ( ̅σх = σх / |σ0| ) во времени n в точках B1-B4 (рис. 3) находящихся около границы воздушной и твердой среды (расстояние между точками: B1 и B2 равно H; B2 и B3 равно H; B3 и B4 равно H).
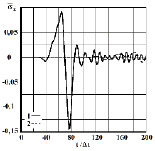
Рис. 5. Изменение упругого нормального напряжения ̅σx во времени t / ∆t в точке B2:
1 – в задаче без полости; 2 – в задаче полостью (соотношение ширины к высоте
один к пятнадцати)
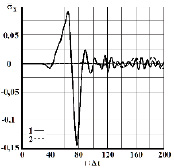
Рис.6. Изменение упругого нормального напряжения ̅σx во времени t / ∆t в точке B3:
1 – в задаче без полости; 2 – в задаче полостью (соотношение ширины к высоте
один к пятнадцати)
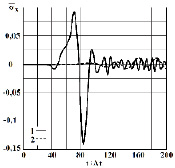
Рис.7. Изменение упругого нормального напряжения ̅σx во времени t / ∆t в точке B4:
1 – в задаче без полости; 2 – в задаче полостью (соотношение ширины к высоте
один к пятнадцати)
Выводы
Полость, с соотношением ширины к высоте один к пятнадцати, уменьшает величину упругого растягивающего нормального напряжения ̅σx в 7,833 раза.
Полость, с соотношением ширины к высоте один к пятнадцати, уменьшает величину упругого сжимающего нормального напряжения ̅σx в 16,0 раз.
Библиографическая ссылка
Мусаев В.К. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ВЕРТИКАЛЬНОГО СОСРЕДОТОЧЕННОГО УПРУГОГО ИМПУЛЬСНОГО ВОЗДЕЙСТВИЯ В ВИДЕ ДЕЛЬТА ФУНКЦИИ НА ГРАНИЦЕ ВОЗДУШНОЙ И ТВЕРДОЙ СРЕДЫ С ПОЛОСТЬЮ В ВИДЕ ПРЯМОУГОЛЬНИКА (СООТНОШЕНИЕ ШИРИНЫ К ВЫСОТЕ ОДИН К ПЯТНАДЦАТИ) // Международный журнал прикладных и фундаментальных исследований. – 2015. – № 2-2. – С. 220-223;URL: https://applied-research.ru/ru/article/view?id=6437 (дата обращения: 21.11.2024).