Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Титова Е.И. 1 Чапрасова А.В. 1

---

1 ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства»

В данной статье рассматривается применение профессионально ориентированных задач на занятиях по математике в строительном вузе. На примере темы «Дифференциальное исчисление» авторами предлагаются три группы прикладных задач, приводятся примеры и выделяются профессиональные качества, формируемые при их решении.

Статья в формате PDF

1213 KB

профессионально ориентированные задачи

преподавание математики в вузе

1. Акимова И.В., Титова Е.И., Чапрасова А.В. Применение ИКТ на занятиях по математике у студентов строительных специальностей для развития профессиональной направленности // Современные проблемы науки и образования. – 2014. – № 5. – С. 145.

2. Бочкарева О.В., Новичкова Т.Ю., Снежкина О.В., Ладин Р.А. Математические задачи как средство формирования профессиональных качеств личности // Современные проблемы науки и образования. – 2014. – № 2. – С. 216.

3. Крымская Ю.А., Титова Е.И., Ячинова С.Н. Построение математических моделей в прикладных задачах // Молодой ученый. – 2013. – № 12 (59). – С. 3–6.

4. Крымская Ю.А., Титова Е.И., Ячинова С.Н. Профессиональная подготовка строителей через решение математических задач // Современные проблемы науки и образования. – 2014. – № 2. – С. 168.

5. Куимова Е.И., Куимова К.А., Титова Е.И. Прикладная направленность курса математики в строительном вузе // Молодой ученый. – 2014. – № 11. – С. 390–391.

Развитие профессиональных качеств у будущих специалистов лежит в основе системы высшего образования. Их формирование не может произойти только на последнем этапе обучения, этого необходимо добиваться постепенно с самого начала и проходить во всех изучаемых дисциплинах. Нам хотелось бы отметить, важность использования прикладных зада на занятиях по математике. Рассмотрим их использование в теме «Дифференциальное исчисление». С учетом выделенных компетенций данной дисциплины для будущих строителей можно выделить следующие группы профессионально ориентированных математических задач:

1 группа. Задачи по технологии и механизации строительного производства, решение которых основано на применении правила нахождения производной. Приведем примеры таких задач.

Задача 1. Найти скорость работы экскаватора (скорость есть первая производная от перемещения по времени) в произвольный момент времени t и в момент времени t = 2 ч. Зависимость проделанной экскаватором работы (т.е. длины выкопанного котлована) от времени выражается формулой .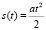

Задача 2. Определить скорость подъема поднимаемой строительным краном бетонной плиты, зная, что скорость 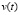является первой производной от перемещения по времени. Зависимость высоты подъема плиты от времени описывается формулой .

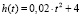2 группа. Задачи по технологии возведения зданий и сооружений. В основном это задачи оптимизационного характера, использующие в своем решении алгоритм нахождения максимального (минимального) значения функции с помощью производной. Рассмотрим примеры подобных задач.

Задача 1. Для придания консоли АВ = а жесткости используются две опоры АD и CD. (рис. 1), где АC = b.

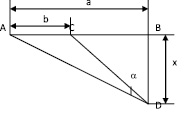
Рис. 1

Наибольшая жесткость конструкции достигается при наибольшей величине угла α, тангенс которого определяется формулой: tg(α) = bx/(x2 + a(a – b)). Определите, на каком расстоянии от точки B следует закрепить опоры, чтобы придать конструкции наибольшую жесткость.

Задача 2. Требуется построить овощной склад с прямоугольным основанием. Периметр основания равен 110 м, высота склада 15 м. Каковы должны быть размеры склада, чтобы он имел наибольшую вместимость?

3 группа. Задачи на исследование эффективности работы механизмов строительных машин. При решении задач данного типа задач студенты составляют математическую модель с привлечением аппарата векторной алгебры, а исследование модели опирается на знание основных понятий физики, умение применять правила дифференцирования функций и умение использовать алгоритмы решений систем линейных алгебраических уравнений. К задачам этой группы можно отнести следующие задачи:

Задача 1: Рассмотрим перемещение звеньев кривошипно-шатунного механизма с заданными размерами (рис. 2).

Допустим, что начальное положение ведущего звена – кривошипа – равно α0 = 62 °. Размеры звеньев кривошипно-шатунного механизма соответственно равны: L = 0,1 и Lc = 0,35. Уравнение движения кривошипа имеет вид: α(t) α₀ + 0,5 t. Требуется определить положение, скорость и ускорение ведомого звена – ползуна кривошипнo-шатунного механизма и их значения для заданного угла поворота.

Задача 2. Рассмотрим перемещение звеньев манипулятора промышленного робота с заданными размерами (рис. 3).

Известны:

– уравнения движения захвата манипулятора

,

.

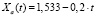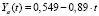– начальные положения звеньев манипулятора – углы расположения звеньев равны:

α₀ = 62 °= 1,082 рад,

β₀ = 33 °= 0,576 рад,

γ₀ = 14 °= 0,244 рад.

– размеры звеньев манипулятора:

а = 1,2,

b = 1,1,

c = 0,55,

s = 0,411.

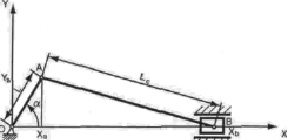
Рис. 2. Схема кривошипно – шатунного механизма

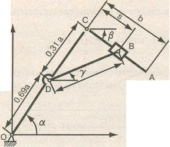
Рис. 3

Требуется определить значения угловых скоростей и ускорения звеньев манипулятора.

Проведя анализ решения этих групп задач, мы выделили профессиональные качества, формируемые в процессе решения представленных типов задач.

Для задач первой группы таковыми являются:

1) профессиональное умение – умение применять математический аппарат при вычислении скорости протекания строительных процессов;

2) взаимосвязь математики с такой строительной дисциплиной как технология и механизация строительного производства, которая выражается в умении применять правила нахождения производной при исследовании строительных процессов;

3) профессиональная мотивация, формирующаяся в ходе применения математического аппарата данного раздела в указанной строительной отрасли.

При решении задач второй группы формируются следующие качества:

1) профессиональное умение – умение на основе использования математических методов находить оптимальные решения при сооружении строительных конструкций;

2) связь метода нахождения максимального (минимального) значения функции с помощью производной со специальной дисциплиной «Технология возведения зданий и сооружений»;

3) профессиональная мотивация, при показе применения вышеуказанного метода в данной строительной отрасли.

Третий тип задач предполагает формирование таких качеств:

1) профессионального умения – умения с помощью математических средств исследовать эффективность работы механизмов строительных машин;

2) взаимосвязи аппарата векторной алгебры, правил нахождения производных, методов решения систем линейных уравнений и строительной дисциплины «Технология и механизация строительного производства»;

3) профессиональной мотивации в ходе использования аппарата линейной и векторной алгебры, а также теории дифференциальных исчислений функций одной переменной в решении строительных задач.

Представленные группы задач позволяют формировать профессиональные качества личности будущего строителя, позволяет ему видеть перспективы своей профессии и целесообразность изучения данного предмета.

Библиографическая ссылка