Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Ложкин Л.Д. 1 Солдатов А.А. 1 Майоров А.Г. 1

---

1 Поволжский государственный университет телекоммуникаций и информатики

В работе рассматриваются антенны на основе подмагниченного гиромагнитного резонатора (ГР). Подмагниченный гиромагнитный резонатор возбуждается через фидерную линию СВЧ-полем и затем, в свою очередь, возбуждает объемный резонатор ОР или рупорную антенну, которые излучают в пространство электромагнитное поле вращающейся поляризации. Такие излучатели обладают рядом уникальных свойств, которые обеспечиваются подмагниченным ГР: излучение поля круговой поляризации; электрическая коммутация направления вращения, высокая частотная избирательность и магнитная перестройка центральной частоты излучения. Изменение направления вращения векторов поля происходит за счет переключения тока в электромагните. Смещение центральной частоты излучения можно произвести путем изменения тока в подмагничивающей катушке с проводом. В осевом направлении коэффициент эллиптичности поля излучения близок к единице. В работе рассматриваются два типа таких излучателей. Один обладает малыми размерами, другой большим коэффициентом излучения.

Статья в формате PDF

1197 KB

гиромагнитный резонатор

открытый объемный резонатор

конический рупор

поляризационная характеристика

коэффициент эллиптичности

СВЧ-концетратор

1. Солдатов А.А. Антенна // (Россия) А.С. №1818647 А1, класс H 01 Q 1/38, Опуб. 30.05.1993.

2. Солдатов А.А. Рупорная коническая антенна с подмагниченным гиромагнитным резонатором // Физика волновых процессов и радиотехнические системы. – 2006, – Т.4. – №9. – С. 70-72.

3. Анго А. Математика для электро- и радиоинженеров / Пер. с фран. – М.: Наука, 1967. – 780 с.

4. Осипов О.В., Плотников А.М., Салимова Н.Р. Использование эффекта азимутального рассеяния электромагнитных волн метаструктурой на основе элементов Телледжена в прикладных задачах электродинамики // Инфокоммуникационные технологии. – Т.10. – №1. – 2012. – С.8–15.

5. Сазонов Д. М. Антенны и устройства СВЧ. Учеб. для радиотехнич. спец. вузов. – М.: Высшая шк., 1988. – 432 с.

Одной из важнейших научных и практических задач на сегодняшний день является разработка и внедрение инновационных энергосберегающих технологий и систем на их основе. Высокой степенью актуальности в этой отрасли обладает задача по созданию структур, способных преобразовывать энергию электромагнитных волн, создаваемую при работе различных телекоммуникационных систем: сотовая связь GSM/DCS/UMTS/4G, беспроводных технологий Wi-Fi, Wi-MAX, систем эфирного телевидения и мн. др. В наш век информационных технологий энергия электромагнитного поля ВЧ в изобилии присутствует в окружающем пространстве, однако основная её часть не используется по непосредственному назначению (т.е. для работы самих систем передачи информации), а попросту расходуется вхолостую, рассеиваясь в различных объектах ландшафта. В работах [4] показано, что такая энергия может быть использована в полезных целях при построении автономных либо квазиавтономных систем вторичного электропитания радиоэлектронной аппаратуры, посредством концентрации такой энергии специальной структурой и последующего её эффективного преобразования в постоянный электрический ток.

Однако при проектировании структур-концентраторов, например подобных [4], разработчик может столкнуться с проблемой, связанной со сложностью измерения электрических характеристик таких структур: параметров матрицы рассеяния [S], характеристик направленности и поляризации. Эти трудности могут быть связаны с конструктивно-геометрическими особенностями СВЧ-концентраторов и высокими требованиями к передающей и приёмной антеннам измерителя: узкой угловой ДН при малой ширине линейной апертуры (малой геометрической площади раскрыва) антенны. Классические (в понимании теории антенн [5]) апертурные (и в некоторых случаях линейные) излучатели зачастую не способны дать подобную комбинацию характеристик, и в этом случае перед разработчиком встаёт задача спроектировать специальную антенную структуру, характеристики излучения которой удовлетворяют предъявляемым требованиям.

1. Модель кольца магнитного тока

На основе подмагниченного гиромагнитного резонатора (ГР) возможно создание управляемых частотно-независимых СВЧ антенн [1]. Несмотря на то, что ГР в таких антеннах является промежуточным звеном между возбуждающим СВЧ полем и открытым резонатором (ОР), основные свойства таких излучателей определяются подмагниченным ГР, а именно: создание вращающегося поля с эллиптической (а в осевом направлении с круговой) поляризацией; электрическая коммутация направления вращения поля; высокая частотная избирательность; магнитная перестройка частоты поля излучения. Наиболее компактная конструкция излучателя на основе ГР показана на рис. 1.

Принцип действия излучателей на основе подмагниченного ГР основан на следующих физических процессах: возбуждение полем фидерной линии процессии намагниченности сферического ГР; возбуждение в открытом резонаторе колебания квази – Е110 типа с вращающейся поляризацией через боковую поверхность ОР; излучение ОР во внешнее пространство электромагнитного поля с вращающейся поляризацией через боковую поверхность ОР.

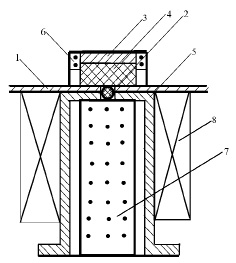
Рис. 1. Антенна на основе подмагниченного ГР: 1 – экран; 2 – ГР; 3 – стальной диск; 4 – плоский диэлектрический цилиндрический резонатор; 6 – магнитопровод; 7 – вкладыш из магнитодиэлектрика; 8 – подмагничивающая катушка с проводом

Математическая модель расчета поля излучения в дальней зоне представляет собой кольцо магнитного тока по боковой кромке ОР с плотностью:

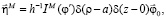
где .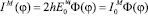

Исходным уравнением для нахождения поля излучения является уравнение Гельмгольца для магнитного потенциала:

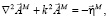
решением которого является следующее выражение

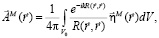(1)

выражения для составляющих электрического поля, найденные по формуле (1) [1, 2], записываются в виде:

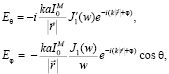(2)

откуда амплитудную характеристику диаграммы направленности можно представить следующей формулой:

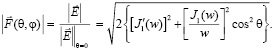(3)

В формуле (3) введены следующие обозначения: 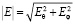, F(θ,,φ) – амплитудная диаграмма направленности; w =kasinθ; 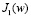– функция Бесселя первого рода, первого порядка.

Диаграмма направленности антенны, рассчитанная по формуле (3) в пространстве имеет вид, показанный на рис. 2.

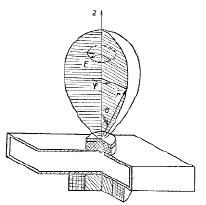
Рис. 2. Объемный вид амплитудной характеристики направленности

Предлагаемая антенна имеет большой интерес с точки зрения поляризационных характеристик, которые описываются нормированным вектором поляризации или векторной поляризационной характеристикой :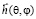

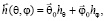
где 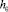и 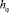поперечные составляющие вектора поляризации 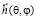в дальней зоне.

Эллипс поляризации, измеренный в дальней зоне, на конструкции антенны, изображенной на рис. 1, показан на рис. 3.

Составляющие вектора поляризации находятся по следующим формулам:

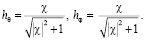
Здесь введен коэффициент эллиптичности

,

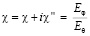Подставляя значения составляющих электрического поля по формулам (2), получим

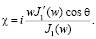
Зависимость модуля коэффициента эллиптичности от угла наблюдения θ в радианах представлена на рис. 4. Видно, что коэффициент эллиптичности достигает максимального значения в осевом направлении. Экспериментально показано, что коэффициент усиления максимален тоже в осевом направлении (θ =0).

На рис. 5 показано, как меняется коэффициент эллиптичности в пространстве от точки приема сигнала.

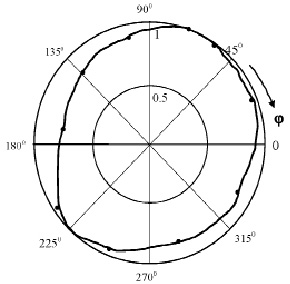
Рис. 3. Экспериментальная поляризационная характеристика антенны на основе ГР

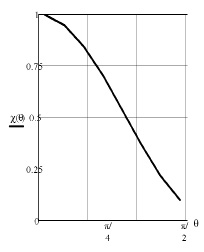
Рис. 4. Зависимость модуля коэффициента χ от угла наблюдения θ

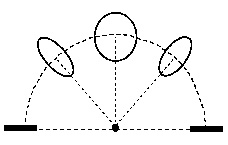
Рис. 5. Изменения эллипса излучения от угла наблюдения

Были проведены экспериментальные измерения параметров излучения (в том числе, коэффициента усиления и коэффициента эллиптичности) для антенны на основе подмагниченного ГР, показанной на рис. 1.

Измерения показали, что коэффициент усиления равен 1.6–1.8, КПД 0.7–0.8, коэффициент эллиптичности 0.9–0.95, полоса магнитной перестройки центральной частоты излучения 550–500 МГц. Рассмотренная антенна компактна, может использоваться как элемент антенной решетки и удобна для измерения характеристик СВЧ-концентраторов находящихся недалеко от излучателя.

2. Модель антенны как излучение вращающегося магнитного тока

Для того, чтобы получить излучатель со значительно большим коэффициентом излучения, рассмотрим антенну на основе конического рупора. Причем все уникальные свойства антенны рис.1, обусловленные подмагниченным ГР, присущи и рассматриваемому ниже излучателю. Коническая рупорная антенна на основе подмагниченного ГР, размещается на металлическом экране. Размеры экрана должны быть как минимум в 8 раз больше диаметра раскрыва рупора, чтобы избежать краевых эффектов.

Схема излучателя на экране показана на рис. 6. Расчет такой антенны нельзя проводить на основе модели кольца электрического тока, так как наведенный ток на экране ток будет иметь ту же величину и противоположное направление исходному току [2].

Примем за модель излучателя вращающийся ток в раскрыве антенны, как показано на рис 7.

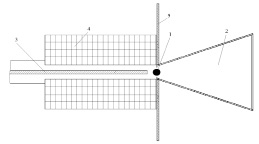
Рис. 6. Коническая антенна на основе ГР с экраном: 1 – ЖИГ сферической формы в отверстии; 2 – конический рупор; 3 – фидерная линия; 4 – электромагнит; 5 – металлический экран

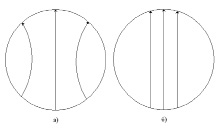
Рис. 7. Вращающиеся токи в раскрыве рупора

В дальней зоне антенну можно представить как вращающийся ток с постоянной плотностью j_м.

В правовращающейся системе ток можно представить в виде [1, 2]

,

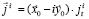где j_м – плотность магнитного тока.

Исходным уравнением для нахождения векторного магнитного потенциала 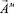является следующее уравнение:

.

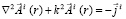Решение, которого определяется выражением [1, 2]:

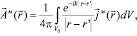(3)

где 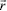– определяет вектор радиус точки наблюдения, 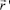– текущая координата интегрирования плоскости вращения тока (точки истока), V₀ – объем, в котором находится .

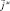Будем рассматривать дальнюю зону измерения, в этой зоне:

,

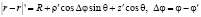где R – расстояние от начала координат до точки наблюдения.

Тогда формула (3) запишется в виде:

,

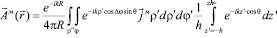или

,

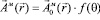где

,

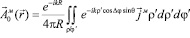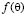– экранный множитель, учитывающий влияние металлического экрана, который находится по формуле:

.

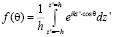Найдем потенциал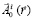

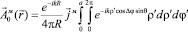(4)

Так как 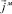постоянно, мы его вынесли за знак интеграла (4). Учитывая формулы [3], возьмем интеграл (4)

,

.

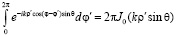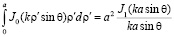Введем следующие обозначения: экранный множитель:

;

.

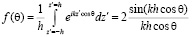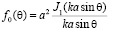В цилиндрической системе координат

.

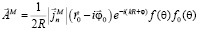Нетрудно записать выражения для составляющих магнитного потенциала в цилиндрической системе координат:

,

.

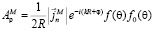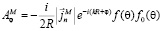Поскольку характеристики антенн, как правило, определяются в сферической системе координат, то запишем в этой системе выражение для вектора потенциала 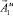. При переходе к сферической системе координат от полярной будут справедливы следующие формулы [3]:

.

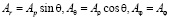И решение нашей задачи для вектора 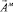в сферической системе координат запишется в следующем виде:

,

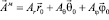где

,

.

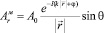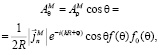
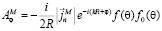Запишем выражение для составляющих электромагнитного поля 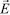и 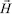в сферической системе координат. Для дальней зоны можно пренебречь слагаемыми, пропорциональными 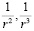и в результате получим следующие выражения для составляющих электромагнитного поля:

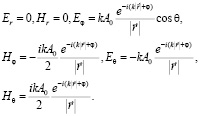
При нахождении этих формул использовались известные соотношения:

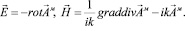
Рассмотрим амплитудную характеристику диаграммы направленности в дальней зоне

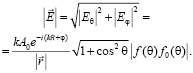
Максимальное значение 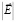имеет место при :

.

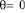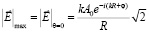Амплитудная диаграмма направленности 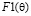находится по простой формуле:

.

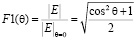И тогда к общему решению уравнения для 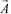прибавляется экранный множитель и окончательно получаем

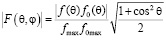, (5)

где

.

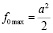3. Анализ полученных результатов и выводы

Результаты расчета по полученным формулам приведены ниже.

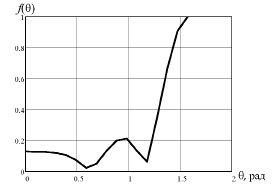
Рис. 8. Зависимость экранного множителя от угла θ

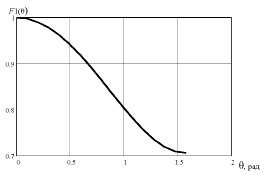
Рис. 9. Зависимость множителя 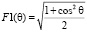от угла θ в декартовой системе координат.

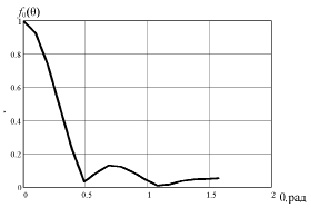
Рис. 10. Зависимость множителя 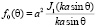от угла θ в декартовой системе координат

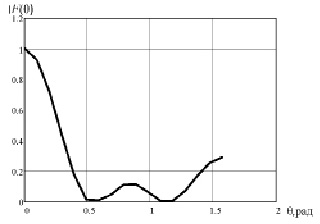
Рис. 11. ДН рупорной антенны на основе подмагниченного ГР с экраном в декартовой системе координат

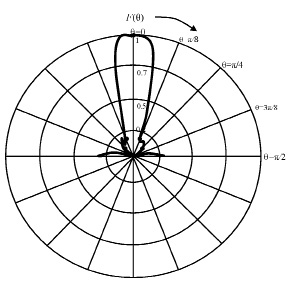
Рис. 12. ДН рупорной антенны на основе подмагниченного ГР с экраном в полярной системе координат

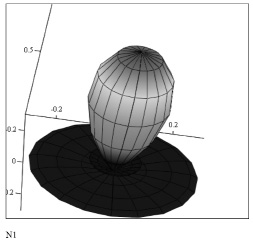
Рис. 13. Трехмерная ДН рупорной антенны на основе подмагниченного ГР с экраном в полярной системе координат

Как видно из рис. 11-13 диаграмма направленности (ДН) рупорной антенны на ГР с экраном близка к ДН рупорной антенны [2] и несколько уже, чем ДН рупора с ГР без экрана. В ДН появились боковые лепестки, интенсивность которых максимальна в направлении 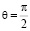и меньше трети главного лепестка. Появление боковых лепестков обусловлено вкладом экранного множителя (рис. 8). Коэффициент эллиптичности порядка 0.8. Коэффициент усиления существенно больше, чем антенны без экрана [5] и составляет порядка 30.

Рассмотренную рупорную антенну можно использовать для измерения поляризационных характеристик на значительно более дальнем расстоянии, чем антенны рис. 1. Рассмотренные излучатели можно применять, также, для создания измерителей поляризационных характеристик, поляризаторов и т.п.

Библиографическая ссылка