Характерным физическим явлением, сопровождающим промерзание тонкодисперсных грунтов (супесей, суглинков, глин) является их криогенное пучение. Данный процесс в природных условиях вызывает образование разнообразных форм рельефа – от мелких сезонных (возникающих в зимнее время) кочек и бугорков до многолетних бугров, иногда достигающих в высоту десятков метров. Пучение грунтов в основании зданий и сооружений может приводить к их деформациям вплоть до полного разрушения конструкций. Никакой другой криогенный процесс не был подвергнут столь всестороннему исследованию, как пучение грунта. Но, как это ни парадоксально, до сих пор имеются пробелы в объяснении физической сущности движущих сил данного процесса [2, стр. 121].
Постановка проблемы
Рассмотрим существо имеющейся проблемы. Согласно общепринятым представлениям, пучение грунта происходит вследствие увеличения его объема при промерзании. При этом характерным признаком пучения, является подъем поверхности промерзающего грунта. Возникает вопрос: почему наблюдается подъем, если наращивание толщины промерзающего слоя (движение фронта промерзания грунта) происходит в противоположном направлении. Объяснение этому дается в [1]: «В естественных условиях расширение грунта возможно лишь вверх, так как расширению в стороны препятствует, вообще говоря, такое же стремление к расширению боковых участков грунта, а расширению вниз – развивающееся с давлением сопротивление нижележащих слоев, тогда как перемещению вверх мешает лишь вес вышележащих слоев» (стр. 132). Таким образом, промерзающий слой как бы «отжимается» от нижележащей опоры, которой в природных условиях служит талый грунт. Подобный взгляд находит отражение в известном условии Маккея [10], согласно которому пучение наблюдается лишь в том случае, если сопротивление талого грунта сжатию Q превосходит сопротивление поднятию мерзлой толщи F:
Q > F (1)
В выражении (1) величина F складывается из давления от веса мерзлой толщи G и силы сопротивления мерзлого грунта деформирующим усилиям (изгибу, разрыву, сдвигу) U: F = G + U. Условие (1) раскрывает физическую сущность пучения как проявления действия третьего закона Ньютона, согласно которому перемещение любого материального тела (в нашем случае – промерзшего грунта) может происходить только в результате его силового взаимодействия с внешней средой (талым грунтом). Как следует из условия (1), для того, чтобы развивалось пучение, талый слой, подстилающий промерзающий грунт, должен обладать достаточной «жесткостью», превосходящей не только давление от веса мерзлого грунта G, но и его сопротивление деформирующим усилиям U.
Подобный механизм пучения оказывается не универсальным, если рассмотреть его в применении к двум различным типам промерзающих грунтовых систем – замкнутым и открытым. В замкнутых системах промерзающий изначально талый грунт со всех сторон отделен от внешней среды водонепроницаемой оболочкой. Характерным примером замкнутой системы в природе могут служить инъекционные бугры пучения, образующиеся, например, в процессе промерзания подозерных таликов [5]. Там водонепроницаемой оболочкой является мерзлый слой, окружающий промерзающий талый грунт, залегающий внутри бугра. В открытых системах замкнутая водонепроницаемая оболочка вокруг промерзающего грунта отсутствует. Примером открытой системы являются миграционные бугры пучения, которые формируются на промерзающих участках болот, сложенных тонкодисперсными талыми грунтами [7].
По характеру изменения соотношения между Q и F в процессе промерзания грунта существует принципиальная разница между этими типами систем. В замкнутых системах некуда отжиматься избытку воды, образующемуся при фазовом переходе «вода-лед», что приводит к возрастанию давления в талом грунте, причем развивающихся при этом сил может вполне хватить для деформации мерзлой кровли или даже ее разрыва с излиянием жидкой массы грунта на поверхность. Таким образом, в замкнутых системах условие (1) развития пучения выполняется. Сопротивление сжатию при промерзании обеспечивается не только в замкнутых природных системах, но также при исследовании пучения грунта в лабораторных условиях. В лаборатории промерзающий грунт помещается в сосуд с жесткими боковыми стенками и опирается на практически несжимаемый песок, из которого поступает вода к фронту промерзания. Поэтому расширение промерзшего грунта вследствие накопления в нем льда может реализоваться только вверх. Следовательно, в лаборатории по существу изучаются замкнутые системы. Отметим также, что в замкнутых системах природа силы пучения связана с давлением растущих ледяных кристаллов, что согласуется с традиционными представлениями. При этом сколь велико ни было бы давление льда, его силовой эффект не может превзойти силу сопротивления талого грунта сжатию (или же прочность водонепроницаемой оболочки), т.е., в соответствии с третьим законом Ньютона, силу реакции опоры.
В открытых системах избыток воды свободно перераспределяется в талом грунте. Поэтому там нет физических предпосылок для нарастания давления в подстилающем промерзающий слой талом грунте. Напротив, по мере увеличения мощности мерзлого слоя, возможность развития пучения, с точки зрения необходимости соблюдения условия (1), снижается. Сказанное иллюстрирует рис. 1, отражающий принципиальную динамику величин Q и F в разных системах по мере их промерзания. Справа от точки пересечения графиков Q и F в замкнутых системах пучение начинается, а открытых должно прекратиться.
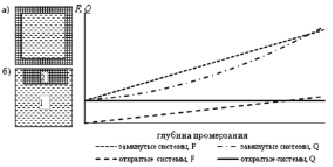
Рис. 1. Динамика величин Q и F в замкнутых(а) и открытых(б) грунтовых системах. 1 – талый грунт, 2 – мерзлый грунт
Отсутствие нарастания давления в талом грунте, промерзающем в условиях открытой системы, подтверждается экспериментальными данными из [3]. Измеренное давление в талой зоне не превышало 0,03 МПа, причем на участках, примыкающих к фронту промерзания, оно падало практически до 0. Анализируя полученные данные, В.О. Орлов приходит к выводу, что «…слой талого грунта ниже фронта промерзания нельзя рассматривать как некоторую зону пластических деформаций, которая находится под равномерно распределенной нагрузкой, являющейся функцией мощности промерзающего слоя» [3, стр. 124].
Таким образом, как общетеоретические соображения, так и фактические данные показывают, что в открытых грунтовых системах условие (1) развития криогенного пучения не «работает». Какая же сила заставляет здесь мерзлый грунт подниматься вверх?
Литостатический механизм криогенного пучения открытых грунтовых систем
Попробуем найти ответ на поставленный вопрос, анализируя изменение при промерзании такого свойства грунта, как плотность. Характерным физическим явлением, сопровождающим промерзание тонкодисперсных грунтов (супесей, суглинков, глин), способных к пучению, является их разуплотнение при переходе в мерзлое состояние. Существуют, по крайней мере, три возможные причины разуплотнения. Во-первых, удаление из порового пространства промерзшего грунта избытка воды, равного разности между увеличением объема поровой воды при переходе ее в лед и объемом части пор, незаполненной водой. Во-вторых, в мерзлом грунте могут образовываться микро и макро пустоты, уменьшающие его плотность [1]. Третьей причиной (несравненно более эффективной по сравнению с двумя предыдущими) является формирование миграционного льда, доля которого в объеме мерзлой породы может составлять десятки процентов [7]. При этом такой же порядок имеет разница плотностей талого и мерзлого грунта.
Таким образом, при промерзании тонкодисперсного грунта в условиях открытой системы образуется мерзлое тело с меньшей плотностью по сравнению с окружающим это тело талым грунтом. Можно предположить, что при этом возникает выталкивающая сила, стремящаяся вытеснить это мерзлое тело из талого грунта вверх. Такое предположение не кажется невероятным, если учесть, что в природе разность плотностей горных пород вызывает, например, явление диапиризма [9].
Сила, выталкивающая мерзлый грунт из талого, по сути является архимедовой силой, действие которой в водной и воздушной среде общеизвестно и, например, учитывается при проектировании судов и воздухоплавательных аппаратов. Что же касается грунтов, то практический учет в них архимедовой силы автором статьи нигде встречен не был, за исключением нормативного документа, регламентирующего строительство трубопроводов [8]. Там в примечании к п. 8.14 говорится о том, что «при проектировании трубопроводов на участках переходов, сложенных грунтами, которые могут перейти в жидко-пластическое состояние, при определении выталкивающей силы следует вместо плотности воды принимать плотность разжиженного грунта, определяемую по данным изысканий» (т.е. фактически учитывать в расчете архимедову силу в грунтах). Механизм криогенного пучения, связанный с воздействием архимедовой силы, с учетом физических свойств среды, в которой этот механизм проявляется, можно назвать «литостатическим».
Основные положения литостатической концепции
1. В природе зимнее промерзание грунта характеризуется пространственно-временной неоднородностью, обусловленной неоднородностью факторов, определяющих условия промерзания (главным образом, снежного и почвенно-растительного покровов). Вследствие этого в начальный период промерзания образуются отдельные мерзлые массивы, окруженные талым грунтом и промерзающие по типу открытой системы (без нарастания давления в талой толще).
2. На массивы, формирующиеся в тонкодисперсных (глинах, суглинках, супесях) влажных грунтах действует выталкивающая (архимедова) сила Fв, равная:
Fв = gρтV (2)
где ρт – плотность талого грунта, V – объем мерзлого массива, g – ускорение земного тяготения.
3. Если плотность мерзлого грунта ρм меньше плотности талого ρт, то выталкивающая сила может вызвать всплытие мерзлого массива из талого грунта под действием направленной вверх части выталкивающей силы, равной разности Fв и веса мерзлого массива G. Эту разность можно обозначить как движущую силу пучения Fдв:
Fдв = Fв – G = gρтV – gρмV = gV(ρт – ρм). (3)
4. Всплытию мерзлого массива может препятствовать сопротивление сдвигу по его боковой поверхности Fс, а также дополнительная внешняя нагрузка на массив P. Отсюда условием всплытия, т.е. начала пучения промерзающего грунта, является выполнение неравенства:
Fдв > Fc + P. (4)
Это неравенство может начать выполняться по мере дальнейшего промерзания массива, возрастании его объема V и увеличения Fдв в соответствии с формулой (3). Дополнительное воздействие может оказать возрастание льдистости массива, приводящее к уменьшению его плотности ρм.
5. С момента начала всплытия (пучения) объем мерзлого массива V разделяется на две части: вытолкнутую из талого грунта (надземную) Vн и погруженную в талый грунт (подземную) Vп (V = Vн + Vп). При этом по мере дальнейшего промерзания система «мерзлый массив – талый грунт» в каждый момент времени стремится к положению статического равновесия, соответствующего условию:
Fв = G + Fc + P, (5)
где Fв – выталкивающая (архимедова) сила, действующая на подземную часть мерзлого массива Vп).
Равенство (5) можно привести к следующему виду:
g(ρт – ρм)Vп = gρмVн + Fc + P. (6)
Левая часть равенства (6) есть Fдв, действующая на подземную часть мерзлого массива, а произведение ρмgVн – вес надземной части мерзлого массива Gн. Пока идет промерзание, постоянно возрастают объемы подземной Vп и надземной Vн частей массива, что соответствуют все новым положениям статического равновесия и постоянному выпучиванию мерзлого массива. При этом массив, вследствие своей инерции, всегда несколько отстает от положения статического равновесия. Но, как только промерзание заканчивается, это положение достигается.
6. Если с какого-то момента воспрепятствовать подъему мерзлого массива (пучению), а промерзание будет продолжаться, то статическое равновесие нарушится, что соответствует нарушению равенства (6). Правая часть его остается постоянной, а левая (движущая сила) растет пропорционально увеличению Vп. Этот рост не компенсируется возрастанием веса надземной части массива в формуле (6), поскольку массив «застопорен». Силу, которая стремится смещать вверх «застопоренный» массив, можно обозначить как силу пучения Fпуч, которая рассчитывается по формуле:
Fпуч = g(ρт – ρм)V – Fc, (7)
где ΔV – приращение объема мерзлой части массива или (что то же самое) всего массива с момента его остановки.
7. В зависимости от конфигурации мерзлого массива, можно определить высоту его вытолкнутой части (величину пучения) hр, соответствующую условию статического равновесия. Для наглядности приведем рис. 2, на котором показан мерзлый массив в форме цилиндра в положении статического равновесия при отсутствии нагрузки (P = 0)
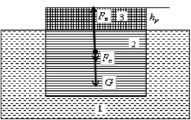
Рис. 2. Мерзлый массив в положении статического равновесия и действующие на него силы. Условные обозначения: 1 – талый грунт; 2 – подземная часть мерзлого массива; 3 – надземная часть мерзлого массива; G – вес надземной части мерзлого массива; Fс – сопротивление сдвигу; Fв – архимедова сила (Fв = Gн + Fс)
Если массив имеет форму цилиндра (в том числе и неправильного), или параллепипеда, то выражение (6) записывается в виде:
g(ρт – ρм)S(H – hp) = gρтShp + Fc + P, (8)
где S – площадь основания массива, H – толщина массива (глубина промерзания), Отсюда, при отсутствии внешней нагрузки на мерзлый массив (P = 0):
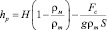(9)
При наличии нагрузки:
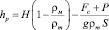(10)
Параметры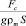 
и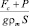 
в формулах (9) и (10) равны возможному уменьшению высоты выпучивания мерзлого массива (Δhp) за счет воздействия силы сопротивления сдвигу и нагрузки на массив.
8. Рассмотренные выше геометрические параметры мерзлого массива в форме цилиндра или параллепипеда – H, S можно использовать при расчете силы пучения Fпуч. Для этого в формуле (7) приращение объема заменяется на произведение площади на приращение высоты ΔH, причем ΔH равно глубине промерзания с момента остановки подъема массива (пучения). Отсюда:
Fпуч = g(ρт – ρм)SH – Fc. (11)
Материалы и методы исследования
Для доказательства справедливости литостатической концепции автором были выполнены опыты, при которых сопоставлялись экспериментальные и расчетные данные. Сначала была проведена серия опытов со специально изготовленными мерзлыми цилиндрами с целью проверки справедливости формул (9) и (10). Затем был выполнен опыт, в ходе которого измерялась сила выпучивания промерзающего массива неправильной формы из талого грунта при невозможности всплытия с самого начала промерзания, т.е. проверялась справедливость формулы (7). Рассмотрим эти опыты.
Опыты с мерзлыми цилиндрами
Если в талом грунте образуется мерзлый массив в форме, например, цилиндра, то он должен всплывать, причем высота этого всплытия в момент его окончания (прекращения промерзания) должна примерно равняться значениям hр, вычисленным по формуле (9) для ненагруженного цилиндра, или по формуле (10) для цилиндра с внешней нагрузкой.
Возможны два варианта выполнения указанных опытов в лабораторных условиях. Первый – замораживать с поверхности некоторый участок талого грунта, добиваясь создания внутри него мерзлого тела и определять высоту всплытия этого тела. Но, помимо технических сложностей, нет гарантии получения мерзлого тела правильной (цилиндрической) формы, позволяющей установить точные значения параметров, входящих в формулы (9) и (10). Второй вариант – изготовление мерзлых цилиндров с наперед заданными параметрами, погружение этих цилиндров заподлицо в талый грунт и наблюдение за их последующим всплытием. При этом высота цилиндров моделирует глубину промерзания грунта H (чем больше высота, тем больше H).
Были выполнены два опыта с погружением мерзлых цилиндров в талый грунт. Первый опыт проведен для проверки справедливости формулы (9), т.е. при отсутствии внешней нагрузки на мерзлый массив (P = 0), с двумя одинаковыми (по форме и размеру) цилиндрами – ледогрунтовым и ледяным, имеющими следующие параметры: высота 5,5 см, диаметр 10,5 см, площадь основания 87 см2, объем 476 см3. Цилиндры эти показаны на рис. 3, а. Ледогрунтовый цилиндр состоял из двух ледяных и трех грунтовых прослоек толщиной примерно по 1 см. Ледяной цилиндр весил 4,3 Н, т.е. имел плотность (ρм) 0,92 г/см3. Ледогрунтовый цилиндр имел вес 6,5 Н, и, соответственно, плотность (ρм) 1,4 г/см3.
Цилиндры полностью (заподлицо) погружались в талый грунт с температурой около 0 °С; такой же была температура наружного воздуха. Грунт был подмосковный суглинок, гранулометрический состав и пластичность которого приведены в табл. 1. Из этого же грунта были изготовлены грунтовые прослойки ледогрунтового цилиндра. Влажность талого грунта в опыте была 0,31, т. е., в соответствии со своими пластическими свойствами (см. табл. 1), грунт имел мягкопластичную консистенцию [6]. Плотность грунта ρт составляла 1.87 г/см3.
Таблица 1
Характеристика грунта, использованного в опытах
|
Содержание фракций, % |
Пластичность |
||||||||
|
песок |
пыль |
глина |
Влажность пределов, % |
Число |
|||||
|
05-0.25 |
0.25-0.1 |
0.1-0.05 |
0.05-0.01 |
0.01-0.005 |
0.005-0.002 |
< 0.002 |
верхнего |
нижнего |
|
|
3 |
10 |
32 |
39 |
5 |
5 |
6 |
35 |
21 |
14 |
После погружения цилиндры были предоставлены сами себе. Практически сразу началось их всплытие, которое прекратилось через несколько минут. Ледогрунтовый цилиндр всплыл на 1,2 см, а ледяной цилиндр на 2,8 см (см. рис. 3, б). По формуле (9) была рассчитана теоретическая высота всплытия цилиндров hр при Fс = 0, которая для ледогрунтового цилиндра составила 1,4 см, а для ледяного 2,8 см.
Рис. 3. Опыт с мерзлыми цилиндрами при отсутствии нагрузки: а) – внешний вид цилиндров, б) – характер всплытия цилиндров
Очевидно, у ледяного цилиндра сила сопротивления сдвигу по талому грунту Fс была настолько мала, что возможное различие фактической и расчетной высот всплытия Δhp не превышало точности измерения в условиях опыта (погрешность 0,5 мм). У ледогрунтового цилиндра Δhp составила около 2 мм, что можно объяснить влиянием Fс, величину которой можно рассчитать, учитывая формулу (9), по формуле:
Fс = gΔhpρтS. (12)
В данном случае Δhp = 0,2 см, S = 87 см2, ρт = 1,87 г/см3. Отсюда Fс равна около 0,33 Н. Архимедова сила в положении статического равновесия (действующая на подземную часть ледогрунтового цилиндра), рассчитанная по формуле (2), равна 6,5 Н. Таким образом, Fс составила около 5 % от архимедовой силы. В случае же ледяного цилиндра Fс можно было пренебречь.
Второй опыт выполнялся в условиях переменной внешней нагрузки на поверхность ледяного цилиндра, имеющего следующие параметры: диаметр 9,5 см, высота 6,1 см, объем 432 см3, вес 4 Н, плотность 0,92 г/см3. На поверхность цилиндра, накрытую бумажным кружком, был помещен груз, состоящей из металлической пластинки массой 113 г и комплектом разновесок для лабораторных весов массой 200 г. Таким образом, общая нагрузка составила (при массе 313 г) 3,07 H. Цилиндр вместе с грузом был погружен заподлицо в талый грунт (тот же самый, что и в первом опыте) с влажностью 0,33 (т.е. текучепластичной консистенции) и плотностью 1,86 г/см3 и после этого предоставлен сам себе. После прекращения всплытия цилиндра была замерена его высота, а затем нагрузка была уменьшена до 200 г (1,96 H). Вследствие уменьшения нагрузки вновь началось всплытие. В процессе опыта такая операция была проделана при шести ступенях нагрузки (вплоть до полного ее удаления). Моменты окончания всплытия при четырех ступенях нагрузки (3,07 Н; 1,96 Н; 0,98 Н; без нагрузки) зафиксированы на разных фрагментах рис. 4.
Рис. 4. Опыт с нагруженным ледяным цилиндром. Характер всплытия при нагрузке: а) – 3,07 Н; б) – 1,96 Н; в) – 0,98 Н; г) – без нагрузки
Результаты опыта представлены в табл. 2, где расчетная высота всплытия определялась по формуле (10) при условии, что Fс = 0. Как мы видим, теоретическая и фактическая высоты всплытия в первых трех строках табл. 2 почти равны, а в последних трех практически совпадают.
Таблица 2
Результаты опыта с переменной нагрузкой на поверхность цилиндра
|
Время от начала опыты, мин. |
Масса, г |
Нагрузка, Н |
Высота всплытия, см |
|
|
фактическая |
расчетная |
|||
|
30 |
313,0 |
3,07 |
0,6 |
0,7 |
|
80 |
200,0 |
1,96 |
1,5 |
1,6 |
|
120 |
150,0 |
1,47 |
1,9 |
2,0 |
|
133 |
100,0 |
0,98 |
2,3 |
2,3 |
|
155 |
50,0 |
0,49 |
2,7 |
2,7 |
|
200 |
0,0 |
0 |
3,1 |
3,1 |
Измерение силы выпучивания мерзлого массива
Основным условием проведения эксперимента было обеспечить возможность образования мерзлого массива, окруженного со всех сторон талым грунтом, промерзающим сверху. Поскольку ранее такие опыты никем не выполнялись, пришлось создать оригинальную установку, аналогов которой не было. Конструкция установки представлена на рис. 5, А.
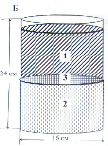
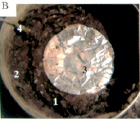
Рис. 5. Опыт по измерению силы пучения в условиях открытой системы. А – общий вид установки: 1 – контейнер с грунтами; 2 – ведро с водой; 3 – кольцо теплоизоляции; 4 – кружок из фольги; 5 – нагревательная лента ЭНГЛ-1; 6 –коромысло; 7 – упор; 8 – платформенные весы; 9 – температурное реле ТР-35М; 10 – предохранитель; 11 – контейнер – подставка для весов; 12 – датчик температуры. Б – контейнер с грунтами: 1 – суглинок пылеватый; 2 – песок кварцевый, тонкозернистый; 3 – сетка. В – поверхность грунта в конце опыта: 1 – мерзлый грунт, 2 – талый грунт, 3 – кружок из фольги, 4 – датчик температурного реле. Г – извлеченный мерзлый грунт
В процессе промерзания грунта, помещенного в контейнер 1, поддерживалась его температура в интервале от 0 до 1 °С, что обеспечивалось частью установки, состоящей из ведра с водой 2, нагревательной ленты ЭНГЛ-1 (общей длиной 3 м) 5, намотанной на контейнер, температурного реле ТР-35М (с гистерезисом 1 °С) 9 с датчиком температуры 12, помещенным в приповерхностную часть грунта вблизи стенки контейнера, кольца теплоизоляции 3 над поверхностью грунта вдоль внутренней стенки контейнера. Восприятие и передача усилия со стороны поверхности грунта при его промерзании осуществлялись с помощью коромысла 6, жестко закрепленного на подставке всей установки, с двумя упорами 7, один из которых опирался на кружок из фольги 4, помещенный на поверхность грунта, а другой – на платформу весов 8, расположенных на металлическом контейнере-подставке 11. Эти весы (предел измерения 500 г, цена деления 0,1 г) фиксировали силу пучения.
В качестве опытного грунта использовался подмосковный суглинок, характеристика которого приведена в табл. 1. Суглинок занимал верхнюю половину контейнера (рис. 5, Б) и отделялся сетчатой перегородкой от тонкозернистого кварцевого песка, заполнявшего нижнюю половину контейнера. Сетка между песком и суглинком была помещена с целью исключения их перемешивания, которое выполнялось с суглинком перед началом опыта для достижения равномерной консистенции грунта. В нижней части контейнера была специально нарушена герметичность конструкционного шва, благодаря чему вода из ведра полностью насыщала кварцевый песок и из него поступала в суглинок. При подготовке опыта вода в ведро доливалась до тех пор, пока ее уровень не совпадал с дневной поверхностью суглинка.
Опыт выполнялся в открытом помещении, при температуре наружного воздуха – 16 ÷ −19 °С. Перед началом опыта вся установка в течение двух суток выдерживалась на морозе, при установленной на температурном реле температуре 0 °С. Для предотвращения промерзания грунта сверху в это время поверхность контейнера накрывалась бумажным листом, чего оказалось достаточно. В воде в ведре постоянно шли фазовые переходы воды в лед и обратно, т.е. температура вокруг контейнера с грунтом колебалась около нулевого значения. Температура суглинка вблизи его поверхности около стенки контейнера, в соответствии с заданным на реле режимом, колебалась в интервале от 0 до 1 °С.
Выполнить эксперимент с соблюдением всех необходимых условий технически было сложно. Самое главное было добиться того, чтобы исключить смерзание образующегося мерзлого грунта со стенкой контейнера. Однако уже в самом начале опыта между мерзлым грунтом и стенкой то тут, то там возникала мерзлая «перемычка» (даже несмотря на наличие кольца из теплоизоляции) до окончания образовании приемлемого для исследования объема мерзлого грунта. После серии из 7 неудачных попыток удалось добиться нужного результата.
Результат успешного опыта представлен в табл. 3.
Таблица 3
Результаты опыта по измерению силы пучения в условиях открытой системы
|
Время |
Температура воздуха, °С |
Показания весов, г |
Сила пучения, Н |
|
15 час. 30 мин. |
– 15 |
0 |
0 |
|
17 час. 15 мин. |
– 16 |
28,9 |
0,283 |
|
18 час. 00 мин. |
– 16 |
36,4 |
0,356 |
|
19 час. 00 мин. |
– 17 |
58,1 |
0,57 |
Отсчет времени начался с момента начала промерзания грунта под кружком из фольги, что фиксировалось на ощупь. В ходе опыта возрастал объем мерзлого грунта по мере его промерзания. Поскольку промерзающий массив не мог перемещаться вверх (препятствовала жесткость конструкции весов), то вместе с его объемом росла и сила пучения.
Опыт был прекращен вследствие опасения, что часть промерзающего грунта может примерзнуть в стенке контейнера и условия выполнения эксперимента нарушатся. В конце опыта упор коромысла был снят с поверхности мерзлого грунта, которая после этого практически сразу испытала поднятие относительно поверхности талого грунта (пучение), составившее около 4 мм. При этом было достигнуто положение статического равновесия. Вид поверхности грунта в конце опыта приведен на рис. 5, В. Затем мерзлый грунт был извлечен из талого. На это были затрачены усилия, которые привели к отделению от мерзлого образца нескольких фрагментов по плоскостям ледяных прослоек с толщиной в десятые доли мм. Извлеченный мерзлый грунт показан на рис. 5, Г.
Вес извлеченного мерзлого грунта составил 232,5 г, а объем 161 см3, что дает плотность ρм = 1,44 г/см3. Результаты опробования грунта после опыта приведены в табл. 4.
Таблица 4
Результаты опробования суглинистого грунта
|
№ бюкса |
Вес бюкса, г |
Объем бюкса, см3 |
Вес бюкса с талым грунтом, г |
Вес бюкса с мерзлым грунтом, г |
Вес бюкса с сухим грунтом, г |
Влажность талого грунта |
Влажность мерзлого грунта |
Плотность талого грунта ρт, г/см3 |
|
113 |
15,0 |
63,4 |
130,4 |
– |
95,7 |
0,33 |
1,82 |
|
|
348 |
15,1 |
– |
– |
67,8 |
45,3 |
– |
0,75 |
– |
По формуле (7) при Fс = 0 была рассчитана сила пучения Fпуч в конце опыта (при ΔV = 161 см3, ρт = 1,82 г/см3, ρм = 1,44 г/см3), которая оказалась равной 0,60 H. Это больше конечного показания весов, равного 0,57 H (см. табл. 3) всего лишь на 0,03 H или на 5 %. Вероятно, данное отличие связано с точностью определения экспериментальных параметров, а также с силой сопротивления сдвигу боковой поверхности мерзлого грунта по контакту с талым грунтом Fс, которая при расчете не учитывалась. Таким образом, результаты выполненного эксперимента, также как и опытов с цилиндрами, подтверждают возможность выпучивания мерзлого массива из талого грунта под действием архимедовой силы.
Эксперимент В.О. Орлова
Представление о выпучивании цельного мерзлого массива, который увлекает вверх вместе с собой все находящиеся на нем предметы, было высказано еще в [1], где это было использовано для объяснения одинакового выпучивания столбов с различной засыпкой. К сожалению, эти воззрения не получили дальнейшего развития в трудах специалистов, исследующих выпучивание фундаментов, что, в частности, не позволило правильно интерпретировать результаты некоторых экспериментов. Для примера, рассмотрим экспериментальные данные В.О. Орлова, полученные при изучении нормальных сил морозного пучения тонкодисперсных грунтов вблизи г. Игарка в 1958 г. на опытной площадке № 2 [3].
На площадке в грунт на глубину 0,62 м закапывалась круглая мессдоза с площадью рабочей пластины 200 см2. которая должна была воспринимать усилие со стороны промерзающего грунта [3]. Схема установки мессдозы в грунт показана на рис. 6, взятом из [3, рис. 50].
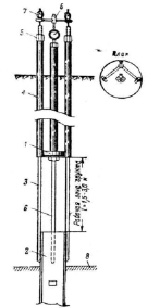
Рис. 6. Схема установки для определения нормальных сил пучения: 1- мессдоза; 2 – анкер, заложенный в многолетнемерзлые грунты; 3 – стальные стержни диаметром 19 мм; 4 – трубки диаметром 25 мм, удерживающие мессдозу в неподвижном положении посредством гаек 5, обмотанные марлей, пропитанной солидолом; 5 – гайки высотой 80 мм; 6 – стержень для установки индикаторов, фиксирующих упругие деформации стержней; 7 – индикатор; 8 – поверхность многолетнемерзлых грунтов
Опытная площадка очищалась от почвенно-растительного и снежного покровов, что вызывало ее активное промерзание. В то же время вокруг площадки был талик, поскольку туда с нее сбрасывался снег, оказывающий отепляющее воздействие на грунты. По сути, на опытной площадке № 2 формировался мерзлый массив с постепенно возрастающей (по мере промерзания) мощностью, окруженный со всех сторон талым грунтом.
Попробуем рассчитать по формуле (11) величину силы пучения Fпуч при тех значениях входящих в эту формулу параметров, которые соответствовали условиям проведения В.О. Орловым своего эксперимента.
Площадка № 2 была заложена на участке, сложенном с поверхности талыми пылеватыми суглинками с влажностью 0,30 – 0,36, с глубины 1,7 м находящимися в многолетнемерзлом состоянии. Размеры площадки были 11х12 м [4], т.е. ее площадь составляла 132 м2. К сожалению, в процессе эксперимента не выполнялись определения плотности талого и мерзлого грунтов, но имеются данные по влажности, которые позволяют получить хотя бы ориентировочные значения. Примем для талых суглинков площадки № 2 среднее значение плотности, для суглинка, использованного в обоих лабораторных экспериментах (см. выше) с влажностью 0.33, т.е. ρт = 1.85 г/см3. Далее перейдем к плотности мерзлого грунта. Эту плотность можно определить с допущением (справедливым для нашего случая) полного заполнения льдом и незамерзшей водой промежутков между минеральными частицами, что дает расчетную формулу:
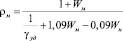, (13)
где γуд – удельный вес минеральных частиц грунта, Wм – влажность мерзлого грунта, Wн – влажность за счет незамерзшей воды. Принимая γуд равным 2,7 г/см3 (среднее значение для глинистых грунтов), получаем:
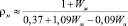. (14)
Средняя величина влажности мерзлого грунта, по данным обследования площадок №№ 4, 5 [4], сложенных суглинками, сходными с грунтами площадки № 2, равна 0,43. Количество незамерзшей воды принимаем по данным из [6, табл. 3] для суглинков при температуре − 4,5 ÷ − 5 °С, т.е. Wн = 0,05. При таких параметрах расчет по формуле (14) дает величину ρм , равную 1,71 г/см3.
Рассмотрим приведенную ниже табл. 5, в которой в трех первых колонках помещены данные, относящиеся к площадке № 2 и взятые из [4, табл. 15]. В последней колонке табл. 5 находятся значения силы пучения Fпуч, рассчитанные по формуле (11) при Fс = 0. Исходные параметры для расчета, в соответствии с вышеизложенным, следующие: S = 132 м2, ρт = 1,85 т/м3, ρм = 1,71 т/м3, ΔH равно мощности мерзлого слоя под мессдозой (см первую колонку табл. 5).
Таблица 5
Фактические и расчетные значения силы взаимодействия мерзлого массива с мессдозой
|
Мощность мерзлого слоя под мессдозой, м |
Давление грунта под подошвой мессдозы, МПа |
Фактическая сила (по показаниям индикатора), КН |
Расчетная сила пучения Fпуч, КН |
Примечание |
|
0 |
0 |
0 |
0 |
Стадия 1 |
|
0,16 |
0,17 |
3,3 |
29,0 |
Стадия 2 |
|
0,2 |
0,28 |
5,5 |
38,8 |
|
|
0,24 |
0,60 |
11,8 |
46,6 |
|
|
0,3 |
2,05 |
40,2 |
58,2 |
|
|
0,36 |
3,52 |
69,0 |
69,9 |
Стадия 3 |
|
0,61 |
5,6 |
109,8 |
118,4 |
Чтобы правильно интерпретировать данные, приведенные в табл. 5, рассмотрим процесс эксперимента В.О. Орлова с теоретических позиций, изложенных в разделе 3. Для большей ясности целесообразно обратиться к рис. 6.
В процессе взаимодействия мерзлого массива с конструкцией, включающей в себя мессдозу (рис. 6), можно выделить три стадии. На первой стадии подошва мерзлого массива не достигла еще мессдозы 1 на рис. 6, а сам он, по мере возрастания его мощности, испытывал свободный подъем и в каждый момент времени был близок к состоянию статического равновесия. При этом фактическая и расчетная силы равнялись 0.
На второй стадии нижняя граница мерзлого массива достигла мессдозы, после чего началось все возрастающее промерзание грунта под мессдозой, глубина которого показана в левом столбце табл. 5. Пока температура и, соответственно, прочность промерзшего слоя позволяла, происходил сдвиг мерзлого массива относительно его части, находящейся под подошвой мессдозы. При этом мерзлый массив вокруг мессдозы перемещался вверх со скоростью сдвига, гораздо меньшей по сравнению со скоростью в условиях свободного подъема массива (без контакта с тормозящей его мессдозой). Под самой же мессдозой участок массива мог смещаться всего лишь на величину деформации рабочей пластины мессдозы, фиксируемой индикатором 7 на рис. 6. На рис. 7 отображен характер деформации грунта под мессдозой установки № 111 [3, фрагмент рис. 55]. Стрелками показано (автором настоящей статьи) ориентировочное положение поверхности сдвига. Грунт под мессдозой на рис. 7 оказался в напряженно-деформированном состоянии и местами раскалывался на отдельные фрагменты, на границах которых, а также в зоне сдвига образовывались ледяные шлиры, отображенные на фотографии темным цветом.
Вторая стадия соответствует данным табл. 5 при глубине промерзания под подошвой мессдозы до 0,30 м включительно. На второй стадии расходуется лишь часть силы пучения, необходимая для преодоления сопротивления сдвигу. При таких условиях величина деформации платформы мессдозы определялась усилием для преодоления этого сопротивления, которое меньше величины Fпуч, что объясняет несовпадение в табл. 5 расчетной и фактической силы на второй стадии. При этом, вследствие постепенного понижения температуры мерзлого грунта и соответствующего его упрочнения сопротивление сдвигу возрастало, что отразилось в росте фактической силы (см. табл. 5).
Третья стадия началась, когда прочность мерзлого слоя под мессдозой (вследствие понижения его температуры) возросла настолько, что дальнейший сдвиг стал невозможным и массив оказался «застопоренным». В табл. 5 первые данные, относящиеся к третьей стадии, соответствуют глубине промерзания под подошвой мессдозы около 0,36 м. По мере промерзания неподвижного массива и возрастания его мощности, он все более «отдалялся» от положения статического равновесия, вследствие чего постоянно возрастала Fпуч. Поскольку мессдоза вместе с массивом (будучи в него вморожена) составляла единое целое, то деформация ее пластины, передаваемая на индикатор, соответствовала величине Fпуч. Это нашло отражение в близости силы Fпуч, рассчитанной по формуле (11) и фактической силы в табл. 5, начиная с глубины промерзания под подошвой мессдозы 0,36 м. В последней строке табл. 5 расчетная сила превышает фактическую почти на 9 %, что можно объяснить исключением из расчета силы сопротивления сдвигу по боковой поверхности всего массива Fс, которая росла по мере промерзания в соответствии с увеличением площади боковой поверхности. Тем не менее, приведенные данные с очевидностью свидетельствую в пользу литостатического механизма пучения на площадке № 2.
Интересно, что на 3 стадии эксперимента В.О. Орлова площадь рабочей пластины мессдозы не оказывала влияния на величину фактической силы, поскольку мессдоза, будучи вморожена в мерзлый массив, составляла с ним единое целое, т.е. измерялась сила выпучивания всего массива. Поэтому так называемое «давление нормальных сил пучения», (вторая колонка табл. 5), определенное В.О. Орловым как частное от деления измеренной силы на площадь рабочей пластины мессдозы (200 см2) не имело физического смысла. Если бы площадь пластины мессдозы была, скажем, не 200 см2, а 400 см2, то величина давления нормальных сил пучения (при тех же самых мерзлотно-грунтовых и температурных условиях проведения эксперимента!) получилась бы у В.О. Орлова вдвое меньше. А ведь эта величина, по своей сути (как, очевидно и предполагалось экспериментатором), никоим образом не должна зависеть от выбора размера мессдозы. Отметим также, что и на второй стадии эксперимента (стадия сдвига) данные, полученные В.О. Орловым, (см. вторую колонку табл. 5) не являются давлением нормальных сил пучения, а представляют собой усилие сдвига, деленное на площадь мессдозы.
Рис. 7. Характер деформации грунта под мессдозой установки № 111
Результаты исследования и их обсуждение
Таким образом, как результаты представленных выше лабораторных опытов автора, так и полученные В.О. Орловым экспериментальные данные доказывают возникновение архимедовой силы в тонкодисперсных грунтах при их промерзании в условиях открытой системы. С помощью предлагаемых расчетных формул возможно решать некоторые задачи практического характера.
Например, требуется узнать минимальную нагрузку (P) на поверхность массива мерзлого грунта, предотвращающую его выпучивание. Массив образуется при зимнем промерзании (H) на глубину 1 м участка талого грунта размером 10х10 м и площадью S, соответственно, 100 м2; плотность талого грунта (ρт) 1.9 г/см3, плотность мерзлого грунта (ρм) 1.7 г/см3. По формуле (10) при hр = 0 (поскольку перемещение исключается) определяем величину нагрузки P без учета сопротивления сдвигу (Fс = 0) в 196 КН, (что соответствует минимальной массе возводимого на данном участке сооружения 20 т). Фактически же расчет сделан с некоторым запасом, так как не учитывалась Fс (т.е. масса сооружения может быть несколько меньше). Определим в тех же условиях высоту поднятия сооружений различной массы (например, 12 т и 7 т) вместе с мерзлым массивом. Согласно формуле (10) при Fс = 0 (сопротивление сдвигу не учитываем) при массе 12 т (P = 117,6 КН), сооружение поднимется на высоту, равную 0,04 м, а при массе 7 т (P = 68,6 КН) на 0,07 м.
Выводы
1. Криогенное пучение тонкодисперсных грунтов в условиях открытой системы может быть объяснено воздействием архимедовой силы, обусловленной разностью плотностей талого и мерзлого грунта.
2. Физическую сущность данного явлению раскрывает концепция выпучивания цельного мерзлого массива – литостатический механизм криогенного пучения.
3. Литостатический механизм подтверждается опытными лабораторными данными автора, а также результатами эксперимента В.О. Орлова.
4. Концепция литостатического механизма позволяет с помощью простых формул рассчитывать силовые эффекты, сопровождающие промерзание и пучение тонкодисперсных грунтов.
5. Дальнейшее развитие изложенных представлений могло бы быть перспективно как в научном, так и в практическом плане – в частности, при исследовании условий возникновения и развития форм криогенного пучения в природе, а также при изучении взаимодействия фундаментов с промерзающими грунтами их оснований.
Библиографическая ссылка
Марахтанов В.П. КРИОГЕННОЕ ПУЧЕНИЕ ТОНКОДИСПЕРСНЫХ ГРУНТОВ ПОД ВОЗДЕЙСТВИЕМ АРХИМЕДОВОЙ СИЛЫ // Международный журнал прикладных и фундаментальных исследований. – 2016. – № 4-4. – С. 748-759;URL: https://applied-research.ru/ru/article/view?id=9069 (дата обращения: 21.11.2024).