В инженерной и научной деятельности широко применяют моделирование и модели. Под моделированием понимают [1] построение действующей реальной модели или математической модели, обладающей свойствами, которые подобны свойствам или отношениям рассматриваемой естественной или технической системы. Таким образом, с помощью моделей имитируют работу систем и принимают предварительные решения относительно оптимизации ее характеристик.
Моделирование в инженерной практике определяется тем, что в большинстве практически значимых ситуациях невозможно изучить само явление или процессы, происходящие в создаваемом техническом объекте. Причинами возникновения таких ситуаций, например, могут быть большие размеры масштабы объекта изучения или недоступность его внутреннего пространства. Замена в таких ситуациях объекта моделью необходима, при этом важно уметь создать репрезентативную модель объекта.
В результате анализа моделей получают качественное представление об особенностях изучаемых процессов и устанавливают количественные закономерности, определяющие динамический ряд последовательных состояний, получают возможность предсказывать течение процесса во времени и определять его количественные характеристики.
Анализ научной литературы [1, 5, 6, 8, 10, 11, 12, 13] показал, несмотря на то, что моделирование используют давно, не существует общей методологии создания как реальных, так и всевозможных математических моделей. Созданию любой модели предшествует анализ репрезентативности модели, создание четкого представления, какие процессы в работе устройства модель отражает полно, какие частично, какие не отражает. Данный факт определил актуальность изучения и исследования данного вопроса.
Цель исследования – проанализировать виды моделирования, определить общую логику построения вероятностных моделей технических систем.
Цель исследования определила задачи исследования:
– выделить основные понятия методологии моделирования систем;
– определить особенности применения вероятностных моделей;
– определить место вероятностных моделей в общей логике построения моделей технических систем.
Одним из первых ученых, давший обобщенное определение модели был Г. Клаус. Согласно Г. Клауса, модель – это отображение фактов, вещей, отношений определенной области знаний в виде более простой и более наглядной материальной структуры [6]. Главное требование, предъявляемое к модели, выдвинутое Г. Клаусом – это «существенность сходства и несущественность различия с оригиналом» [6]. Клаус утверждал, что в моделировании сложных динамических систем можно достичь сходных результатов на основе сходства поведения, структуры и материала, из которого состоят системы.
А.И. Уемов рассматривает модель, как систему, исследование которой служит средством для получения информации о другой системе [13].
В.А. Штофф под моделью понимает мысленно представляемую или материально реализованную систему, которая отображает и воспроизводит объект так, что изучение модели дает новую информацию об объекте [11].
В энциклопедическом словаре «Информатика» под моделью объекта понимают «другой объект (реальный, знаковый или воображаемый), отличный от исходного, который обладает существенными для моделирования свойствами и в рамках этих целей полностью заменяет исходный объект» [4].
В Большой Российской энциклопедии [9] дается несколько вариантов термина «модель»:
1) модель – образец (эталон, стандарт) изделия для серийного производства, тип, марка изделия;
2) модель – образец изделия, служащий для изготовления формы при отливке и воспроизведении в другом материале;
3) модель – устройство, воспроизводящее, имитирующее строение и действие какого – либо другого (моделируемого) приспособления в научных, производственных или спортивных целях;
4) модель – схема, изображение или описание, какого – либо явления или процесса в природе и обществе.
Анализируя всевозможные определения модели, учитывая полноту определений и возможность применения определения модели при рассмотрении моделирования технических систем, было принято следующее определение модели: модель – это физический или абстрактный образ моделируемого объекта, удобный для проведения исследований и позволяющий адекватно отображать интересующие исследователя физические свойства и характеристики объекта.
Сделанный выбор, объясняется тем, что модель считают адекватной, если в модели отражаются исследуемые свойства с приемлемой точностью. Модели технических объектов, используемые при проектировании, предназначены для анализа процессов функционирования объектов и оценки их выходных параметров. Модели технических объектов должны отражать физические свойства объектов, существенные для решения конкретных задач.
Применительно к техническим системам моделирование – это процесс замещения объекта исследования некоторой его моделью и проведение исследований на модели с целью получения необходимой информации об объекте или системе [10].
Различают моделирование предметное и абстрактное.
Предметное моделирование – это построение физической модели, которая отображает основные физические свойства и характеристики моделируемого объекта. Физическое моделирование применялось при создании сложных технических объектов, с помощью изготовления макетного или опытного образца технического объекта. На макете проводились испытания, в результате которых определялись выходные параметры и характеристики, оценивалась надежность функционирования и степень выполнения технических требований, предъявляемых к объекту [10].
Физическое моделирование сложных технических систем сопряжено с большими временными и материальными затратами.
Абстрактное моделирование (математическое моделирование) – это построение абстрактной модели. Математическое моделирование дает возможность посредством математических символов, зависимостей составить описание функционирования технического объекта, определить выходные параметры и характеристики, получить оценку показателей эффективности и качества.
Процесс формирования математической модели, использование модели для анализа и синтеза называют математическим моделированием. Проведение исследований на модели называют экспериментом [8]. Поиск оптимального варианта для получения искомого результата связан с многократным проведением эксперимента в связи с многомерностью и многокритериальностью задачи. На заключительных этапах эксперимента используют вероятностные модели с целью исследования процессов функционирования технической системы в условиях максимально приближенным к реальным с использованием статистических методов обработки результатов.
Анализ научных работ, касающихся процесса моделирования [1, 6, 8, 10, 11, 12, 13] дал возможность определить общую логику построения моделей.
Процесс моделирования, как вид осознанной целенаправленной деятельности начинается с возникновения проблемы. Под проблемой следует понимать потребность изменить в лучшую сторону существующее состояние исследуемого объекта или системы.
Критерий качества создаваемой модели определяет цель исследования.
Содержательный анализ системы «задача – объект» и выбор способа формирования модели есть следующий шаг построения модели, основанный на априорных данных. Целесообразно использовать экспериментальное определение существенных для решаемой задачи свойств и характеристик объекта. Эксперимент осуществляют по разрабатываемому оптимальном плану. Данные эксперимента обрабатывают и берут за основу формализованного описания объекта в виде математической модели «вход – выход».
Формализованную модель оценивают по соответствующему, выбранному ранее критерию. Решение о принятии модели дает возможность проведения опытной проверки в условиях той задачи, для которой построена модель. Положительный результат опытной проверки приводит к проведению заключительного этапа – использование модели по прямому назначению для решения исследовательской задачи.
Таким образом, построение модели связано с введением ряда гипотез, часть из которых подтверждается, а часть отвергается. Наличие обратных связей, т.е. итеративный характер построения моделей, есть принципиальное свойство процесса моделирования.
Термин система применяют для характеристики исследуемого или проектируемого объекта.
Первоначально систему определяли, как элементы (части, компоненты) ai и связи (отношения) rj между ними [5]:
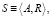 где
где 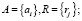
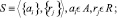
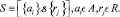
В первых двух записях система задана с помощью способов теоретико-множественных представлений: способы задания множеств, не учитывающие взаимоотношения между множествами элементов и связей. В третьей форме записи система записана не как простая совокупность элементов и связей того или иного вида, а только те элементы и связи, которые находятся в области пересечения 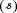 друг с другом.
друг с другом.
Берталанфи определял систему как комплекс взаимодействующих компонентов или как совокупность элементов, находящихся в определенных отношениях друг с другом и со средой [5].
В определении системы Месаровича [5] выделены множество X входных объектов, воздействующих на систему и множество Y выходных результатов. Между множествами X и Y установлено обобщающее отношение пересечения:
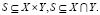
В определении Ф.Е. Темникова [5] система – организованное множество. В философском словаре система – совокупность элементов, находящихся в отношениях и связях между собой и образующих некоторое целостное единство [7]. В данных определениях системы появляется понятие цель.
Ю.И. Черняк определил систему как отображение на языке исследователя (конструктора) объектов, отношений и их свойств в решении задачи исследования [5].
Выше рассмотренные определения системы дают возможность принять утверждение, что объект-оригинал – естественная или искусственная, реальная или воображаемая система.
Система имеет множество параметров S0 и характеризуется определёнными свойствами. Количественной мерой свойств системы служит множество характеристик Y0, система проявляет свои свойства под влиянием внешних воздействий X. Множество параметров S и их значений отражает её внутреннее содержание – структуру и принципы функционирования. Характеристики S – это в основном её внешние признаки, которые важны при взаимодействии с другими S.
Характеристики S находятся в функциональной зависимости от её параметров. Каждая характеристика системы 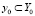 определяется ограниченным числом параметров
определяется ограниченным числом параметров 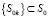 . Остальные параметры не влияют на значение данной характеристики S. Исследователя интересуют, как правило, только некоторые характеристики S:
. Остальные параметры не влияют на значение данной характеристики S. Исследователя интересуют, как правило, только некоторые характеристики S: 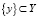 при конкретных воздействиях на систему
при конкретных воздействиях на систему 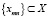 .
.
Модель – это система со своими множествами параметров Sm и характеристик Ym. Оригинал и модель сходны по одним параметрам и различны по другим. Замещение одного объекта другим правомерны, если интересующие исследователя характеристики оригинала и модели определяются однотипными подмножествами параметров и связаны одинаковыми зависимостями с этими параметрами:
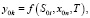
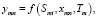
где, ymn – k-я характеристика модели, 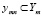 , xmn – внешнее воздействие на модель,
, xmn – внешнее воздействие на модель, 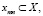 Tm – модельное время.
Tm – модельное время.
При этом
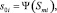
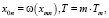
где m – масштабный коэффициент на всём интервале [0, Tm] или в отдельные периоды времени. Некоторым приближением делают вывод о том, что характеристики Op, связаны с характеристиками M зависимостями 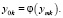 Множество характеристик модели
Множество характеристик модели 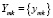 является отображением множества интересующих характеристик оригинала
является отображением множества интересующих характеристик оригинала
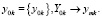
Классификацию моделей систем осуществляют по разным критериям в зависимости от целей и ресурсов системы.
Согласно теме исследования, были рассмотрены классификации систем согласно:
– отношению системы к окружающей среде;
– описанию переменных системы;
– описания закона функционирования системы;
– по способу управления системы.
По отношению к окружающей среде системы делят:
– открытые (присутствует обмен ресурсами с окружающей средой);
– закрытые (отсутствует обмен ресурсами с окружающей средой).
По описанию переменных, системы подразделяют:
– с качественными переменными (имеют содержательное описание);
– с количественными переменными (имеющие дискретные или непрерывно описываемые количественным образом переменные);
– смешанного описания (количественно – качественное).
По типу описания закона функционирования системы:
– «черный ящик», когда известны входные и выходные данные и неизвестен закон функционирования системы;
– не параметризованные, когда закон не описан, но известны некоторые априорные свойства закона;
– параметризованные, когда закон известен с точностью до параметров;
– «белый ящик», когда полностью известен закон.
По способу управления системой, системы делят:
– управляемые извне системы, без обратной связи, регулируемые, управляемые структурно, информационно или функционально;
– управляемые изнутри, самоуправляемые или регулируемые автоматически, адаптируемые с помощью управляемых изменений состояний, упорядочивающие свою структуру под воздействием внутренних и внешних факторов;
– с комбинированным управлением, т.е. автоматические, полуавтоматические, автоматизированные, организационные.
Вероятностные модели описывают ситуации, в которых похожие причины приводят к различным следствиям, т.е. имеет место элемент случайности. Для построения вероятностной модели необходимо знать, какие величины можно считать случайными, а какие – неслучайными, какой характер имеют законы распределения случайных величин.
Вероятностные модели разделяют на две большие группы [5]:
– теоретико-вероятностная – математическая модель, в которой можно точно указать законы распределения случайных величин;
– статистическая – математическая модель, в которой заранее нельзя указать законы распределения случайных величин.
По степени сложности вероятностные модели делят на три уровня сложности.
Простейшие теоретико-вероятностные модели первого уровня – это случайные события, являющиеся качественной характеристикой проведенного испытания и случайные величины, являющиеся количественной характеристикой проведенного испытания.
Случайное событие может быть элементарным или выраженным через элементарные. Для описания вероятностных свойств элементарного случайного события A используют стандартную формулу классической вероятности [3]:
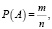
где m – число случаев из пространства элементарных событий, благоприятных событию A; n – общее число случаев, содержащееся в пространстве элементарных событий.
Для расчета вероятности используют теоремы сложения и умножения вероятностей [3]:
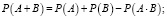
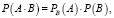
где PB(A) условная вероятность события A при условии, что событие B произошло.
Пусть 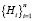 – полная несовместная группа событий (гипотез), тогда для определения вероятности сложных событий используется формула полной вероятности [3]:
– полная несовместная группа событий (гипотез), тогда для определения вероятности сложных событий используется формула полной вероятности [3]:
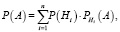
где P(Hi) – вероятность гипотезы Hi; 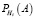 – условная вероятность события A при выполнении гипотезы Hi.
– условная вероятность события A при выполнении гипотезы Hi.
Случайные события и случайные величины связаны между собой через пространство элементарных событий. Вероятностные свойства дискретного типа описываются функцией дискретного аргумента
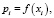
где xi – реализация случайной величины X; pi – соответствующая случайной величине вероятность; вероятностные свойства случайной величины непрерывного типа описывают функцией f(x) – плотность распределения, определенной на всей числовой оси, неотрицательной и нормированной на области определения [3].
В биномиальном законе распределения, реализуемом в схеме независимых испытаний, пространство элементарных событий дискретной случайной величины есть конечное множество целых чисел, включая 0, т.е.
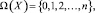
а вероятности значений рассчитывают по формуле Бернулли [3]:
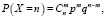
где 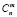 – число сочетаний из n по m; р – вероятность появления события в отдельном испытании,
– число сочетаний из n по m; р – вероятность появления события в отдельном испытании, 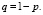
Нормальный закон распределения – один из основных для непрерывной случайной величины X задается плотностью распределения [3]:
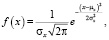
определенной для всех X и удовлетворяющей условиям f(x) > 0 и
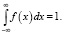
Математическое ожидание случайной величины 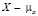 , среднее квадратическое отклонение – -x.
, среднее квадратическое отклонение – -x.
Универсальной формой закона распределения, имеющей место, как для дискретной, так и для непрерывной случайной величины, является функция распределения [3]
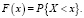
Второй уровень теоретико-вероятностной модели связан с системой случайных величин (многомерная случайная величина), вероятностные свойства которой не исчерпываются свойствами отдельных величин, образующих систему, а описываются также зависимостью между ними.
Для двумерной случайной величины (X, Y) рассматривают частные плотности распределения f1(x) и f2(x), а также совместную плотность f(x, y). Связь между частными плотностями распределения и совместной плотностью распределения устанавливают равенства:
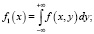
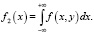
Совместная плотность распределения f(x, y) не всегда может быть определена через плотности f1(x) и f2(x). Для n –мерной случайной величины (X1, X2,…, Xn) функции распределения имеют более громоздкий вид, поэтому на модельном уровне при описании объекта используют набор числовых характеристик. Для двумерной случайной величины (X, Y) – это -x, -y, -x, -y, rxy; для n –мерной случайной величины – это 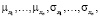 а также корреляционная матрица
а также корреляционная матрица 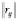 , где rij – коэффициент корреляции между случайными величинами Xi и Xj.
, где rij – коэффициент корреляции между случайными величинами Xi и Xj.
Обобщением модели n –мерной случайной величины служит модель третьего уровня – случайная функция X(t), где t – вещественный параметр [8].
Графически случайную функцию представляют в виде набора реализаций xi(t), где каждая xi(t) – неслучайная функция  (рис. 1) при фиксированном t = t0 получают сечение случайной функции X(t0), которая представляет собой одномерную случайную величину.
(рис. 1) при фиксированном t = t0 получают сечение случайной функции X(t0), которая представляет собой одномерную случайную величину.
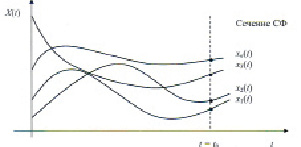
Рис. 1. Случайная функция X(t) в виде набора реализации xi(t)
Полное вероятностное описание случайной функции связано с заданием бесконечномерного закона распределения всех сечений случайной функции X(t).
На модельном уровне ограничиваются рассмотрением случайной функции в рамках корреляционной теории, т.е. рассматривают математической ожидание случайной функции -x(t) и корреляционной функции Kx(t1, t2), которые являются неслучайными функциями соответственно одного или двух аргументов [8].
Каждому из уровней теоретико-вероятностных моделей соответствует своя статистическая модель.
В основу построения статистической модели положены некоторые допущения. В зависимости от математической сути различают три основные модели математической статистики [2]:
1) модель выборки;
2) модель регрессии;
3) модель случайного процесса.
Каждая из статистических моделей связана с исходным материалом и решет свои задачи, но все модели математической статистики имеют дело с большим объемом информации и трудоемкими методами обработки этой информации. Реализация статистических моделей осуществляется на компьютере.
В тех случаях, когда получение исходных статистических данных путем организованных экспериментов невозможно, статистический материал получают с помощью специально созданных математических моделей, основу которых составляет статистическое моделирование на компьютере случайных событий и случайных величин. Такой метод моделирования называют методом статистических испытаний или методом Монте-Карло.
Простейшей статистической моделью считают одномерную модель выборки [2], в которой предполагается, что исходный статистический материал есть реализация одной случайной величины X с законом распределения F(x).
Основой для построения одномерной модели выборки служит простая случайная выборка, представленная в виде ряда наблюдений (табл. 1).
Таблица 1
Случайная выборка
|
i |
1 |
2 |
… |
n |
|
xi |
x1 |
x2 |
… |
xn |
Примером может служить измерение расстояния до цели каким-либо прибором. Результат измеряется от опыта к опыту, так как имеет место воздействие случайных причин.
Реализация модели связана с построением эмпирических законов распределения: f*(x) – статистическая плотность распределения; F*(x) – статистическая функция распределения, аналогичная теоретическим законам для случайной величины X. Графическое представление функции f*(x) есть гистограмма, а графическим представлением функции F*(x) есть кривая накопленных частот.
Очевидно, что найденные законы содержат элемент случайности, так как законы определены по конечному числу наблюдений. Для уточнения модели проводят сглаживание статистического ряда, для чего используют, например, критерии согласия Пирсона, Колмогорова.
В некоторых ситуациях ограничиваются получением точечных и интервальных оценок основных числовых характеристик -x и 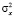 .
.
Если результаты наблюдений зависят от некоторого параметра и изменяются от измерения к измерению не только за счет случайных причин, но и за счет существенных, то модель выборки неприменима к данному ряду наблюдений. В этом случае используют модель регрессии, которая предполагает, что статистический материал представляет собой реализации случайной величины, изменяющейся в зависимости от какого-либо параметра, например от времени или от пространственной координаты.
Исходный ряд наблюдений имеет вид, приведенный в табл. 2, где tn – значение параметра (i = 1, 2, …, n); xn – значение случайной величины, соответствующее значению параметра.
Таблица 2
Исходный ряд наблюдений
|
ti |
t1 |
t2 |
… |
tn |
|
xi |
x1 |
x2 |
… |
xn |
Основным предположением модели регрессии, которое сводит модель к модели выборки, принимают, что реализации случайной величины могут быть представлены в виде суммы
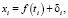
где f(ti) – неслучайная функция аргумента t; -i – ошибки, содержащиеся в выборке. Предполагается, что ряд наблюдений {x1, x2,…, xn} есть реализация системы независимых случайных величин (X1, X2,…, Xn), частные распределения которых одинаковы, за исключением математического ожидания, для которого.
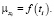
Функцию f(t) называют сглаживающей, а график функции f(t) называют линией регрессии.
Основная задача модели регрессии – это определение линии регрессии f(t) и оценка точности результата (рис. 2).
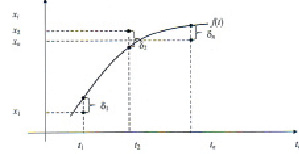
Рис. 2 Линия регрессии f(t) и оценка точности результата -
Сглаживающую функцию задают параметрически f(a1, a2,…, am, t), где вид функции известен и вычисляют только параметры
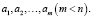
Для определения параметров используют метод наименьших квадратов, основанный на соотношении
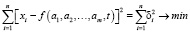
сумма квадратов отклонений результатов наблюдений от сглаживающей кривой должна быть наименьшей.
В большинстве прикладных задач ограничиваются линейной регрессией.
Модель случайного процесса есть обобщение модели выборки и модели регрессии. Исходный ряд наблюдений зависит от параметра, как в модели регрессии, а случайные величины (X1, X2,…, Xn), реализацией которых является данный ряд, зависимы и также зависимы случайные ошибки -i в случайных измерениях.
Основное предположение модели случайного процесса в том, что ряд наблюдений, зависящих от параметра, есть значения функции x(t), являющейся реализацией случайной функции X(t), распределение и характеристики которой заранее неизвестны.
Пусть имеется m рядов наблюдений, проведенных в одних и тех же условиях. Данные сводят в таблицу, в которой в строках расположены реализации, а в столбцах – сечения по параметру t (табл. 3).
Таблица 3
Ряды наблюдений, проведенных в одних условиях
|
x(t) |
t |
|||
|
t1 |
t2 |
… |
tn |
|
|
x1(t) |
x1(t1) |
x1(t2) |
… |
x1(tn) |
|
x2(t) |
x2(t1) |
x2(t2) |
… |
x2(tn) |
|
… |
… |
… |
… |
|
|
xm(t) |
xm(t1) |
xm(t2) |
… |
xm(tn) |
Обработка данных таблицы может вестись как по столбцам (модель выборки), так и по строкам (модель регрессии). Полученные при различных значениях аргумента t результаты числовых характеристик аппроксимируют по методу наименьших квадратов аналитическими выражениями.
При статистическом моделировании применяют метод статистических испытаний – метод Монте-Карло. Результаты, полученные при воспроизведении на имитационной модели процесса функционирования системы, есть реализации случайных величин и функций. Для нахождения характеристик процесса требуется многократное воспроизведение с последующее статистической обработкой информации.
Основная идея метода Монте-Карло заключается в следующем.
Пусть необходимо определить значение детерминированной величины y, которую можно представить в виде детерминированной функции
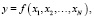
где xi – детерминированная переменная.
Переменные x1, x2,…, xN заменяют на случайные функции с известным законом распределения. Значение y заменяют на случайную величину Y. Данную задачу решают по следующему алгоритму:
1) по каждой из величин x1, x2,…, xN производят случайное испытание, в результате которого определяют некоторое конкретное значение случайной величины x1i, x2i,…, xNi;
2) используя найденные величины, определяют одно частное значение yi по выше приведенной зависимости;
3) предыдущие операции повторяются N раз, в результате чего определяют N значений случайной величины Y;
4) на основании N значений случайной величины Y находят эмпирическую функцию случайной величины Y, математическое ожидание -y и дисперсию 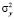 .
.
Обработка результатов моделирования сводится к оценке некоторых моментов. При независимых наблюдениях значений случайной величины Y в качестве таких оценок используют:
– выборочное среднее
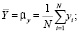
– выборочную дисперсию
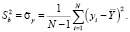
Величины 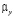 и
и 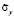 используют в качестве оценок математического ожидания -y и дисперсии
используют в качестве оценок математического ожидания -y и дисперсии 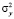 .
.
Заключение
Согласно поставленным задачам исследования были выделены основные понятия методологии моделирования, применимые к моделированию технических систем:
1) модель – это физический или абстрактный образ моделируемого объекта, удобный для проведения исследований и позволяющий адекватно отображать интересующие исследователя физические свойства и характеристики объекта;
2) моделирование – это процесс замещения объекта исследования некоторой его моделью и проведение исследований на модели с целью получения необходимой информации об объекте или системе;
3) в основе современной методологии моделирования положен системный подход, и технический объект рассматривают как сложную систему, состоящую из взаимосвязанных, целенаправленно функционирующих элементов и взаимодействующую с окружающей средой;
4) построение модели связано с введением ряда гипотез, часть из которых подтверждается, а часть отвергается; наличие обратных связей, т.е. итеративный характер построения моделей, есть принципиальное свойство процесса моделирования;
5) модель – это система со своими множествами параметров Sm и характеристик Ym; оригинал и модель сходны по одним параметрам и различны по другим; замещение одного объекта другим правомерны, если интересующие исследователя характеристики оригинала и модели определяются однотипными подмножествами параметров и связаны одинаковыми зависимостями с этими параметрами.
В работе определены особенности применения вероятностных моделей:
– для построения вероятностной модели необходимо знать, какие величины можно считать случайными, а какие – неслучайными, какой характер имеют законы распределения случайных величин.
Работа с научной литературой и анализ рассматриваемых в ней вопросов дал возможность определить место вероятностных моделей в общей логике построения моделей технических систем.
1. Простейшие теоретико-вероятностные модели первого уровня – это случайные события, являющиеся качественной характеристикой проведенного испытания и случайные величины, являющиеся количественной характеристикой проведенного испытания.
2. Второй уровень теоретико-вероятностной модели связан с системой случайных величин (многомерная случайная величина), вероятностные свойства которой не исчерпываются свойствами отдельных величин, образующих систему, а описываются также зависимостью между ними.
На модельном уровне ограничиваются рассмотрением случайной функции в рамках корреляционной теории, т.е. рассматривают математической ожидание случайной функции -x(t) и корреляционной функции Kx(t1, t2), которые являются неслучайными функциями соответственно одного или двух аргументов.
3. Каждому из уровней теоретико-вероятностных моделей соответствует своя статистическая модель.
В тех случаях, когда получение исходных статистических данных путем организованных экспериментов невозможно, статистический материал получают с помощью специально созданных математических моделей, основу которых составляет статистическое моделирование на компьютере случайных событий и случайных величин. Такой метод моделирования называют методом статистических испытаний или методом Монте-Карло. Простейшей статистической моделью считают одномерную модель выборки.
Если результаты наблюдений зависят от некоторого параметра и изменяются от измерения к измерению не только за счет случайных причин, но и за счет существенных, то в этом случае используют модель регрессии, которая предполагает, что статистический материал представляет собой реализации случайной величины, изменяющейся в зависимости от какого-либо параметра, например от времени или от пространственной координаты.
Модель случайного процесса есть обобщение модели выборки и модели регрессии. Исходный ряд наблюдений зависит от параметра, как в модели регрессии, а случайные величины (X1, X2,…, Xn), реализацией которых является данный ряд, зависимы и также зависимы случайные ошибки -i в случайных измерениях.
Библиографическая ссылка
Бунтова Е.В. МОДЕЛИРОВАНИЕ ТЕХНИЧЕСКИХ СИСТЕМ // Международный журнал прикладных и фундаментальных исследований. 2016. № 5-5. С. 709-717;URL: https://applied-research.ru/ru/article/view?id=9503 (дата обращения: 17.11.2025).

