Одним из эффективных способов вычисления преобразования Фурье является сведение к вычислению свертки. В настоящее время наибольшее применение нашли два различных способа перехода от преобразования Фурье к свертке – алгоритм Блюстейна и алгоритм Рейдера для простых чисел [1, с. 60-97, 2].
Алгоритм Блюстейна описывается равенством
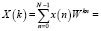
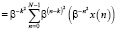 , (1)
, (1)
где – квадратный корень из 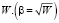 .
.
Данный алгоритм содержит n поточечных умножений x(n) на 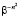 , циклическую свертку с
, циклическую свертку с 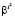 в КИХ фильтре с n отводами и следующие за этим n поточечных умножений на
в КИХ фильтре с n отводами и следующие за этим n поточечных умножений на 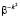 . Поэтому полное число операций имеет порядок n2. Однако в некоторых приложениях он допускает более простую аппаратную реализацию, кроме того, прямое вычисление свертки можно заменить алгоритмами быстрой свертки [1, С. 57-59, 3, С. 76, 5, с. 77].
. Поэтому полное число операций имеет порядок n2. Однако в некоторых приложениях он допускает более простую аппаратную реализацию, кроме того, прямое вычисление свертки можно заменить алгоритмами быстрой свертки [1, С. 57-59, 3, С. 76, 5, с. 77].
С этой точки зрения предпочтительным является алгоритм Рейдера. Он содержит совокупность операций по переиндексации входных данных и циклическую свертку, длина которой равна N – 1.
Алгоритм Рейдера может применяться для вычисления преобразования Фурье в любом поле Галуа, если длина преобразования N является простым числом. Для реализации алгоритма Рейдера выбирается примитивный элемент простого поля Галуа GF(N). Тогда каждый элемент этого поля – целое число меньше N, можно записать в виде степени элемента . В этом случае дискретное преобразование Фурье можно переписать, заменив индексы n и k соответствующими степенями элемента . При значениях n = 0 и k = 0 полученные компоненты ДПФ выводятся отдельно, т.е.
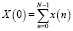 (2)
(2)
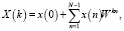
где k = 1, 2, …, N – 1.
Для сведения вычисления ДПФ к свертке определяют отображение множества элементов n {1, 2, …, N – 1} поля на соответствующее множество {1, 2, …, N – 1} чисел r(n), где r(n) = n. Таким образом обеспечивается перестановка в матрице поворачивающих коэффициентов ДПФ. Тогда дискретное преобразование Фурье можно записать в виде
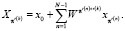 (3)
(3)
Так как r(n) задает перестановку, то можно получить l = r(k) и j = N – 1 – r(n). Это позволяет получить свертку
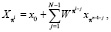 (4)
(4)
где 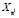 и
и 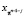 – соответственно переставленные компоненты последовательностей входных и выходных данных. Таким образом, перестановка индексов входных и выходных данных позволяет записать ДПФ в виде свертки. Основным достоинством алгоритма Рейдера является простота его сведения к алгоритму Винограда для свертки, характеризующейся минимальным числом умножений.
– соответственно переставленные компоненты последовательностей входных и выходных данных. Таким образом, перестановка индексов входных и выходных данных позволяет записать ДПФ в виде свертки. Основным достоинством алгоритма Рейдера является простота его сведения к алгоритму Винограда для свертки, характеризующейся минимальным числом умножений.
Однако, несмотря на хорошие показатели в области обеспечения высокой скорости обработки сигналов, БПФ характеризуется и рядом недостатков. Во-первых, это значительные схемные затраты, связанные с необходимостью параллельной реализацией базовой операции БПФ «бабочка». Во-вторых, входные данные, а также промежуточные и выходные результаты являются комплексными числами. Следовательно, вычислительное устройство должно два вычислительных тракта, для обработки действительной и мнимой частей. Даже если входные данные действительны, то это требование сохраняется, так как промежуточные результаты могут быть комплексными числами.
В-третьих, в процессе вычислений спектра от этапа к этапу модули чисел увеличиваются, поэтому их нужно масштабировать сдвигом вправо. Действительно, сели последовательность {x(n)} из N отсчетов имеет спектральные коэффициенты {X(k)}, то согласно теореме Парсеваля
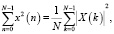 (5)
(5)
т.е. средняя мощность выходных гармоник в N раз превышает среднюю мощность исходной последовательности. Отсюда следует необходимость масштабирования результатов из-за опасности переполнения разрядной сетки [4, С. 53-54].
В-четвертых, реализация ортогональных преобразований на основе использования математической модели ЦОС поля комплексных чисел характеризуется значительными погрешностями [5, с. 77, 10, С. 22-25].
В настоящее время при исследовании работы вычислительных устройств, используемых для ЦОС, выделяют следующие три источника погрешностей, возникающих вследствие конечной длины обрабатываемых операндов [12, с. 188-193, 14, с. 391-400]:
– квантование входного сигнала;
– квантование коэффициентов;
– округление результатов арифметических операций.
Квантование входного сигнала осуществляется аналого-цифровым преобразователем (АЦП). Входной непрерывный сигнал x(t) периодически дискретизируется, и каждая выборка кодируется в виде двоичного кода длиной B разрядов. Прежде чем выборка x(n) кодируется, она видоизменяется так, чтобы принять только одно из 2B возможных значений. При этом погрешность квантования определяется
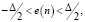 (6)
(6)
где – величина шага квантования, определяемая аналого-цифровым преобразователем.
Таким образом, погрешность квантования входного сигнала ограничивается половиной шага квантования.
При практической реализации вычислительного устройства ЦОС поворачивающие коэффициенты всегда квантуются [11, с. 367-371]. Положим, что для представления коэффициентов используются BI бит. Тогда реальные поворачивающие коэффициенты представляются
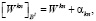 (7)
(7)
где kn – погрешность вследствие квантования поворачивающих коэффициентов, удовлетворяющее условию
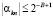 (8)
(8)
Известно, что для представления знака поворачивающего коэффициента Wkn и его целой части достаточно по одному биту. Тогда последний бит представляет значение 2–B + 2.
В результате спектральные составляющие входной последовательности x(n) будут определяться
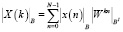 (9)
(9)
При этом при увеличении частоты дискретизации влияние погрешностей квантования поворачивающих коэффициентов увеличивается [6, С. 76-78].
Вопросам определения погрешности округления результатов арифметических операций в настоящее время уделяется значительное внимание [8, с. 23-24].
Анализ выражения (1) показывает, что в состав спецпроцессора ДПФ должен входить умножитель для вычисления частных произведений
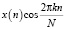 и
и 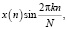
k = n = 0, 1, …, N – 1,
а также два накапливающих сумматора, для вычисления действительной и мнимой части спектральных составляющих.
Если положить, что входные выборки x(n) изменяются в пределах ± 1, а квантование и кодирование осуществляются двоичным кодом длиной B бит, включая знаковый разряд, то величина 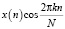 , являющаяся произведением B – битового операнда на BI – битовое слово, имеет размерность B + BI бит. Для того чтобы поместить ее в B – битовый регистр данных, произведение должно быть укорочено. Известны два способа выполнения данной процедуры [12, с. 188-193]:
, являющаяся произведением B – битового операнда на BI – битовое слово, имеет размерность B + BI бит. Для того чтобы поместить ее в B – битовый регистр данных, произведение должно быть укорочено. Известны два способа выполнения данной процедуры [12, с. 188-193]:
– усечение;
– округление.
При усечении сохраняются старшие B бит, а при округлении вначале к B – битому разряду прибавляется 1, если (B + 1)-й бит равен 1, а затем результат усекается до B бит.
Очевидно, что округление является более точным, но оно требует дополнительных временных и схемных затрат.
Рассмотрим случай округления выражения (1.1) следует отметить, что процесс округления (B + BI) – битового произведения до B бит подобен квантованию. Действительно, округление приводит к погрешности ограниченной величиной 2–B по абсолютному значению. Согласно [Арутюнов] такая погрешность округления может рассматриваться как шум с нулевым средним и дисперсией
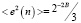 (10)
(10)
При вычислении спектральных составляющих согласно (1) формируется порядка N2 произведений, и каждая из них вносит такую погрешность квантования. Необходимо отметить, что если 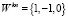 , то при вычислениях с этим коэффициентом погрешность не вносится. Кроме того, если при сложении парных произведений не происходит переполнение B – битового регистра данных, то погрешность не вносится. Этого можно достигнуть путем правильного масштабирования входного сигнала {x(n)}, как показано в работе [6, С. 76-78]. При соблюдении этих условий суммарная погрешность, вносимая при вычислении спектральных составляющих X(k), определяется (N2 – N) погрешностью квантования вследствие операции умножения.
, то при вычислениях с этим коэффициентом погрешность не вносится. Кроме того, если при сложении парных произведений не происходит переполнение B – битового регистра данных, то погрешность не вносится. Этого можно достигнуть путем правильного масштабирования входного сигнала {x(n)}, как показано в работе [6, С. 76-78]. При соблюдении этих условий суммарная погрешность, вносимая при вычислении спектральных составляющих X(k), определяется (N2 – N) погрешностью квантования вследствие операции умножения.
Так как погрешности независимы и представляют собой белый шум, то погрешность окружения на входе СП ДПФ имеет нулевое среднее и дисперсию, равную
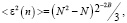 (11)
(11)
где 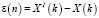 – разность между реальным XI(k) и идеальным X(k) выходным сигналом СП.
– разность между реальным XI(k) и идеальным X(k) выходным сигналом СП.
Таким образом, проведенные исследования показали, что из отмеченных трех источников погрешностей определяемых математической моделью ЦОС, погрешность округления результатов арифметических операций является наиболее серьезной. Следовательно, применение математической модели ЦОС, позволяющей свести к минимуму данную погрешность, является актуальной.
Данная задача предопределила интерес разработчиков СП ЦОС к математическим моделям цифровой обработки сигналов, обладающих свойством кольца и поля [7, С. 71-73].
Библиографическая ссылка
Тимошенко Л.И. ПРИМЕНЕНИЕ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ В ЦИФРОВОЙ ОБРАБОТКЕ СИГНАЛОВ // Международный журнал прикладных и фундаментальных исследований. 2016. № 5-5. С. 722-725;URL: https://applied-research.ru/ru/article/view?id=9505 (дата обращения: 28.12.2025).

