К задачам уравнения колебаний приводят многие вопросы математической физики, представляющие теоретической интерес и имеющие большое прикладное значение.
Решён широкий круг задач для круговых и прямоугольных областей. Для областей, не являющихся таковыми применяются различные методы, в частности приводящие к интегральным уравнениям. Однако, последние служат для доказательства существования и единственности решения. В основном эти задачи решаются численными методами. Немалый интерес представляют простые решения задач для областей частного вида.
Ниже рассматривается движение мембраны это различных случаев закрепления.
Поперечные колебания тонкой плоской мембраны, которой сообщено равномерное напряжение, можно рассматривать аналогично колебаниям струны с тем лишь дополнением, что число независимых переменных, входящих в дифференциальное уравнение, будет теперь равно трём вместе двух [1, 2].
Уравнение движения мембраны имеет вид:
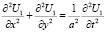
где U перемещение
В случае колебательного движения, т.е.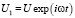 
оно примет вид
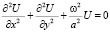(1)
Аналогичные уравнения могут быть получены для потенциалов перемещений при плоском движением упругого тела.
Рассмотрим следующей класс частных решений уравнения (1)
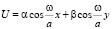(2)
В случае α = β, приравняв U из (2) нулю, т.е.
,
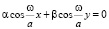получим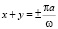 
, что отвечает закреплению мембран на квадратном контуре (рис. 1). Полагая
,
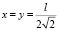получим
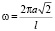(3)
выражение частоты для квадрата со стороной l, что известно из литературы.
Теперь рассмотрим случай α ≠ β. Приравняв U из (2) нулю, получим
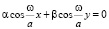(4)
Что соответствуют закреплению мембран на участках ABC (рис. 2)
Пологая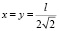 
, получим (3), т.е. частота не зависит от α и β (от угла поворота сторон ABC многоугольника). В частности, при α = 0 имеем прямоугольную мембрану, закрепленную с двух противоположных сторон.
Сравним частоту колебаний квадрата (3) с частотами выписанной и описанной окружностей, которые определяются из уравнения
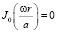(5)
где J0 – функции Бесселя нулевого порядка.
Из (5) для первой частоты
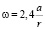(6)
Мембраны некруговой формы могут использоваться в ограждениях, для перекрытия оконных проемов, в качестве парусов на судах и.т.
Здесь рассматриваются свободные колебания мембран, закрепленных с двух сторон при различных закреплениях; аналогичные задачи могут быть рассмотрены и для пластин.
Изменяя отношения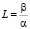 
можно менять форму мембраны при 
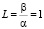имеет место квадратная мембрана; при L = 0 имеет место прямоугольная мембрана с двух сторон закрепленная, а с двух других свободная.
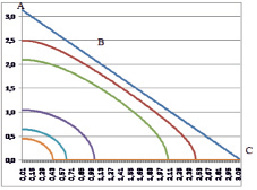
Рис. 1. K = 0; K = 0.2; K = 0.5; K = 1.5; K = 1.8; K = 1.9; L = 1
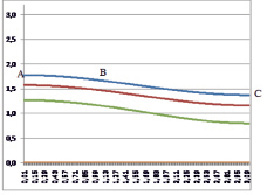
Рис. 2. K = 0; K = 0.2; K = 0.5; K = 1.5; K = 1.8; K = 1.9; L = 0.2
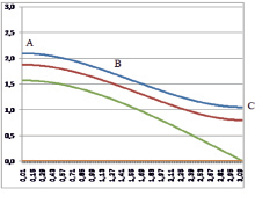
Рис. 3. K = 0; K = 0.2; K = 0.5; K = 1.5; K = 1.8; K = 1.9; L = 0.5
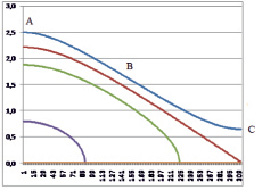
Рис. 4. K = 0; K = 0.2; K = 0.5; K = 1.5; K = 1.8; K = 1.9; L = 0.8
На рисунках показаны четыре варианта (L = β/α) мембран, закрепленных с двух сторон по криволинейным за исключением первой, границам. Две другие границы, прямолинейные свободны. Также на рисунках показаны линии уровня мембран для U = K. На рис. 1 представлена квадратная мембрана, решение для которой известно.
Рис. 1. соответствует L = 1, т с квадратной мембране, рис. 2 L = 0,2, рис. 3 L = 0,5, рис. 4 L = 0,8.
Библиографическая ссылка
Агаларов Дж.Г., Мамедова Г.А., Агасиев С.Р. КОЛЕБАНИЯ НЕКРУГОВЫХ МЕМБРАН // Международный журнал прикладных и фундаментальных исследований. – 2016. – № 6-2. – С. 199-201;URL: https://applied-research.ru/ru/article/view?id=9580 (дата обращения: 23.11.2024).