Простые числа Мерсенна относятся к специальным числам и играют важную роль в Теории чисел и имеют прикладное значение. В частности, на основе простых чисел Мерсенна создается генератор случайных чисел, являющихся базовыми элементами криптографии.
Числа вида
2n – 1, (1.1)
где n – 1, 2, 3…, называются числами Мерсенна. Марен Мерсенн (1588–1648 гг.) – французский математик, физик, философ и богослов, теоретик музыки.
Если число 2n – 1 – простое, то это число называется простое число Мерсенна, а число n – простое число и записывается оно так:
2p – 1, (1.2)
где p – простое число [9, 234].
В настоящее время известно 48 простых чисел Мерсенна. Это числа с показателями p: 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, … , и последнее 48-е число с показателем p = 55885161. Простые числа Мерсенна записывается так:
M2 = 3, M3 = 7, …, M13 = 8191, … (1.3)
Первые 7 простых чисел были вычислены Мерсенном, простота числа M31 была доказана Л. Эйлером, а число M61 было вычислено русским математиком-самоучкой, священником И.М. Первушиным. Простые числа Мерсенна начиная с показателя p = 521 были вычислены электронными вычислительными машинами и суперсовременными компьютерами [9, 234–235; 11, 77–79].
Число простых чисел бесконечно. Первым это утверждение доказал древнегреческий математик в 3-м веке до н.э. Евклид, затем были доказательства Л. Эйлера и других математиков. Хотя простые числа Мерсенна удерживают лидерство среди всех известных простых чисел по размерности вопрос бесконечности простых чисел Мерсенна остается открытым. [4, 7–8; 5, 9–10; 6, 11–12; 7, 28–31].
Критерии простоты чисел Мерсенна
Необходимым условием простоты чисел 2n – 1 является простота числа n, ведь если число n – составное, то и число 2n – 1 – составное. Но это условие не является достаточным. На самом деле, числа M11, M23, M29 и многие другие числа Мерсенна с простыми показателями являются составными. В 1878 году французский математик Э. Люка нашел метод определения простоты чисел Мерсенна, а позже, в 1932 году американский математик Д.Х. Лемер упростил этот метод и поэтому он носит название Метода Люка-Лемера:
Число Mp = 2p – 1, где p – простое число, является простым тогда и только тогда, когда (p – 1)-й член реккурентной последовательности
c1 = 4, c2 = 42 – 2 = 14, c3 = 142 – 2 = = 194, … , ck = ck – 12 – 2 (2.1)
делится на Mp, т. е. когда
cp – 1 ≡ 0(mod Mp) [9, 234–235; 11,78–79]. (2.2)
Этот метод является очень трудоемким, т.к. число Mp и число cp – 1 при больших значениях p вырастают до гигантских численных значений и вследствие этого выполнение всех математических действий становится сложным. Например, для вычисления последнего найденного 48-го простого числа Мерсенна потребовались мощности 360-ти процессорных ядер в течении 39 суток, т.е. чуть менее одной тысячи непрерывных машинных часов. [http://www.46tv.ru/line/world/013649/, Great Internet Mersenne Prime Search].
Существуют также критерии проверки чисел Мерсенна на делимость.
Критерий делимости числа Мерсенна, установленный Л. Эйлером: если p = 4n + 3 и q = 2p + 1 = 8n + 7 оба простые, то
Mp ≡ 0 (mod q) [9, 235] (2.3)
Критерий делимости чисел Мерсенна вида p = 4n + 1 не установлен, вследствие невозможности определения формулы числа q, и потому числа Мерсенна требуют общего критерия делимости и для чисел вида p = 4n + 1 и для чисел вида p = 4n + 3. В случае нахождения такого критерия появится возможность определения простоты числа Мерсенна, кроме метода Люка-Лемера. Но возможно ли такое?
Нахождение делителя числа Мерсенна
Л. Эйлер указал на обязательное условие делителя числа Мерсенна: это простое число имеет вид 2pk + 1, где p – показатель степени, k = 1, 2, 3, … , [9, 234–235].
На основании теоремы Ферма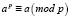 
т.е. 
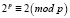, имеем 
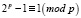, [1, 44–46; 3, 757–761; 8, 47–48; 10, 90–91]. Поэтому второй сомножитель этого числа будет иметь также вид 2pk2 + 1, где – k2 = 1, 2, 3, …, причем k ≠k2, иначе число 2p – 1 будет квадратом некоторого натурального числа, что невозможно изначально.
Итак, мы установили, что если число Мерсенна составное, то оно представимо в виде:
2p – 1 = (2pk1 + 1)(2pk2 + 1). (3.1)
Примем, что k1 < k2, и, соответственно будет 2pk1 + 1 < 2pk2 + 1, а вследствие этого
2pk1 + 1 <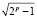 
, 2pk2 + 1 > 
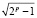. (3.2)
Равенство (3.1) преобразуем:
2p – 1 = (2pk1 + 1)(2pk2 + 1) = = 4p2k1k2 + 2pk1 + 2pk2 + 1, (3.3)
далее,
2p – 2 = 2p(2pk1 + k1 + k2), (3.4)
или
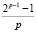= 2pk1k2 + k1 + k2, (3.5)
или
2pk1k2 + k1 + k2 –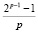 
= 0. (3.6)
Мы получили Диафантово уравнение 1-ой степени вида:
ax + by +cz +d = 0, (3.7)
где
a = 2p, x = k1k2, b = 1, y = k1, c = 1,
z = k2, d = –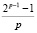 
.
До настоящего времени это уравнение считается неразрешимым. В случае решения этого вида Диофантового уравнения будет решен вопрос определения простоты чисел Мерсенна. Эти задачи разрешимы в случае решения вопроса матричных операторов, составленных из коэффициентов вышеуказанного уравнения. Но таковых пока нет [2, 265–279; 10, 4–5].
Вернемся к первому неравенству в выражении (3.2) и преобразуем его:
2pk1 + 1 <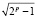 
,
т.е.
1 ≤ k1 <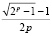 
, (3.8)
и, пренебрегая единицами в последней формуле, получаем:
1 ≤ k1 <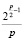 
. (3.9)
Теперь подставляя значения k1 от единицы до максимального значения в формулу 2pk1 + 1 и проводя операции до результата
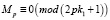(3.10)
получим первый наименьший простой делитель числа Мерсенна.
В противном случае, т.е. если при всех возможных значениях k1 по формуле (3.9) получим
Mp ≢ 0(mod(2pk1 + 1)), (3.11)
то число Mp – простое.
Заключение
Практическое применение нашего способа лучше метода Люка-Лемера в том, что при расчетах нет необходимости вычислять число Мерсенна, ведь оно содержит огромное число цифр. В нашем методе необходимо вести расчет до величины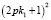 
, которое несопостовимо меньше самого числа Мерсенна.
При программном обеспечении расчет целезообразнее вести по формуле:
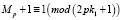, (4.1)
т.е.
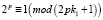, (4.2)
так как число 2p можно разделить по частям для облегчения расчетов. При программном обеспечении можно минимизировать число математических действий на основании свойств чисел Мерсенна и его делителей, что намного разгрузит компьютеры по сравнению с вычислениями по методу Люка-Лемера.
Библиографическая ссылка
Ибрагимов Р., Уштенов Е.Р. ОБ ОДНОМ КРИТЕРИИ ДЕЛИМОСТИ ЧИСЕЛ МЕРСЕННА // Международный журнал прикладных и фундаментальных исследований. – 2016. – № 7-5. – С. 786-788;URL: https://applied-research.ru/ru/article/view?id=9960 (дата обращения: 19.04.2024).