Несущей основой тонкостенных оболочек тетрагональной структуры является пространственная симметричная система стержней, соединенных между собой, а также с опорными силовыми элементами в равностоящих точках. Так, каркас цилиндрической оболочки тетраструктуры образуется двумя семействами ребер-стержней постоянного сечения, концы которых скреплены с краевыми шпангоутами таким образом, что точки их соединения между собой и шпангоутом делят его окружность на равные дуги.
При этом семейству ребер, направленных под некоторым углом +φ к образующей оболочке, соответствует семейство ребер, направленных к ней под углом -φ. Дополнительно эти стержни скреплены в равностоящих точках их взаимного пересечения по длине.
В общем случае эти ребра цилиндрического каркаса представляют собой стержни со спиральной осью. Вместе с тем, широкое применение получили конструкции такого типа, оси которых прямолинейны. При малых значениях углов φ можно приближенно считать, что они лежат на поверхности, близкой к цилиндрической.
Особенности геометрии
Расчет колебаний таких систем в предположении линейности их характеристик целесообразно проводить методом функции динамической податливости, понимая под этим термином амплитудное значение перемещений любой произвольно определенной точки А системы под действием единичной гармонической нагрузки, приложенной к ней в произвольной точке В [1].
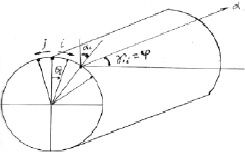
Колебания элементов системы будем рассматривать в следующих координатных осях. Исходное положение точки оси любого стержня с номером і определяется центральным углом θі, который отсчитывают от начального радиуса опорного шпангоута, и координатой S по оси стержня. Перемещения точки x будем определять в направлении его продольной оси 1і и главных центральных осей 2і и 3і, которые в общем случае могут быть повернуты на некоторый угол αі между осями 3і, радиусом каркаса и углом γі между продольной осью стержня и линией, паралельной оси каркаса. Так, для каркаса, образованного спиральными элементами αі = 0 γіi = ± φ. Для каркаса, собранного из прямых стержней без закрутки относительно продольной оси
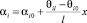 . (1)
. (1)
Угол γі = γ можно определить из соотношения
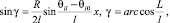 (2)
(2)
где θi0 – центральный угол, отсчитываемый от начального радиуса нулевого шпангоута до точки его соединения стержнем; θil – центральная угловая координата і-го стержня на втором (конечном)опорном шпангоуте; R – радиус опорных шпангоутов; l – длина стержней; L – расстояние между опорными шпангоутами.
При малой разности θl – θ0 можно полагать приближенно, что
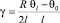 .
.
Определим кривизну спирального стержня в виде
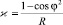 . (3)
. (3)
Степень закручивания стержней:
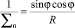 . (4)
. (4)
При малых φ можно приближенно считать, что
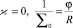 . (5)
. (5)
Угол закручивания сечения с координатой x определяется,
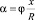 (6)
(6)
или
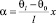 . (7)
. (7)
Пусть каркас состоит из N стержней, направленных к его оси углом φ, и N стержней, направленных под углом -φ. Точки соединения их друг с другом и опорным шпангоутом, расположенным в начале отсчета продольной координаты, делят окружность шпангоута на равные дуги таким образом, что если стержни, расположенные под углом +φ, нумеровать i = 1,2…N, считая, что i возрастает по часовой стрелке, а стержни, направленные под углом -φ, против часовой соответственно нумеруются j = 1, 2, 3…N, то i-му стержню соответствует центральный угол 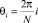 .
.
При этом существует связь j = N – i + 1.
Положим, что любой стержень с номером i в каркасе пересекается со стержнями `(не принимая в расчет точки соединения с опорными шпангоутами), направленными под углом -φ. Тогда точки пересечения (связи) делят его длину на равные участки K + 1.
Координаты точек пересечения соответственно равны 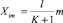 , m = 1, 2, 3,…K. При этом точка j соответствует пересечению стержня с номером і со стержнем, имеющим номер j = N – i – m + 1. Центральный угол
, m = 1, 2, 3,…K. При этом точка j соответствует пересечению стержня с номером і со стержнем, имеющим номер j = N – i – m + 1. Центральный угол 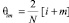 и координата этой точки по продольной оси каркаса
и координата этой точки по продольной оси каркаса 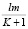 .
.
Функции динамической податливости изолированного стержня
Вынужденные колебания стержня постоянного сечения в пределах справедливости гипотезы плоских сечений и под действием единичной гармонической силы, приложенной в произвольной точке S по оси x, описываются, как известно, следующими уравнениями [2, 3]:
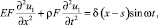
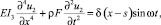
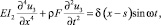 (8)
(8)
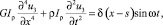
где E – модуль упругости; G – модуль сдвига; ρ – массовая плотность материала;
F – площадь поперечного сечения стержня; I2, I3 – моменты инерции сечений стержня относительно оси 2 и 3 соответственно; Iρ – полярный момент инерции; u1, u2, u3 – перемемещения в направлении оси 1, 2 и 3; u4 – угол закручивания относительно оси 1; δ(x – s) – разрывная функция Дирака 1-го рода.
Запишем граничные условия в виде
u1 = 0, 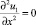 , u2 = 0,
, u2 = 0, 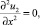 u3 = 0, (9)
u3 = 0, (9)
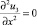 , u4 = 0 при x = 0, x = l.
, u4 = 0 при x = 0, x = l.
Будем искать решение (8) при
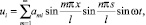 (10)
(10)
где
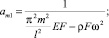
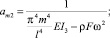
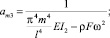 (11)
(11)
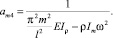
Основными элементами матрицы функции динамической податливости стержней будут амплитудные значения полученных перемещений, т.е.
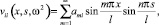 (12)
(12)
i = 1, 2, 3,………k.
Отличными от нуля являются также элементы υ55, υ66, υ35, υ53, υ62, υ26. Они определяются через основные, дифференциальными операциями.
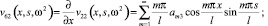
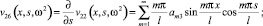
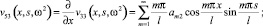 (13)
(13)
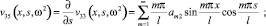
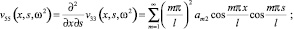
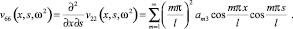
а)
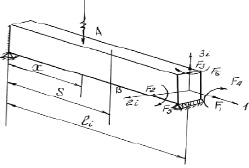
б)
Рис. 1. Расчетная схема оболочки: а) оболочка; б) стержневой элемент оболочки
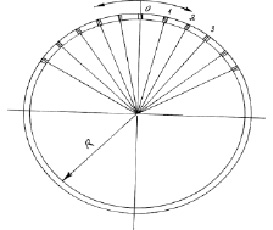
Рис. 2. Расположение стержней на опорном шпангоуте
В целом матрица функции динамической податливости прямого незакрученного стержня постоянного сечения имеет вид
 . (14)
. (14)
Функции динамической податливости стержней по направлениям осей 1, 2 и 3, совпадающих с осью каркаса, его радиусом и осью, расположенной в нормальном сечении под прямым углом к радиусу, обозначен через Гij(x, s, w2), где для простоты в индексах опущены штрихи.
Элементы матрицы Гij выражаются через vij следующим образом:
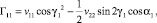
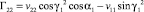 ,
,
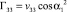 ,
,
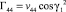 ,
,
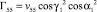 ,
,
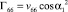 , (15)
, (15)
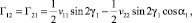
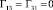 ,
, 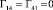 ,
, 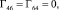
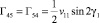 ,
,
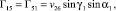
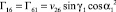 ,
,
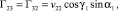
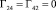 ,
,
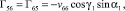
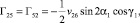
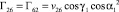 ,
,
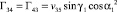 ,
,
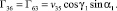
Функции динамической податливости стержневых элементов каркаса
Перемещения стержней с номерами і, работающих в составе каркаса, складываются из перемещений от действующей на них нагрузки и перемещений от реакции связанных с ним элементов каркаса, направленных под углом – φ к его оси, которые имеют вид
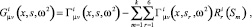 (16)
(16)
где 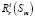 – реакция связей в точках Sm, k – число точек связи.
– реакция связей в точках Sm, k – число точек связи.
Амплитудные перемещения произвольного j-го элемента каркаса, направленного под углом -φ, равны.
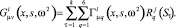 (17)
(17)
Из условий совместности перемещений элементов каркаса в точках связи получим
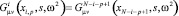 (18)
(18)
или
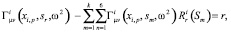
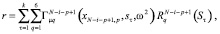
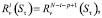 (19)
(19)
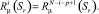
Раскроем выражение, подставив значения функции динамической податливости элементов каркаса:
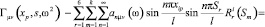
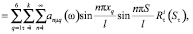 (20)
(20)
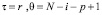 ;
; 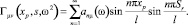
С целью дальнейшего упрощения (20) подставим координаты точек соединения стержней:
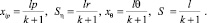 (21)
(21)
С учетом (21) функцию динамической податливости і-го стержня можем записать в виде
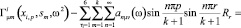
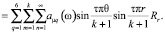 (22)
(22)
Так как синус является периодической функцией, то
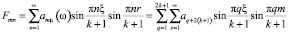 =
=
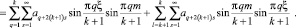 (23)
(23)
Пусть h = 2k + 2l, тогда
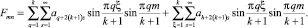 (24)
(24)
Из выражения (23) для amn следует
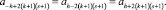 (25)
(25)
Таким образом
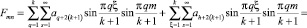
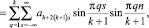 (26)
(26)
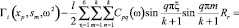
= 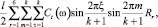 (27)
(27)
где
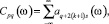
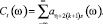 (28)
(28)
Теперь умножим левую и правую части нашего уравнения на 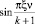 и просуммируем по ξ от 1 до k
и просуммируем по ξ от 1 до k
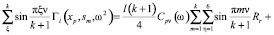
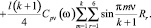 (29)
(29)
При этом использовались известные соотношения [1]:
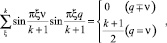 (30)
(30)
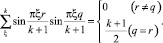
Это соотношение, иногда называемое свойством арифметической ортогональности, впервые было получено в работе [4] и использовано для решения задачи о колебаниях регулярных систем:
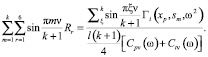 (31)
(31)
Вернемся к рассмотрению (16) с учетом (31), при этом выражение для функции динамической податливости стержня, соединенного со стержнем под углом φi, приобретает вид
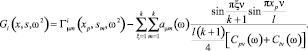 (32)
(32)
или, раскрыв выражение Гi(xp, sm, w2) по формуле (16), после некоторых преобразований, получим [5]:
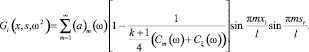 (33)
(33)
Заключение
Таким образом, будем считать решенной задачу о вынужденных колебаниях свободно опертого i-го стержня, соединенного со стержнями, направленными под углом –φ к оси α, так как амплитудные перемещения от произвольной нагрузки при известной ФДП могут быть определены интегральной сверткой G(x, s, w2) от функции нагрузки:
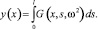 (34)
(34)
Библиографическая ссылка
Немеребаев М.Н., Бекмуратов М.М., Актаев Е.К. КОЛЕБАНИЯ КОМПОЗИЦИОННЫХ ОБОЛОЧЕК ТЕТРАСТРУКТУРЫ С УЧЕТОМ ДИСКРЕТНОСТИ ЭЛЕМЕНТОВ // Международный журнал прикладных и фундаментальных исследований. 2018. № 6. С. 30-37;URL: https://applied-research.ru/ru/article/view?id=12288 (дата обращения: 15.02.2026).
DOI: https://doi.org/10.17513/mjpfi.102288

