Введение
В работе [1] была описана квантовая структура поверхностного слоя R(I) атомно-гладких металлов (АГМ). Слой R(I) описывается уравнением Шредингера без привлечения внешних воздействий, то есть без внешней среды. В настоящей статье рассмотрен вопрос о поверхностном слое с учетом внешних воздействий, то есть в открытой квантовой системе, где не работают уравнения Шредингера, а работают уравнения Линдблада [2] и где эволюция матрицы плотности следует эффективному неэрмитову гамильтониану. Одним из явлений неэрмитовых систем является неэрмитов скин-эффект [3], а именно то, что большинство собственных состояний неэрмитового оператора локализованы на границах, что предполагает неблоховское соответствие объем – граница [4] и неблоховскую зонную теорию, основанную на обобщенной зоне Бриллюэна [5]. В статье рассмотрен раздел объем – межфазная граница АГМ, где формируется зона деформации со своей энергией Ed, которая описывается уравнением [6]:
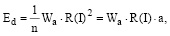 (1)
(1)
где Wa – энергия адгезии, а – постоянная кристаллической решетки.
Для АГМ энергия деформации Ed, определенная по формуле (1), показана в табл. 1.
Энергия деформации при внешнем воздействии расходуется на тепло, на акустоэмиссию (распространение звуковых волн), автоэлектронную эмиссию (испускание медленных электронов) и фрактолюминесценцию.
Цель исследования. В работе обсуждается превращение энергии деформации в другие виды энергии при внешних воздействиях на открытую квантовую систему поверхностного слоя атомно-гладких металлов.
Материалы и методы исследования
Объектом исследования являлись АГМ по Джексону [1]. Метод исследования включал уравнение (1) и формулы работы [1] и их сравнение с энергией Ферми электронного газа атомно-гладких металлов.
Результаты исследования и их обсуждение
Энергия деформации поверхностного слоя ненагруженных АГМ
Поверхностный слой R(I) металла имеет размеры от 1 до 6 нм [1], то есть представляет собой наноструктуру. В поверхностном слое R(I) происходят релаксация или реконструкция [7, с. 205] атомных монослоев (рис. 1).
Таблица 1
Энергия деформации Ed некоторых АГМ
|
АГМ |
Ed, (EF) эВ |
АГМ |
Ed, (EF) эВ |
АГМ |
Ed, (EF) эВ |
АГМ |
Ed, (EF) эВ |
|
Be |
15,61 (15,85) |
Cu |
7,68 (7,93) |
Mo |
7,16 (6,57) |
Re |
9,38 (10,80) |
|
Al |
11,73 (11,7) |
Ag |
5,64 (6,15) |
W |
12,23 (10,42) |
Fe |
12,0 (12,72) |
|
Si |
12,61 (8,84) |
Au |
6,10 (6,23) |
Mn |
9,73 (12,25) |
Co |
12,9 (13,22) |
|
Ge |
10,77 (8,09) |
Cr |
7,26 (7,80) |
Tc |
6,08 (9,91) |
Ni |
13,06 (13,22) |
Источник: составлено авторами.
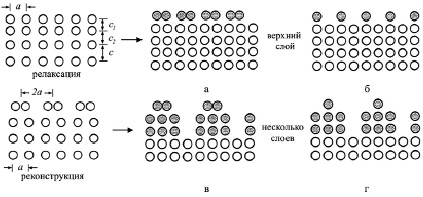
Рис. 1. Преобразование поверхности металла Источник: составлено авторами
У большинства металлов происходит релаксация поверхности. На поверхностях некоторых ГЦК металлов (например, Au, Ir и Pt), а также переходных ОЦК металлов (W и Mo) наблюдаются реконструкции [7, с. 205]. И релаксация, и реконструкция поверхности приводит к возникновению напряженно-деформируемых состояний, которые характеризуются энергий деформации металла Ed в ненагруженном состоянии (табл. 1).
Превращение энергии деформации в тепловую энергию электронного газа АГМ
Температура электронного газа в металле TF определяется энергией Ферми EF [8, с. 34] и равна TF = EF / kB, где kB = 8,6 10-5 эВ/К – постоянная Больцмана.
Энергия Ферми EF электронного газа определяется выражением
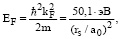 (2)
(2)
где kF – волновой вектор Ферми; rs – радиус сферы, приходящийся на один электрон проводимости; m – масса электрона; a0 – радиус атома водорода.
Значения энергии Ферми показаны в скобках в табл. 1 [9, с. 8, 10], а TF представлено в табл. 2.
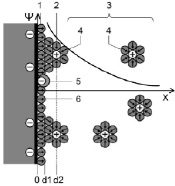
Из табл. 1 видно, что энергия EF ≈ Ed. Это означает, что на межфазной границе, то есть при z = R(I), собираются электроны с энергией деформации Ed, равной энергии Ферми EF, которая характерна для объемного (3D) металла. С термодинамической точки зрения такое равенство энергий означает равенство на межфазной границе химических потенциалов, что соответствует равновесию слоя R(I) (2D), погруженного в термостат объемного (3D) металла. Схему поверхностного слоя R(I) представим на рис. 2, а.
Из рис. 2, а, следует, что слой R(I) представляет собой двойной электрический слой (ДЭС), теория которого освещена в работах [11, с. 7, 12, 32] и на рис. 2, б. Слой R(I) представляет собой нелинейный конденсатор, из-за наличия размерных эффектов [1], и его схема похожа на работу [13, с. 124].
|
|
|
|
а) |
б) |
Рис. 2. Схема поверхностного слоя R(I) АГМ (а), схема ДЭС (б) Источник: составлено авторами по [11]
Таблица 2
Температура TF некоторых АГМ
|
АГМ |
TF, 104 К |
АГМ |
TF, 104 К |
АГМ |
TF, 104 К |
АГМ |
TF, 104 К |
|
Be |
6,34 |
Cu |
8,94 |
Mo |
12,5 |
Re |
10,9 |
|
Al |
9,08 |
Ag |
6,56 |
W |
14,2 |
Fe |
4,76 |
|
Si |
14,7 |
Au |
7,09 |
Mn |
11,7 |
Co |
4,57 |
|
Ge |
12,5 |
Cr |
5,63 |
Tc |
8,6 |
Ni |
4,50 |
Источник: составлено авторами.
Таблица 3
Собственная частота волн Лэмба для АГМ
|
АГМ |
λ = R(I), нм |
|
fo, ТГц (ETГц, эВ) |
АГМ |
λ = R(I), нм |
|
fo, ТГц (ETГц, эВ) |
|
Be |
0.8 (3) |
6400 |
8,00 (15,25) |
Mo |
1.8 (5) |
2700 |
1,50 (7,86) |
|
Al |
1.6 (4) |
3130 |
1,96 (14,81) |
W |
1.6 (5) |
2620 |
1,64 (9,86) |
|
Si |
2.1 (4) |
2200 |
1,05 (12,94) |
Mn |
1.1 (2) |
2575 |
2,34 (11,41) |
|
Ge |
2.4 (4) |
2700 |
1,13 (11,79) |
Tc |
1.4 (5) |
8100 |
5,79 (10,81) |
|
Cu |
1.2 (3) |
2260 |
1,88 (8,06) |
Re |
1.5 (5) |
2350 |
1,96 (8,91) |
|
Ag |
1.7 (4) |
1590 |
0,94 (5,23) |
Fe |
1.2 (3) |
3250 |
2,71 (10,78) |
|
Au |
1.7 (4) |
1200 |
0,81 (5,16) |
Co |
1.1 (3) |
2360 |
2,15 (9,58) |
|
Cr |
1.2 (4) |
2970 |
1,48 (6,68) |
Ni |
1.1 (3) |
2960 |
2,69 (10,19) |
Источник: составлено авторами.
Превращение энергии деформации в акустоэмиссию АГМ
На сегодняшний день известно несколько источников акустоэмиссии металлов: движение дислокаций; зарождение и рост трещин; процесс двойникования [14, с. 12]. Авторы добавляют в этот список превращение энергии деформации в акустоэмиссию. Поскольку слой R(I) представляет собой конечную 2D-наноструктуру, то здесь могут распространяться следующие типы волн: Лэмба; Рэлея; Стоунли и Лявы [15; 16]. Для микроэлектроники авторы применяют волны Лэмба и Явы [17; 18, с. 18], для горных пород и сейсмоакустики авторы применяют волны Рэлея и Стоунли [19; 20]. Для металлов в промышленности, в авиационной и ракетной технике авторы используют волны Лэмба [21; 22], теория которых продолжается до сих пор [23; 24].
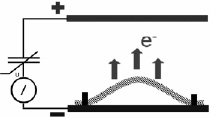
Рассмотрим волны Лэмба. Согласно работе [24] длина первой волны Лэмба равна толщине слоя, то есть λ = R(I). Для коротких волн длины волн равны λn = R(I) / n, где n – число монослоев (в скобках табл. 3). Авторы рассчитали собственную частоту 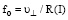 волны Лэмба для АГМ (табл. 3), где
волны Лэмба для АГМ (табл. 3), где 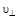 – скорость поперечной волны объемного металла.
– скорость поперечной волны объемного металла.
Из табл. 3 видно, что волны Лэмба в нанослое R(I) имеют собственную частоту fo в терагерцевом диапазоне, исследование которого начато недавно [25] и продолжается до сих пор [26; 27]. Кванту энергии E = h ∙ fo в 1 ТГц соответствует температура TTГц = 47,7 К. Тогда отношение температуры TF из табл. 2 к температуре TTГц даст число квантов суммарной энергии ETГц волн Лэмба. Такие расчеты представлены в скобках табл. 3, из которой следует ETГц ≈ EF ≈ Ed. Итак, энергия деформации превращается в акустоэмиссию при внешнем воздействии (лазерное облучение, ультразвук и пр.).
Превращение энергии деформации в автоэлектронную эмиссию АГМ
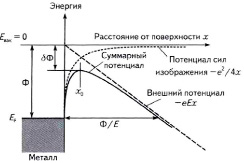
Для эмиссии электронов из металлов с атомно-гладкой поверхностью применяют теорию Фаулера – Нордгейма (рис. 3, а), формула которой выглядит так [28, с. 16]:
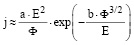 . (3)
. (3)
где j – плотность тока (А/см2), E – локальное электрическое поле у поверхности эмиттера (В/см), Ф – работа выхода (эВ), а, b – постоянные.
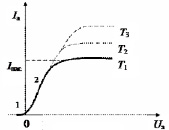
Вольт-амперная характериктика характерна для вакуумного диода и отвечает рис. 2, б. Теория Фаулера – Нордгейма хорошо описывает экспериментальные результаты для металлических эмиттеров в форме острия, когда его радиус больше 100 нм. Когда радиус эмиттера меньше 10 нм, то теория Фаулера – Нордгейма дает слишком завышенные результаты [28]. Авторами показано, что толщина поверхностного слоя R(I) АГМ составляет 1–6 нм. Автоэмиссия электронов из твердого тела используется при изготовлении автокатодов из различных материалов – вольфрама, молибдена, рения, платины, хрома, ниобия, гафния и различных полупроводников [29].
Величина работы выхода электронов для АГМ из рис. 3, а, равна Ф = W – EF и представлена в табл. 4 по результатам справочников [30].
|
|
|
|
а) |
б) |
Рис. 3. Потенциальная энергия электрона около металлической поверхности из-за наложения электрического поля напряженностью E. Суммарный потенциал (сплошная линия) складывается из потенциала сил изображения и внешнего потенциала, Ф – работа выхода без поля, ΔФ – изменение работы выхода с полем (а); вольт-амперная характеристика (б) Источник: составлено авторами
Таблица 4
Работа выхода электронов некоторых АГМ
|
АГМ |
Ф ∙ (2Ф), эВ |
АГМ |
Ф ∙ (2Ф), эВ |
АГМ |
Ф ∙ (2Ф), эВ |
АГМ |
Ф ∙ (2Ф), эВ |
|
Be |
3,9 (7,8) |
Cu |
4,4 (8,8) |
Mo |
4,2 (8,4) |
Re |
5,0 (10,0) |
|
Al |
4,2 (8,4) |
Ag |
4,7 (9,4) |
W |
4,6 (9,2) |
Fe |
4,7 (9,4) |
|
Si |
4,7 (9,4) |
Au |
4,8 (9,6) |
Mn |
4,0 (8,0) |
Co |
4,4 (8.8) |
|
Ge |
4,7 (9,4) |
Cr |
4,6 (9,2) |
Tc |
– |
Ni |
5,0 (10,0) |
Источник: составлено авторами.
Из сравнения табл. 4 с табл. 1 и 3 следует, что Ф = 0,5EF, так что порог эмиссии будет равен
δФ = 0,5EF / е ∙ R(I),
где е – заряд электрона. Знание величины δФ актуально для систем микроволновой связи, визуализации ИК-излучения, радиочастотной локации.
Превращение энергии деформации в фрактолюминесценцию АГМ
Фрактолюминесценция (ФЛ) – это излучение света от разрушения кристалла. Разрушение кристалла может происходить при трении, а излучение света при этом названо триболюминесценцией (ТЛ), которое является синонимом ФЛ. Существуют две основные точки зрения по поводу причин возникновения ФЛ и ТЛ [31]. Одни авторы относят ФЛ и ТЛ к газовому разряду между берегами растущих трещин, а другие – приписывают электронно-возбужденным свободным радикалам на берегах трещин. До настоящего времени дискуссия по возникновению ФЛ и ТЛ продолжается.
В работе [32] металлические мишени из платины, серебра и золота облучались лазером с тыльной стороны и измерялись фотоны люминесценции и электроны, испущенные из металла. Оказалось, что импульсы фотонов совпадают с импульсами электронов, то есть при деформации металлических мишеней одновременно происходит превращение энергии Ed в фрактолюминесценцию и автоэлектронную эмиссию электронов. Тогда длину фотонов для АГМ авторы данной статьи определяют аналогично, то есть 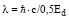 (табл. 5).
(табл. 5).
Видимый свет (380–750 нм) не включает в себя металлы Be, Al, Si, Ge, W, Fe, Co, Ni, а люминесценция их расположена в ультрафиолете. Фрактофотолюминесценция чистых металлов практически не исследована, поскольку свечение у них слабое и расположено у большинства из них вне видимой области спектра. Для цепочек из золота люминесценция исследовалась в работе [33] и показана на рис. 5.
Таблица 5
Длина волны максимума фрактолюминесценции АГМ
|
АГМ |
λ, нм |
АГМ |
λ, нм |
АГМ |
λ, нм |
АГМ |
λ, нм |
|
Be |
256 |
Cu |
521 |
Mo |
559 |
Re |
426 |
|
Al |
341 |
Ag |
609 |
W |
328 |
Fe |
333 |
|
Si |
318 |
Au |
556 |
Mn |
411 |
Co |
310 |
|
Ge |
368 |
Cr |
552 |
Tc |
667 |
Ni |
307 |
Источник: составлено авторами.
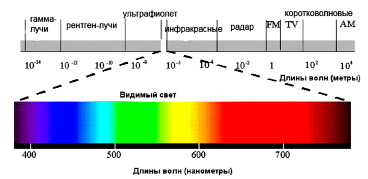
Рис. 4. Электромагнитный спектр (immunocap.ru)
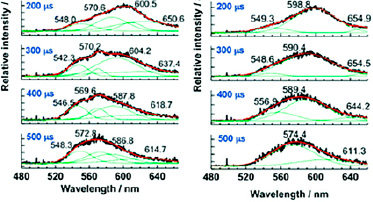
Рис. 5. Спектры люминесценции золота с временным разрешением и их кривые деконволюции (зеленые) при 77 К (λex = 355 нм) [33]
Чтобы сравнить данные табл. 5, приведем спектр электромагнитных волн (рис. 4).
Сравнение рис. 5 и табл. 5 приводит к выводу, что модель авторов данной статьи о превращении энергии деформации в люминесценцию чистых металлов при внешнем возбуждении верна.
Заключение
В статье показана исключительная роль поверхностного слоя чистых металлов, особенно его межфазной поверхности, где сосредоточена энергия деформации. При внешних воздействиях (ультразвук, электрическое или магнитное поле и пр.) энергия деформации становится источником акустоэмиссии, инжекции электронов и пр., то есть становится методом неразрушающего контроля металлических изделий.
Библиографическая ссылка
Юров В.М., Гончаренко В.И., Олешко В.С., Жангозин К.Н. ОТКРЫТАЯ КВАНТОВАЯ СИСТЕМА ПОВЕРХНОСТНОГО СЛОЯ АТОМНО-ГЛАДКИХ МЕТАЛЛОВ // Международный журнал прикладных и фундаментальных исследований. 2025. № 4. С. 54-60;URL: https://applied-research.ru/ru/article/view?id=13720 (дата обращения: 07.03.2026).
DOI: https://doi.org/10.17513/mjpfi.13720


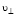 , м/с
, м/с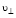 , м/с
, м/с