Введение
Вращательное движение широко и разнообразно представлено в природе и технике – от вращательных вибраций листьев растений и движения простейших организмов (например, Paramecium caudatum) до вращения многочисленных пропеллеров, винтов, турбин. К числу важных современных научно-технических задач с очевидностью относится задача синхронизации (или недопущения синхронизации) движения (в том числе вращательного движения) составных частей механических систем – задача организации (или предотвращения) движения составных частей механических систем по одному и тому же временному закону. Актуальность данной задачи определяется, в частности, тем, что синхронизация движения частей систем может быть причиной возникновения как желательных резонансов, так и вредоносных, способных приводить к тем или иным повреждениям и даже к разрушению аппаратов, устройств, конструкций. Задача синхронизации (или недопущения синхронизации) вращательного движения актуальна, в частности, для гидромеханических систем, подвергающихся периодическим по времени воздействиям. Изучение динамики гидромеханических систем при нестационарных (в том числе периодических) воздействиях является перспективным направлением в механике жидкости. Результаты исследований в этом научном направлении обладают как фундаментальным, так и прикладным содержанием [1–3]. В проводимых исследованиях используются экспериментальные и теоретические – аналитические, численные – методы. Исследованиям экспериментального типа посвящены, в частности, работы [4–6]. Результаты исследований с применением численных методов отражены в [7–9]. В работах [10–12] представлены примеры изучения вопросов с отчетливо выраженным прикладным содержанием. Современное состояние теоретических и экспериментальных исследований динамики гидромеханических систем при периодических по времени воздействиях адекватно характеризуется работами [13–15]. Краткий обзор ранее проведенных исследований содержится в [1].
Изучение вопросов, касающихся синхронизации движения в гидромеханических системах, начато в работе [3], где рассмотрен вопрос о синхронизации поступательного движения твердых частей системы с вязкой жидкостью. В данной работе поставлена и решена задача о вращательном движении гидромеханической системы с вязкой жидкостью, рассмотрен вопрос о синхронизации вращательного движения твердых частей системы.
Цель исследования – определение условий, при выполнении которых твердые части гидромеханической системы, подвергающейся внешнему периодическому силовому воздействию, совершают (или не совершают) синхронное вращательное движение.
Постановка и решение задачи о движении гидромеханической системы
Имеется гидромеханическая система, состоящая из несжимаемой вязкой жидкости и абсолютно твердых бесконечно длинных тел – криволинейной стенки η и криволинейной пластины ξ. Стенка η ограничена извне круговой цилиндрической поверхностью Γη радиуса Rη , ось которой находится на оси Z инерциальной прямоугольной системы координат X, Y, Z. Пластина ξ ограничена круговыми цилиндрическими поверхностями Γξ радиуса Rξ > Rη и Γ′ξ радиуса R′ξ > Rξ; оси поверхностей Γξ , Γ′ξ находятся на оси Z. Жидкость заполняет область Q : Rη < R < Rξ, 0 ≤ θ < 2π, –∞ < Z < ∞ (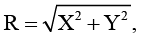
θ, Z – цилиндрическая система координат). Стенка и пластина совершают вращательное движение вокруг оси Z. Угловая скорость Ωη вращения стенки η вокруг оси Z заданным образом периодически с периодом T изменяется со временем 
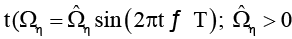– постоянная). Плотность пластины ξ не зависит от координаты Z. Пластина ξ является свободной – ее движение не задано, угловая скорость Ωξ вращения пластины ξ вокруг оси Z подлежит определению.
Пусть τ = t / T; r = R / Rη, rξ = Rξ / Rη; V, ρ, υ – соответственно скорость, плотность и кинематический коэффициент вязкости жидкости; eθ – единичный базисный вектор, направление которого совпадает с направлением возрастания угла θ;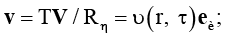 
P – давление в жидкости;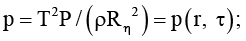 
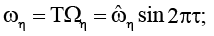ξ* – абсолютно твердое тело, часть пластины ξ, заполняющая область Q* : R ξ < R < R′ξ , 0 ≤ θ < 2π, Z* < Z < Z* + D (Z*, D > 0 – постоянные); I – момент инерции тела ξ* относительно оси Z; 
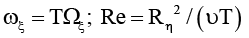– число Рейнольдса; 
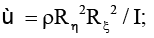Mliq – момент сил, действующих на тело ξ* со стороны жидкости, относительно оси Z; 
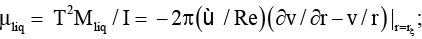Mext – момент внешних сил, действующих на тело ξ* , относительно оси Z; 
(
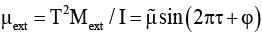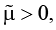0 ≤ ϕ < 2π – параметры).
Требуется определить движение гидромеханической системы (свободных частей системы – жидкости и пластины ξ).
Задачу о движении гидромеханической системы составляют уравнение движения пластины ξ (тела ξ* ) , уравнение Навье – Стокса и условия на твердых границах жидкости:
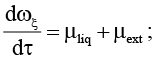(1)
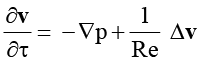в Q (2)
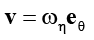на Гη; (3)
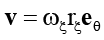на Гξ. (4)
Из (2)–(4) следует
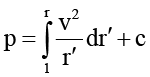(5)
(с – функция τ);
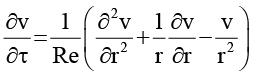для 1 < r < rξ; (6)
v = ωη при r = 1; (7)
v = ωξrξ при r = rξ. (8)
Сделаем в (6)–(8) подстановку
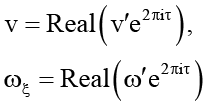, (9)
(v′– функция r ; ω′– постоянная). Используя полученные в результате этого соотношения, определим задачу
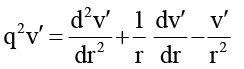для 1 < r < rξ; (10)
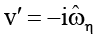при r = 1; (11)
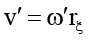при r = rξ. (12)
Здесь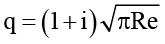 
. Задача (10)–(12) имеет решение
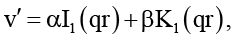(13)
где I1, K1 – модифицированные функции Бесселя;
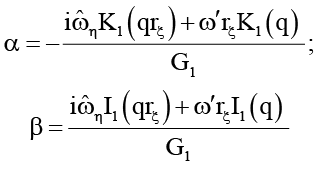
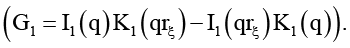
Используя (1), (9), (13), найдем
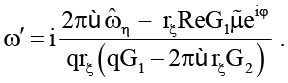(14)
Здесь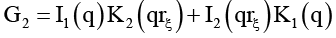 
(I2, K2 – модифицированные функции Бесселя).
Формулами (5), (9), (14) определяется точное решение задачи (1)–(4) о движении гидромеханической системы.
Результаты исследования и их обсуждение
Обратимся к вопросу о синхронизации движения твердых частей гидромеханической системы посредством внешнего силового воздействия на систему. Представим комплексную амплитуду ω′ в виде
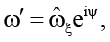(15)
где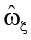 
и ψ – соответственно модуль и аргумент амплитуды ω′ (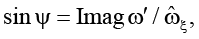
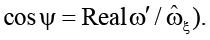Из (9), (15) следует
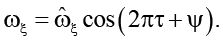(16)
Синхронность движения пластины ξ и стенки η состоит в том, что при любом значении τ имеет место равенство
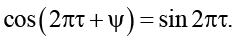(17)
Данное равенство (для любого τ ) выполняется тогда и только тогда, когда выполняются соотношения
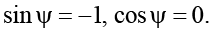(18)
Пусть значения числа Рейнольдса Re велики по сравнению с единицей. Используя (14), получим
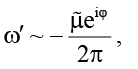sin ψ ~ – sin φ,
cos ψ ~ – cos φ при R → ∞. (19)
Согласно (18), (19) при больших значениях Re имеет место следующее. Пластина ξ и стенка η движутся синхронно, если управляющий параметр φ удовлетворяет условию
φ = π / 2 (20)
(если φ ≠ π / 2 синхронность отсутсвует). При выполнении (20) синхронное (с движением стенки η) движение пластины ξ происходит с угловой скоростью
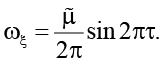
(амплитуда угловой скорости ωξ вращения пластины ξ зависит от управляющего параметра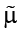 
). Внешнее силовое воздействие, обеспечивающее синхронное (с движением стенки η) движение пластины ξ, определяется формулой
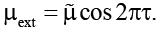
Пусть значения числа Рейнольдса Re малы по сравнению с единицей (Re > 0). Используя (14), пренебрегая величинами, малыми по сравнению с Re, получим
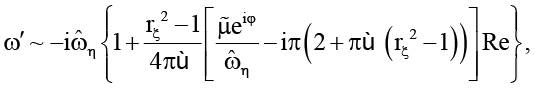
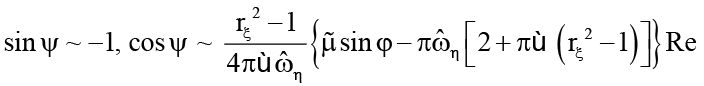при Re → 0 (21)
Согласно (18), (21) при малых значениях Re имеет место следующее.
1. В нулевом приближении (при учете только слагаемых, не зависящих от Re) пластина ξ и стенка η движутся синхронно, независимо от того, каков момент μext (независимо от значений параметров 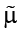, φ).
2. В первом приближении (при учете наряду со слагаемыми, не зависящими от Re, также слагаемых, пропорциональных Re) пластина ξ и стенка η движутся синхронно или несинхронно в зависимости от значений управляющих параметров 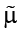, φ. При выполнении соотношения
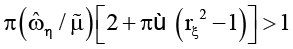
синхронность движения невозможна. Для значений управляющего параметра 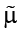, при которых имеет место соотношение
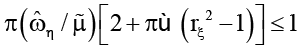
пластина ξ и стенка η движутся синхронно, если управляющий параметр φ удовлетворяет условию
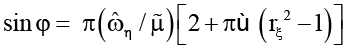(22)
(если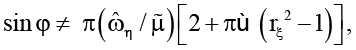 
синхронность отсутствует).
При выполнении (22) возможна реализация синхронного (с движением стенки η) движения пластины ξ с различными (безразмерными) угловыми скоростями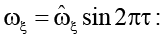 
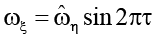для φ = π / 2
(угловые скорости вращения пластины ξ и стенки η совпадают);
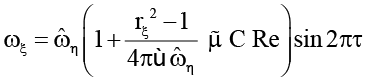
для 0 < φ < π / 2 (23)
(согласно (23)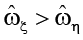 
(амплитуда угловой скорости вращения пластины ξ больше, чем амплитуда угловой скорости вращения стенки η));
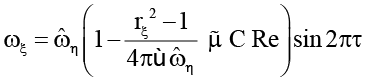
для π / 2 < φ < π (24)
(согласно (24)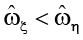 
(амплитуда угловой скорости вращения пластины ξ меньше, чем амплитуда угловой скорости вращения стенки η)).
Здесь
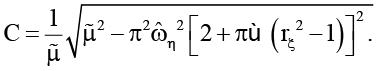
Точки границ Γη и Γξ стенки η и пластины ξ движутся по окружностям со скоростями
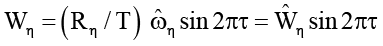
и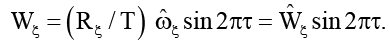
Согласно (24), при том что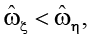 
имеют место формулы
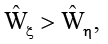если Н < 1
(при всех значениях τ, кроме τ = 0, 1, –1, 2, –2, … , точки границы Γξ пластины ξ обгоняют точки границы Γη стенки η);
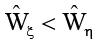если Н > 1
(при всех значениях τ, кроме τ = 0, 1, –1, 2, –2, … , точки границы Γξ пластины ξ отстают от точек границы Γη стенки η);
Wξ = Wη, если Н = 1
(при всех значениях τ скорости движения точек границ Γξ и Γη по окружностям совпадают).
Здесь
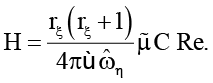
Внешнее силовое воздействие, обеспечивающее синхронность движения пластины ξ и стенки η, определяется формулами
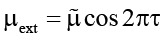для φ = π / 2;
для 0 < φ < π / 2;
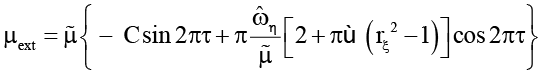для π / 2 < φ < π.
Заключение
В работе рассмотрена новая задача о вращательном движении гидромеханической системы с вязкой жидкостью в присутствии внешнего периодического по времени силового воздействия на систему. Найдено точное решение задачи. Проанализирована динамика системы при больших и малых значениях числа Рейнольдса. Установлена возможность синхронизации вращательного движения твердых частей гидромеханической системы посредством внешнего периодического воздействия. Сформулированы условия, при выполнении которых твердые части гидромеханической системы совершают (или не совершают) синхронное вращательное движение. Обнаружено, что требование синхронности вращательного движения твердых частей системы не является достаточным для однозначного определения вращательного движения свободной твердой части гидромеханической системы.
Результаты работы могут использоваться, в частности, при поиске новых, перспективных подходов к решению актуальных научно-технических проблем.
Конфликт интересов
Библиографическая ссылка
Сенницкий В.Л. О ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ ГИДРОМЕХАНИЧЕСКОЙ СИСТЕМЫ С ВЯЗКОЙ ЖИДКОСТЬЮ // Международный журнал прикладных и фундаментальных исследований. 2025. № 9. С. 37-41;URL: https://applied-research.ru/ru/article/view?id=13757 (дата обращения: 09.10.2025).
DOI: https://doi.org/10.17513/mjpfi.13757