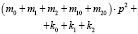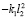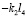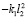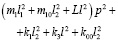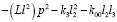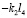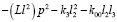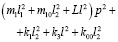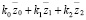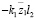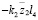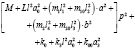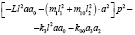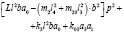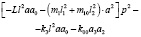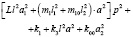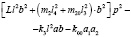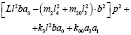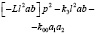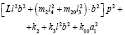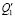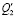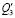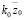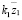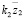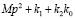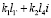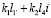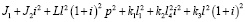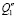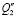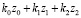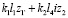Внимание к задачам динамики транспортных средств инициируется развитием мобильной робототехники и использованием управляемых виброзащитных систем [1 ÷ 4]. Ряд вопросов, связанных с особенностями построения математических моделей колебательных систем, рассмотрен в монографиях [5, 6], что предопределило интерес к развитию методологического базиса теории и практики виброзащиты, а также – к поиску новых способов и средств оценки изменения и управления динамическим состоянием систем, содержащих не только упругие и диссипативные элементы, но и устройства для преобразования движения, в том числе и рычажные механизмы различных видов [5, 7 ÷ 9]. Вместе с тем, введение рычажных механизмов в структуры колебательных систем связано с необходимостью учета многочисленных особенностей, которые возникают при выборе места расположения точек опоры рычагов, их конфигурации и форм использования соединительных элементов.
В предлагаемой статье рассматриваются возможности построения математических моделей подвесок мобильных робототехнических систем, в составе которых используются сложные рычажные связи, а также особенности возникающих режимов и условий формирования динамического состояния.
I. Общие положения. Постановка задачи
Рассматривается система, которая имеет объект защиты массой m0, совершающий вертикальные движения (у0) относительно положения статического равновесия: в тт. А и В к объекту защиты прикрепляются два рычажных механизма обратной Т-образной формы.
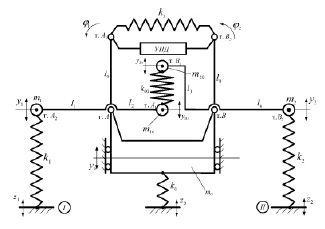
Рис. 1. Расчетная схема блока подвески робототехнического устройства
Каждый из рычажных механизмов имеет массоинерционные элементы, закрепленные соответственно в тт. А2, А1 (m1 , m10) и тт. В2, В1 (m2, m20). В тт. А3, В3 закреплены элементы системы: пружина жесткостью k3 и устройство для преобразования движения (УПД) в виде винтового несамотормозящегося механизма [10]. Кроме того, точки А1 и В1 связаны упругим элементом жесткостью k00. В свою очередь, объект также опирается на пружину жесткостью k0.
Массоинерционные элементы m1 и m2 опираются на опорные поверхности I и II, закон движения которых известен (z1, z2). Кроме того, элемент k0 опирается на опорную поверхность с законом движения z0(t). Предполагается, что система совершает малые колебания без учета сил сопротивления. Для описания движения используются системы координат у0, φ1, φ2 и у0, у1, у2. Все необходимые геометрические параметры показаны на рис. 1.
Кинематические возмущения на стадии предварительного изучения считаются гармоническими. Вопросы взаимоотношения параметров движения z0, z1, z2 рассматриваются отдельно.
Цель исследования заключается в оценке динамических свойств системы, возникающих при действии гармонических сил, которые могут находиться между собой в определенных соотношениях.
В числе решаемых задач предполагается разработка математической модели системы и оценке возможностей изменения динамического состояния путем структурных трансформаций и выбора настроечных параметров.
II. Построение математической модели системы
Используются структурные методы математического моделирования [6, 9 ÷ 11]. Запишем выражения для кинетической и потенциальной энергий в предположении, что система совершает малые колебания относительно положения статического равновесия:
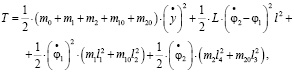 (1)
(1)
где φ1 и φ2 – углы поворота рычажных устройств относительно объекта m0; L – приведенная массоинерционная характеристика УПД [10];
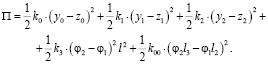 (2)
(2)
Для определения производных от потенциальной энергии введем ряд соотношений:
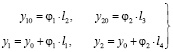 (3)
(3)
С учетом соотношений (3) потенциальная энергия запишется:
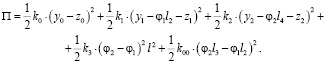 (4)
(4)
Тогда:
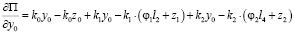 .
.
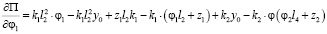 .
.
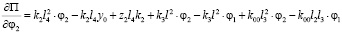 .
.
Найдем уравнения движения:
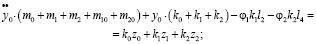 (5)
(5)
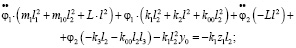 (6)
(6)
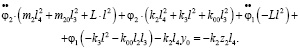 (7)
(7)
На рис. 2 приведена структурная схема исходной системы (рис. 1) в координатах у0, φ1, φ2. Особенность системы заключается в том, что между парциальными системами (φ1) и (φ2) связь имеет инерционно-упругий тип. При частоте внешнего воздействия:
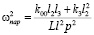 , (8)
, (8)
возможно обнуление межпарциальных связей между φ1 и φ2 (а также между у1 и у2). В остальных случаях, то есть при рассмотрении у0 и φ1, а также φ2 и у0, связи являются упругими.
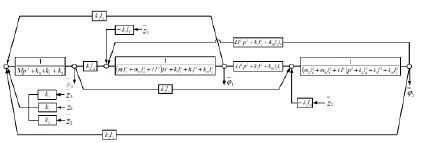
Рис. 2. Структурная схема системы с Т-образными рычагами (рис. 1) в координатах 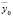 ,
, 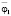 ,
, 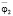
В табл. 1 приведены коэффициенты уравнений движения (5)–(7) в координатах у0, φ1, φ2.
Таблица 1
Коэффициенты уравнений (5) ÷ (7)
|
а11 |
а12 |
а13 |
|
|
|
|
|
а21 |
а22 |
а23 |
|
|
|
|
|
а31 |
а32 |
а33 |
|
|
|
|
|
Q1 |
Q2 |
Q3 |
|
|
|
|
Примечание. В таблице представлены результаты преобразования (5) ÷ (7) по Лапласу (p =jω – комплексная переменная [10, 11]; Q1 ÷ Q3 – обобщенная сила по координатам у0, 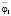 и
и 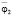 .
.
III. Оценка динамических свойств системы
Для оценки динамических свойств системы могут быть использованы формулы Крамера [12].
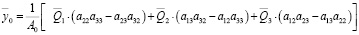 , (9)
, (9)
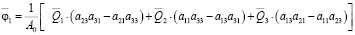 , (10)
, (10)
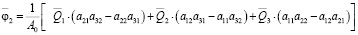 , (11)
, (11)
где А0 – характеристическое уравнение системы, приведенной на рис. 2.
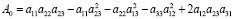 . (12)
. (12)
Используя формулы (10) ÷ (12) , можно найти передаточные функции, определяющие взаимодействие между входными внешними возмущениями из набора 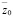 ,
, 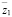 ,
, 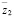 и выходными сигналами
и выходными сигналами 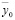 ,
, 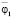 ,
, 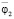 . Если на входе в парциальную систему действует несколько сигналов, как, это следует, к примеру, из табл. 1 по отношению к объекту защиты m0, то может быть использован принцип суперпозиции. Определенный интерес представляет рассмотрение ситуации, при которой между внешними сигналами z0, z1, z2 устанавливаются некоторые соотношения. Например, можно предполагать, что система опирается одновременно на одну поверхность, тогда можно принять, что
. Если на входе в парциальную систему действует несколько сигналов, как, это следует, к примеру, из табл. 1 по отношению к объекту защиты m0, то может быть использован принцип суперпозиции. Определенный интерес представляет рассмотрение ситуации, при которой между внешними сигналами z0, z1, z2 устанавливаются некоторые соотношения. Например, можно предполагать, что система опирается одновременно на одну поверхность, тогда можно принять, что 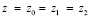 – с соответствующими особенностями определения передаточных функций на основе выражений (10) ÷ (12).
– с соответствующими особенностями определения передаточных функций на основе выражений (10) ÷ (12).
Если k0 = 0, то объект m0 непосредственно не связан с опорной поверхностью, контакт осуществляется через упругие элементы k1 и k2 (рис. 1). При 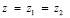 можно получить передаточную функцию при входном сигнале (или обобщенном внешнем воздействии
можно получить передаточную функцию при входном сигнале (или обобщенном внешнем воздействии 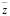 ) и выходном сигнале
) и выходном сигнале 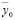 :
:
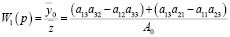 . (13)
. (13)
Так как а23 в соответствии со структурной схемой на рис.2 и табл. 1 имеет вид:
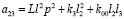 , (14)
, (14)
то числитель (13) при
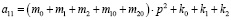 (15)
(15)
представляет собой биквадратное уравнение относительно квадрата частоты внешнего воздействия. Если исключить контакт m0 с опорной поверхностью, приняв k0 = 0, то в отношении объекта защиты можно ожидать появления двух режимов динамического гашения колебаний при действии вибраций со стороны основания (z = z1 = z2). Ситуация, в принципе, не изменится, если будет выполняться условие 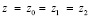 (k0 ≠ 0). Однако при этом параметры (то есть частоты динамического гашения) изменятся. Амплитудно-частотные характеристики системы по переменной
(k0 ≠ 0). Однако при этом параметры (то есть частоты динамического гашения) изменятся. Амплитудно-частотные характеристики системы по переменной 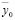 будут иметь обычный характер. Отметим, что при характеристическом уравнении А0 можно ожидать наличие трех резонансных частот с соответствующим увеличением амплитуд колебаний по координате у0. В этом случае две частоты динамического гашения будут располагаться между тремя резонансными частотами. Схема подвески (рис. 1) обладает возможностями изменения динамического состояния объекта защиты m0 путем соответствующего выбора настроечных параметров. Такими параметрами могут стать длины звеньев рычагов, жесткости упругих элементов k3 и k00, а также массоинерционные параметры УПД (имеются в виду L – приведенная масса УПД и l – длина плеча рычага). Выше отмечалось, что при соблюдении соотношения (8) возможна развязка парциальных связей.
будут иметь обычный характер. Отметим, что при характеристическом уравнении А0 можно ожидать наличие трех резонансных частот с соответствующим увеличением амплитуд колебаний по координате у0. В этом случае две частоты динамического гашения будут располагаться между тремя резонансными частотами. Схема подвески (рис. 1) обладает возможностями изменения динамического состояния объекта защиты m0 путем соответствующего выбора настроечных параметров. Такими параметрами могут стать длины звеньев рычагов, жесткости упругих элементов k3 и k00, а также массоинерционные параметры УПД (имеются в виду L – приведенная масса УПД и l – длина плеча рычага). Выше отмечалось, что при соблюдении соотношения (8) возможна развязка парциальных связей.
В подвесках с рычажной связями при наличии нескольких входных сигналов возможны проявления локальных зависимостей между внешними воздействиями. К примеру, соотношения 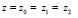 отражают возможность вертикальных колебаний одновременно всех опорных поверхностей одновременно. Однако, вполне возможными являются ситуации, когда движения по отдельным поверхностям (z0, z1, z2) рассматриваются как фрагменты некоторого общего движения. Таким движением может быть качание общей поверхности относительно некоторого центра и др. В спектральной теории подвески транспортных систем рассматриваются более сложные функциональные зависимости между действиями нескольких входных сигналов. В работах [13, 14] рассматриваются возможности линейных соотношений в параметрах одновременно действующих возмущений. Отметим также, что возникающая постановка задачи оценки динамического состояния системы при действии нескольких силовых факторов может считаться вполне «естественной» при действии внешней силы, смещенной относительно центра тяжести, при колебаниях, например, твердого тела на упругих опорах, совершающего плоские колебания.
отражают возможность вертикальных колебаний одновременно всех опорных поверхностей одновременно. Однако, вполне возможными являются ситуации, когда движения по отдельным поверхностям (z0, z1, z2) рассматриваются как фрагменты некоторого общего движения. Таким движением может быть качание общей поверхности относительно некоторого центра и др. В спектральной теории подвески транспортных систем рассматриваются более сложные функциональные зависимости между действиями нескольких входных сигналов. В работах [13, 14] рассматриваются возможности линейных соотношений в параметрах одновременно действующих возмущений. Отметим также, что возникающая постановка задачи оценки динамического состояния системы при действии нескольких силовых факторов может считаться вполне «естественной» при действии внешней силы, смещенной относительно центра тяжести, при колебаниях, например, твердого тела на упругих опорах, совершающего плоские колебания.
Использование настроечных параметров k3 и k00 в рассматриваемой схеме (рис. 1) обладает вполне определенными недостатками. В частности, при k00 → ∞ связь между элементами m10 и m20 блокируется, что одновременно приводит к блокированию относительного движения рычагов (по отношению к объекту защиты m0). Большими возможностями, в этом плане, обладают подвески с возможностями зубчатого зацепления рычажных устройств.
IV. Особенности динамических свойств системы в координатах у0, у1, у2
Для построения математической модели системы введен ряд соотношений:
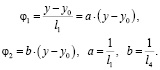 (16)
(16)
Запишем выражения для кинетической и потенциальной энергий:
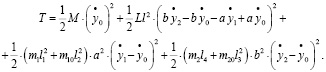 (17)
(17)
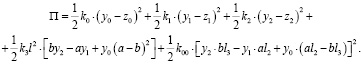 (18)
(18)
Введем ряд обозначений:
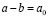 ,
, 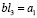 ,
, 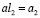 ,
, 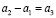 . (19)
. (19)
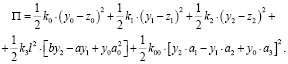 (20)
(20)
Построим систему уравнений движения в координатах у0, у1, у2.
Пусть
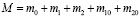 . (21)
. (21)
Запишем уравнения движения в координатах у0, у1, у2:
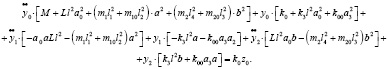 (22)
(22)
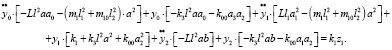 (23)
(23)
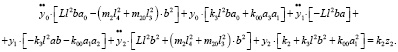 (24)
(24)
В табл. 2 приведены коэффициенты уравнений системы в координатах у0, у1. у2.
Таблица 2
Коэффициенты уравнений в координатах у0, у1. у2
|
а11 |
а12 |
а13 |
|
|
|
|
|
а21 |
а22 |
а23 |
|
|
|
|
|
а31 |
а32 |
а33 |
|
|
|
|
|
|
|
|
|
|
|
|
Примечание. 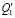 ,
, 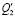 ,
, 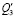 – обобщенные силы соответствуют обобщенным координатам у0, у1. у2.
– обобщенные силы соответствуют обобщенным координатам у0, у1. у2.
Анализ свойств системы с использованием (9) – (12) может быть построен на передаточной функции вида:
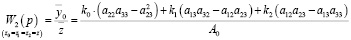 . (25)
. (25)
Из (25) могут быть получены условия возникновения режимов динамического гашения по координате 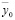 при различных соотношениях параметров. Поскольку наблюдаемая координата у0 в системе координат у0, φ1, φ2 и
при различных соотношениях параметров. Поскольку наблюдаемая координата у0 в системе координат у0, φ1, φ2 и 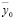 ,
, 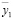 ,
, 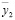 одинакова, то и частоты динамического гашения будут одинаковыми.
одинакова, то и частоты динамического гашения будут одинаковыми.
Вместе с тем, при анализе (25) значения коэффициентов аij должны браться из табл. 2. Что касается характеристического уравнения, то его то его общая схема построения остается неизменной, однако при переходе от системы координат у0, φ1, φ2 к системе у0, у1. у2 между характеристическими уравнениями будут формироваться постоянные множители, определяющие согласование размерностей переменных состояния (линейные и угловые).
V. Учет особенностей зубчатого соединения рычажных секторов
Рассматривается система с двумя степенями свободы, как показано на рис. 3.
В схеме (рис. 3) реализуется зубчатое зацепление, что обеспечивает связь угловых скоростей вращения φ1 и φ2:
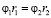 ,
, 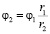 ;
;
при этом вращения происходят в разных направлениях. Выражение для потенциальной энергии имеет вид:
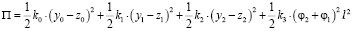 . (26)
. (26)
Последний член выражения (26) может быть преобразован:
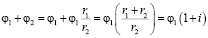 .
.
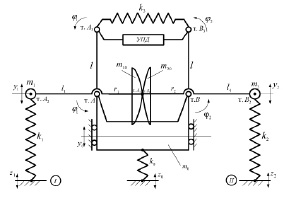
Рис. 3. Расчетная схема системы с зубчатой передачей в контакте двух рычажных секторов
Тогда потенциальная энергия системы определится:
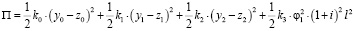 . (27)
. (27)
Рычажные сектора имеют массоинерционные свойства:
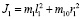 ; (28)
; (28)
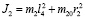 . (29)
. (29)
Выражение для кинетической энергии системы имеет вид:
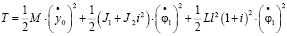 . (30)
. (30)
Так как:
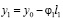 ;
; 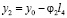 ,
,
то в общем виде:
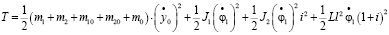 . (31)
. (31)
Сделаем ряд промежуточных выкладок:
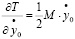 ;
; 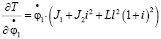 .
.
Запишем ряд соотношений:
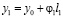 ;
; 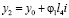 ;
; 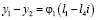 ;
;
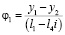 . (32)
. (32)
Таким образом, потенциальная энергия системы определится:
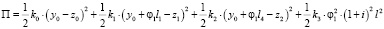 . (33)
. (33)
Сделаем ряд вспомогательных преобразований и запишем уравнения движения системы в координатах у0 и φ1:
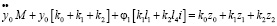 . (34)
. (34)
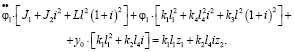 (35)
(35)
Коэффициенты уравнений (34), (35) приведены в табл. 3.
Таблица 3
Коэффициенты системы уравнений в координатах у0, φ1
|
а11 |
а12 |
|
|
|
|
а21 |
а22 |
|
|
|
|
|
|
|
|
|
Примечание. 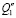 ,
, 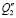 – обобщенные силы, соответствующие координатам у0 и φ.
– обобщенные силы, соответствующие координатам у0 и φ.
На рис. 4 приведена структурная схема системы в координатах у0 и φ. В этой системе межпарциальные связи носят упругий характер.
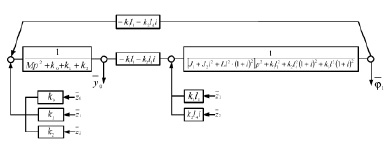
Рис. 4. Структурная схема системы (рис. 1) с зубчатыми секторами
Пусть z1 = 0, z2 = 0. Тогда передаточная функция примет вид:
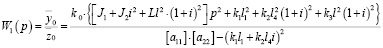 . (36)
. (36)
Из (36) можно определить частоту динамического гашения (z0 = z; z1 = 0; z2 = 0):
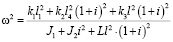 . (37)
. (37)
Аналогичным образом могут быть найдены и другие режимы динамического гашения, возникающие при различных вариантах сочетания внешних воздействий.
Возможности настройки системы определяются параметрами системы: жесткостью k3, длинами плеч рычагов (l), передаточным отношением i и массо-инерционными свойствами зубчатых секторов. Отметим, что система имеет две резонансные частоты (или частоты собственных колебаний), которые могут быть найдены из характеристического уравнения (36).
Заключение
Таким образом, механическая система с рычажными связями, рассматриваемая в динамических взаимодействиях с вибрирующим основанием обладает расширенным набором адаптационных свойств. При обеспечении упругой связи k00 между настроечными массами (m1, m2, m10, m20) система может иметь два режима динамического гашения. В качестве настроечных параметров могут выступать жесткость пружины k3 и инерционные свойства УПД (через Ll2).
При введении зубчатой передачи между рычажными секторами система теряет одну степень свободы, однако адаптационные возможности в гашении внешних кинематических воздействий могут быть поддержаны введением передаточных отношений между рычажными секторами и выбором других настроечных параметров.
1. Предлагается метод построения и анализа динамических свойств системы на основе математических моделей, построенных с учетом рычажных связей, реализуемых рычажными секторами.
2. Рычажные сектора могут рассматриваться как новый элемент механических колебательных систем, обладающий расширенными возможностями динамических воздействий, в частности, из-за простоты применения и использования активных средств приложения управляемых моментов сил для изменения динамического состояния.
Библиографическая ссылка
Елисеев С.В., Трофимов А.Н., Каимов Е.В. КОНСТРУКТИВНО-ТЕХНИЧЕСКИЕ ФОРМЫ ИСПОЛЬЗОВАНИЯ РЫЧАЖНЫХ СВЯЗЕЙ В ЗАДАЧАХ ДИНАМИКИ ПОДВЕСОК ТРАНСПОРТНЫХ СРЕДСТВ // Международный журнал прикладных и фундаментальных исследований. 2014. № 5-2. С. 14-23;URL: https://applied-research.ru/ru/article/view?id=5328 (дата обращения: 03.03.2026).