Для получения надежных и экономичных несущих конструкций машин и механизмов необходима разработка прогрессивных методов расчета с учетом использования новейших вычислительных и программных средств.
Наличие на сегодняшний день на рынке программных продуктов коммерческих версий систем автоматизированного проектирования (AutoCAD, CATIA, ProEngineering и др.) и анализа (ADAMS, Cosmos/M, ANSYS, NASTRAN и др.) требует их обоснованного выбора для решения конкретной проблемы, а также создания гибкого интерфейса между двумя указанными классами программного обеспечения [1].
Предлагается новый системный подход на основе поэтапного использования CAD/CAE/CAM – систем, в рамках которого предложены процедуры: проектирования с использованием геометрического моделирования; прочностного анализа на основе концепции «соответствие назначению»; эскизного проектирования и выработки рекомендаций для построения технологических процессов.
Развитие средств вычислительной техники стимулировало распространение инженерного анализа практически на все этапы проектирования машиностроительных технологий и изделий. Многообразие физических процессов в наукоемких изделиях, субъективность в постановке задач анализа, выбор методов решения и многие другие причины привели к огромному числу методик, алгоритмов и программ, предназначенных для решения задач анализа машиностроительных изделий [2].
Основные положения предлагаемого подхода:
- Определение ожидаемых нагрузок на узлы и элементы осуществляются на основе макроанализа конструкции пространствееного манипулятора, представленной как система с дискретно-распределенными параметрами.
- Учет технологических факторов реализуется на микроуровне путем описания реальной геометрии соединений элементов манипулятора и конкретной технологии их исполнения (сварки и т.п.).
- Конструкционное соответствие реального изделия и его модели реализуется на основе применения численных методов анализа.
- Предельное состояние в момент исчерпания несущей способности при действии статических и динамических нагрузок оценивается на основе многопараметрических критериев прочности.
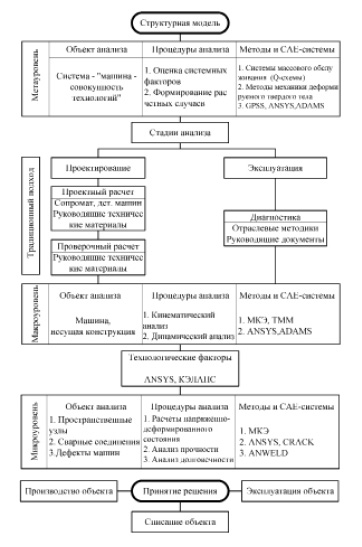
Рис. 1. Блочно-иерархический подход
Кинематический и динамический анализ манипулятора с использованием системы ADAMS
На первом этапе создается модель манипулятора в модуле ADAMS/View.
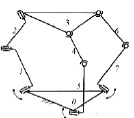
Рис. 2. Схема манипулятора
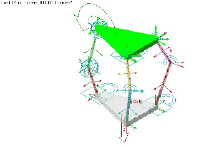
Рис. 3. Модель манипулятора, построенная в системе ADAMS
ADAMS предоставляет возможность получения значений кинематических и динамических характеристик, таких как скорость, ускорение, угловая скорость, угловое ускорение, кинетическая и потенциальная энергии, силы, моменты, общую силу на точку и т.д.
Взаимодействие пакетов макро-микроанализа
Несмотря на множество достоинств ADAMS имеет небольшой недостаток, все элементы анализируемых моделей являются жесткими. Однако для решения этой проблемы, система предоставляет возможность обмениваться данными с конечно-элементными системами. Система ANSYS позволяет создавать *.mnf файл (modal neutral file), который в дальнейшем импортируется в ADAMS.
Этапы взаимодействия ANSYS-ADAMS:
- Построение модели (возможно как непосредственно в системе ANSYS, так и в системе ADAMS с дальнейшим экспортом модели). ADAMS предоставляет возможность экспорта модели или элементов модели в различные форматы, поддерживаемые конечно-элементными системами (IGES, SAT, Parasolid, STEP и т.д.)
- Моделирование необходимых точек
- Экспорт в ADAMS (создание .mnf файла)
- Проведение анализа в ADAMS с использованием .mnf файла.
- Передача результирующих данных из ADAMS в ANSYS, проведение статического анализа.
При создании модели, которая будет в дальнейшем экспортироваться в ADAMS, необходимо большое внимание уделить созданию и выбору узлов (точек), так как в ADAMS силы прикладывают к точкам структуры, а также шарниры закрепляются в указанных точках.
Поскольку алгоритм основан на методе синтеза мод компонента, или «динамическом подструктурировании» рассматриваются только линейные свойства. ADAMS использует «подход Крейга Бемптона» с некоторыми модификациями[].
Все геометрические и физические нелинейности игнорируются. Если в модели присутствуют существенные геометрические нелинейные эффекты, необходимо разбить компонент на несколько небольших и рассматривать каждую часть отдельно. Затем можно собрать подразделенные компоненты в ADAMS, чтобы сформировать гибкий компонент с геометрической нелинейностью.
Был произведен экспорт элементов модели манипулятора в формат Parasolid для передачи в систему ANSYS. После импорта твердотельного элемента в конечно-элементную систему была создана деформируемая модель элемента конструкции (элемент разбит на конечные элементы Solid45, Beam4).
Используя средства передачи данных обратно в систему ADAMS была подготовлена модель и создан соответствующий mnf файл. С помощью также встроенных средств деформируемые элементы были вновь импортированы в ADAMS для повторного проведения динамического, кинематического анализов и уточнения расчетного случая и усилий.
Контактные напряжения в элементах пространственных шарнирных узлов
Шарнирные узлы, как правило, являются наиболее ответственными и наименее долговечными элементами конструкции. Основным критическим элементом шарнирного узла является проушина, имеющая очень низкий предел выносливости по сравнению с пределом выносливости самого материала. Природа этого явления заключается в высоком уровне концентрации напряжений около нагруженного отверстия, где в зоне максимальных окружных напряжений имеет место коррозия трения (фреттинг-коррозия), связанная с механическим истиранием поверхностей [2].
Решение задачи проводилось в уточненной нелинейной постановке с учетом упругопластического деформирования материала и контактного взаимодействия поверхностей деталей. Решение нелинейных задач осуществляется шагово-итерационным методом последовательных нагружений. Для описания пластического поведения использовалась билинейная модель с кинематическим упрочнением, которая справедлива для большинства металлов в случае небольших пластических деформаций [3].
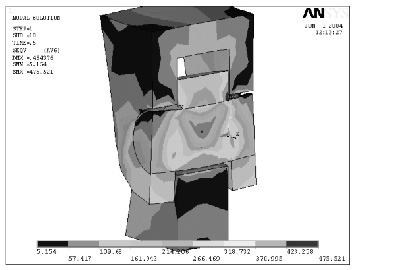
Рис. 4. Напряженно-деформированное состояние модели
Можно наблюдать изгиб оси, который влечет за собой сложную деформацию вильчатой проушины и контактную деформацию смятия центральной проушины. Максимальные напряжения растяжения, равные 429 МПа, наблюдаются в нижней части оси и вызваны изгибающим моментом.
Результаты проведенных исследований показали, что даже при приложении небольшой нагрузки в зоне отверстий проушин возникают значительные напряжения, превышающие предел допустимых. Также были рассмотрены способы уменьшения величины контактных напряжений с использованием технологических факторов (посадка оси с натягом, установка вильчатой проушины под углом к центральной проушине).
Эта технология найдет применение на всех стадиях жизненного цикла изделий – в проектировании, в производстве и эксплуатации, для изучения предельных возможностей машин, обеспечения ресурса и безопасности конструкции и обеспечит экономическую эффективность, без которой невозможен успех в новых условиях рыночной экономики.
Задачи механики разрушения сварных конструкций
Значительная часть повреждений несущих металлоконструкций манипулятора обусловлена усталостью сварных соединений. Стремление к наиболее полному использованию прочностных свойств материалов и соединений привело к тому, что сварные конструкции по сопротивлению усталости стали приближаться к предельным состояниям, а в ряде случаев превышают их.
Использование современных методов автоматизированного анализа для решения задач механики разрушения позволяет комплексно учесть целый ряд факторов, способных существенно повлиять на результаты анализа [4].
Были рассмотрены образцы, моделирующие поведение основных типов сварных соединений. Используя программу ANSYS, получены значения коэффициента интенсивности напряжений. С помощью программного пакета нетрадиционного математического моделирования многомерных зависимостей ANETR определены регрессионные зависимости и статистические характеристики.
Влияния остаточных напряжений на величину коэффициента интенсивности напряжений в сварных соединениях, выполненных короткими швами, оценивается с помощью полученных регрессионных зависимостей. При определении регрессионных зависимостей коэффициента интенсивности остаточных напряжений использовались три фактора: a – коэффициент, оценивающий уровень остаточных напряжений, где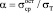 
, 
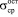– остаточные нерелаксированные усредненные напряжения, нормальные к берегу трещины при ее отсутствии; 
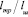– отношение длины трещины к длине шва; 
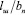– отношение длины шва к ширине зоны, нагревающейся до температуры, при которой предел текучести металла близок к нулю.
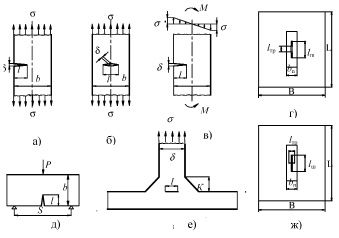
Рис. 5. Расчетные схемы стандартных образцов: а – образец с одной краевой трещиной; б – образец с центральной трещиной; в – чистый изгиб полосы с краевой трещиной; г – центральная симметричная продольная трещина в шве; д – трехточечный изгиб полосы с краевой трещиной; е – тавровый образец; ж- центральная симметричная поперечная трещина в шве
На основе численного эксперимента получены регрессионные зависимости для J-интеграла для образцов с краевой и центральной трещинами. Были рассмотрены семь типов материалов. С помощью программного пакета нетрадиционного математического моделирования многомерных зависимостей определены регрессионные зависимости и статистические характеристики для Jp-интеграла.
Работа выполнена при финансовой поддержке РФФИ в рамках гранта мол_ин_нр 13-08-90907.
Библиографическая ссылка
Терлецкая А.М., Даненова Г.Т., Лимарева И.Г., Сайлаукызы Ж.С. КОМПЛЕКСНАЯ МЕТОДИКА АВТОМАТИЗИРОВАННОГО АНАЛИЗА ЭЛЕМЕНТОВ ПРОСТРАНСТВЕННЫХ МЕХАНИЗМОВ С ИСПОЛЬЗОВАНИЕМ CAD/CAE-СИСТЕМ // Международный журнал прикладных и фундаментальных исследований. 2014. № 5-2. С. 36-40;URL: https://applied-research.ru/ru/article/view?id=5332 (дата обращения: 19.05.2025).