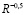Г. Галилей первым экспериментально установил универсальность ускорения свободного падения для Земли. И. Ньютону потребовалась Луна и математический анализ, чтобы установить закон Всемирного тяготения. Г. Леметр выдвинул гипотезу о том, что Вселенная представляет собой «черную дыру». Для обоснования гипотезы Г. Леметра потребовалось около ста лет, данные параметров всех планет Солнечной системы и развитая физическая теория: электромагнитная и квантовая. В результате получена Эмпирическая теория Вселенной (ЭТВ), которая не имеет признания научного сообщества [1-4]. С целью проверки выводов ЭТВ и в качестве практического приложения этой теории, выведем общие законы эволюции планет земной группы. Геологи не стали дожидаться создания фундаментальной физической теории и на основе наблюдательных данных своей науки развивают «Гипотезу расширяющейся Земли». Например, С.У. Кэри геологическую эволюцию Земли основывал на этой фундаментальной физической гипотезе расширения Вселенной.
Важным моментом в понимании ЭТВ является гипотеза о Вселенной как частице. Критерием существования такой частицы служит уравнение для «черной дыры», единое гравитационное поле (то есть пространство), единый световой поток и предопределенная структура материи. Поскольку скорость света больше скорости гравитона, то границы частицы под названием Вселенная определяются фронтом света вместе с которым «растягивается» пространство: 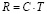 , где R – радиус Вселенной, C – скорость света, T – возраст Вселенной. Постоянство скорости носителя взаимодействия (фотона или гравитона) и независимость ее от системы отсчета приводит к важному свойству Вселенной: линейному росту линейных размеров и линейному росту массы составляющих ее тел. Структура Вселенной связана с конечной скоростью фотона и гравитона. Единственным «свободным» параметром такой Вселенной служит время (возраст Вселенной). В ЭТВ еще одна фундаментальная гравитационная константа GK (в дополнение к существующей гравитационной константе GN) связывает массу тела М с длиной волны его основного гравитона
, где R – радиус Вселенной, C – скорость света, T – возраст Вселенной. Постоянство скорости носителя взаимодействия (фотона или гравитона) и независимость ее от системы отсчета приводит к важному свойству Вселенной: линейному росту линейных размеров и линейному росту массы составляющих ее тел. Структура Вселенной связана с конечной скоростью фотона и гравитона. Единственным «свободным» параметром такой Вселенной служит время (возраст Вселенной). В ЭТВ еще одна фундаментальная гравитационная константа GK (в дополнение к существующей гравитационной константе GN) связывает массу тела М с длиной волны его основного гравитона 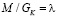 , то есть полностью определяет пространство вокруг тела (а не кривизну пространства, как в Общей теории относительности). «Большой взрыв» для описания такой Вселенной совсем не подходит, так же, как светимость и эволюция звезд должна быть увязана со свойствами Вселенной, а не с ядерными процессами в них. Понимание Вселенной как частицы позволяет разрешить спор о скорости гравитона. Вычисления по ЭТВ дают скорость гравитона, равную
, то есть полностью определяет пространство вокруг тела (а не кривизну пространства, как в Общей теории относительности). «Большой взрыв» для описания такой Вселенной совсем не подходит, так же, как светимость и эволюция звезд должна быть увязана со свойствами Вселенной, а не с ядерными процессами в них. Понимание Вселенной как частицы позволяет разрешить спор о скорости гравитона. Вычисления по ЭТВ дают скорость гравитона, равную 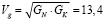 км/с. Однако гравитационное поле Солнца можно обнаружить в любой точке Вселенной, из чего следует не мгновенная скорость гравитона, а то, что поле Солнца там было всегда (как в любой частице), но в результате расширения Вселенной удалилось на очень большое расстояние от него.
км/с. Однако гравитационное поле Солнца можно обнаружить в любой точке Вселенной, из чего следует не мгновенная скорость гравитона, а то, что поле Солнца там было всегда (как в любой частице), но в результате расширения Вселенной удалилось на очень большое расстояние от него.
Для выведения общих законов эволюции планет использованы общие законы Вселенной, полученные в рамках ЭТВ и статистические (математические) методы обработки и представления данных. В нашем распоряжении имеется статистическое количество планет (Венера, Земля и Марс) для получения на их основе эмпирических законов эволюции, и планеты Меркурий и Луна для тестирования некоторых полученных законов. Исходными данными послужат астрономические и геофизические параметры планет земной группы [5, 6].
В данной статье рассмотрим классический метод оценки температур планет Солнечной системы. Предполагается, что источником тепла для всех этих планет служит излучение Солнца, а сами планеты не обладают собственными значимыми источниками тепла. То есть длительное время (миллиарды лет) температуры планет существенно не изменялись (равновесные температуры) и тепловой поток получаемый планетой от Солнца равен тепловому потоку излучаемому планетой.
Светимость космического тела (Солнце или планета) связана с его радиусом r и температурой T формулой Стефана – Больцмана:
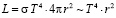 .
.
Поток солнечной радиации при среднем расстоянии от Солнца до планеты Ri равен
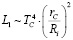 .
.
Здесь TC – температура в максимуме спектра и rC – радиус Солнца. Из этого потока на планету поступает количество энергии, равное произведению потока L1 на площадь поперечного сечения планеты 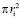 , то есть
, то есть
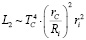 ,
,
где ri – средний радиус планеты. Планета, нагретая Солнечной радиацией до температуры Ti, в свою очередь излучает тепло всей поверхностью шара, равной 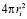 . Следовательно, устанавливается баланс тепловых потоков:
. Следовательно, устанавливается баланс тепловых потоков:
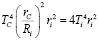 .
.
Тогда температура планеты равна
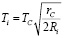
и не зависит от характеристик самой планеты, кроме радиуса орбиты. Поскольку температура TC и радиус rC Солнца в классической модели предполагаются постоянными, то температура планеты зависит от радиуса ее орбиты следующим образом (здесь Ti – температура в максимуме спектра теплового излучения планеты):
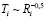 . (1)
. (1)
На основе данных о параметрах планет Солнечной системы проверим полученное соотношение. В табл. 1 приведены необходимые исходные данные: радиусы орбит планет и max / min наблюдаемые температуры. Такой выбор температур связан с условиями регистрации температур на планетах (наличие или отсутствие атмосферы, газовая среда или твердая поверхность), разными параметрами орбиты (эксцентриситет) и особенностями вращения планеты (скорость вращения, наклон оси). Предполагается, что полученный закон выполняется для всех планет независимо от других параметров кроме радиуса орбиты. В столбце 6 таблицы сразу вычислено значение R-0,5 для каждой планеты, а в столбцах 3 и 4 значения температур по двум регрессиям.
Радиус орбиты и температура (max и min) планеты
|
T max / min, K |
|
|
R, а.е. |
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
Венера |
800 / 735 |
319 |
396 |
1,082 |
0,961 |
|
Земля |
313 / 280 |
271 |
337 |
1,496 |
0,818 |
|
Марс |
290 / 170 |
220 |
273 |
2,279 |
0,662 |
|
Луна |
403 / 103 |
271 |
337 |
1,496 |
0,818 |
|
Меркурий |
700 / 90 |
436 |
542 |
0,579 |
1,314 |
|
Юпитер |
155 / 125 |
145 |
181 |
5,204 |
0,438 |
|
Сатурн |
134 / 85 |
107 |
133 |
9,582 |
0,323 |
|
Уран |
76 / 54 |
76 |
94 |
19,23 |
0,228 |
|
Нептун |
72 / 60 |
60 |
75 |
30,10 |
0,182 |
На рис. 1 построены диапазоны температур в зависимости от радиуса орбиты и по этим данным проведена степенная регрессионная зависимость. В результате показатель степени точно совпал с теоретическим показателем, и уравнение регрессии имеет вид: 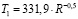 .
.
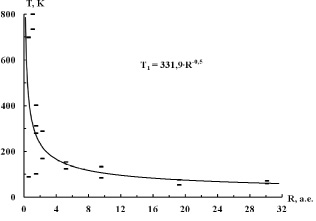
Рис. 1. Штрихи – диапазоны наблюдаемых температур на планетах, сплошная линия – степенная регрессионная зависимость 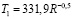 .
.
Из рис. 1 видно, что линия регрессии укладывается в диапазоны наблюдаемых температур планет за исключением Венеры и Земли (обладающих атмосферами и твердой поверхностью).
Человеческий глаз лучше воспринимает прямую линию (рис. 2). Для преобразования степенной функции в линейную зависимость используется стандартная процедура замены значений оси 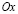 :
: 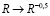 (то есть при построении графика вместо столбца 5 табл. 1 для оси х выбрать столбец 6). На рис. 2 помещена также предыдущая регрессия
(то есть при построении графика вместо столбца 5 табл. 1 для оси х выбрать столбец 6). На рис. 2 помещена также предыдущая регрессия 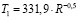 для сравнения (выделена серым цветом).
для сравнения (выделена серым цветом).
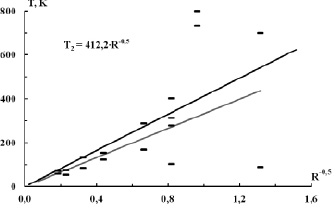
Рис. 2. Штрихи – диапазоны наблюдаемых температур на планетах, черная линия – регрессионная зависимость 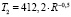 , полученная по исходным данным и серая линия – предыдущая эмпирическая зависимость T1.
, полученная по исходным данным и серая линия – предыдущая эмпирическая зависимость T1.
Из рис. 2 видно, что зависимость T1 достаточно точно проходит по серединам диапазонов наблюдаемых температур. Новая зависимость получена при условии прохождения через начало координат (что не совсем правильно). Зависимость T2 явно тяготеет к верхним значениям диапазонов температур, что связано с использованием метода наименьших квадратов при получении регрессий в условиях большого разброса исходных данных. Рассматриваемый пример отягощен еще одной проблемой. При получении зависимости T1 большой диапазон температур Меркурия и выпадающие значения для Венеры попали на малые значения R, в результате чего не оказали существенного влияния на качество регрессии. При получении зависимости T2 выпадающие значения температур Венеры приходятся на большие значения R-0,5, что привело к существенному завышению значений температур. При исключении Венеры из исходных данных зависимость T2 практически совпадает с T1.
Воспользуемся методами линеаризации функций и преобразуем степенную функцию 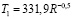 к линейному виду иным способом. Для этого по оси Oy отложим величину TR0,5 и по оси Ox – R. Если по модифицированным данным снова провести степенную регрессию (но не линейную), то новая зависимость должна представлять собой горизонтальную прямую на уровне 331,9 (рис. 3).
к линейному виду иным способом. Для этого по оси Oy отложим величину TR0,5 и по оси Ox – R. Если по модифицированным данным снова провести степенную регрессию (но не линейную), то новая зависимость должна представлять собой горизонтальную прямую на уровне 331,9 (рис. 3).
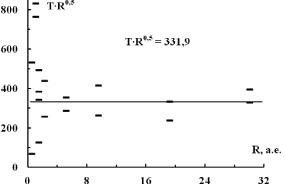
Рис. 3. Штрихи – диапазоны исходных модифицированных данных 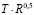 , линия – степенная регрессия по ним
, линия – степенная регрессия по ним
Проведенный анализ температур планет полностью подтвердил классический закон передачи тепла от Солнца планетам. Вместе с тем имеются методические разногласия в измерении температуры на планетах в силу объективных причин их устройства. Например, в качестве температуры планет земной группы использовались температуры, измеренные на их поверхности. Наличие атмосферы у Венеры, Земли и Марса существенно искажает результат, что хорошо видно на рисунке 3. Отсутствие атмосферы у Луны и Меркурия малая скорость их вращения приводит к очень большому разбросу температур. На планетах-гигантах температура измеряется в газовом слое, данные в статье приведены для слоя при давлении 1 Бар (общепринятый критерий). При этом температура в уравнении (1) соответствует температуре в максимуме спектра теплового излучения планеты. Из всех анализируемых температур планет критерию уравнения (1) как раз не соответствуют температуры Венеры, Земли и Марса.
Для выяснения геологической, химической и биологической эволюции планет земной группы необходимы именно температуры их поверхности, которые сильно зависят от величины (давления) атмосферы. Кроме того, здесь анализировались современные температуры, а для указанных целей необходимо знать эволюцию температур за миллиарды лет [7]. Простые законы эволюции Вселенной: линейный рост линейных размеров и линейный рост массы всех тел помогут разрешить проблему. В [8], на основе Эмпирической Теории Вселенной, приведена оценка возраста Солнечной системы (T = 10.1 млрд. лет), скорость удаления Земли от Солнца (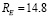 метров в год), скорость увеличения радиуса Земли (
метров в год), скорость увеличения радиуса Земли (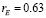 миллиметра в год) и простые соотношения для вычисления изменения параметров любой планеты.
миллиметра в год) и простые соотношения для вычисления изменения параметров любой планеты.
Библиографическая ссылка
Курков А.А. ЗАКОНЫ ЭВОЛЮЦИИ ПЛАНЕТ: ТЕМПЕРАТУРА КЛАССИЧЕСКИЕ ЗАКОНОМЕРНОСТИ // Международный журнал прикладных и фундаментальных исследований. 2014. № 5-2. С. 125-129;URL: https://applied-research.ru/ru/article/view?id=5352 (дата обращения: 03.03.2026).


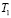 , K
, K
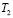 , K
, K