Функционирование любой сложной системы, включая экономические (ЭС), целесообразно описывать с использованием системно-аналитического подхода, который предполагает не только наличие исследовательской концепции, содержательных и математических моделей, но и возможность проведения их эффективного численного анализа, позволяющих решать практически значимые задачи и разрабатывать автоматизированные средства поддержки принятия решений при управлении ЭС.
Одним из эффективных инструментов изучения динамических систем, отвечающих указанным системно-аналитическим требованиям, является многокритериальная, многошаговая задача линейного программирования (управления) ММЗЛП:
x(t + 1) = A(t)x(t) + B(t)u(t); x(t) = a;
C(t)x(t) + D(t)u(t) ≤ h(t); u(t) ≥ 0 (t = 0,…,T–1);
,
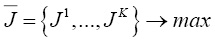где u(t) = [ul(t)] и x(t) = [xi(t)] – соответственно управляющий и фазовый векторы; матрицы A(t) = [aij(t)]; B(t) = [bil(t)]; C(t) = [ckj(t)]; D(t) = [dik(t)]; векторы a(t) = [ai(t)]; b(t) = [bl(t)]; s(t) = [si(t)]; h(t) = [hk(t)]; (i,j = 1,…,n; l = 1,…,r; k = 1,…,m; t = 0,…,T);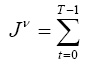 
[av(t), x(t)) +
(bv(t), u(t))] + av(T), xv(T)) – ν-тый целевой критерий (ν = 1,…,K); K – количество критериев; r, m, T – размерность управляющего вектора, число ограничений и временных шагов соответственно; (α0, β0) – скалярное произведение векторов α0, β0.
Предположим, что задача (1) описывает развитие некоторой ЭС. При большом количестве шагов (горизонте планирования) Т в ЭС справедлив закон временной
стоимости денежных потоков, который для (1) может быть смоделирован применением операции дисконтирования коэффициентов целевых критериев:
.
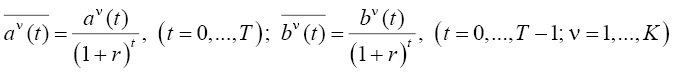При математическом моделировании стратегического развития ЭС возникает ряд принципиальных вопросов: 1) какие минимально необходимые группы содержательных переменных целесообразно включить в вектора u(t) и x(t) для отражения основных потребностей аналитиков при прогнозировании стратегического развития ЭС; 2) каков минимально необходимый набор содержательных ограничений, которым подвергается функционирование ЭС. Ответ на первый вопрос, очевидно, определяет размерности n, r управляющего, фазового вектора и матриц в уравнениях динамики, а на второй – размерности матриц в ограничениях-неравенствах задачи (1). Кроме того, учитывая, что ЭС является сложной системой, ее изучение без учета интересов нескольких участников будет ограничивать практическую значимость результатов исследования. Последнее порождает еще один принципиальный вопрос о минимально целесообразном значении параметра K (количество критериев в ММЗЛП).
Будем исходить из, вообще говоря, аксиоматического положения о том, что функционирование ЭС невозможно без производителя (Р), порождающего «основу ее существования» путем производства заданного количества товаров и услуг. В своей деятельности (Р) мотивирован и ограничен существенными интересами, как правило, еще двух участников ЭС – потребителя (С) и управляющего (налогового) органа (Т), что позволяет выдвинуть гипотезу о целесообразном для анализа ЭС значении K = 1,2,3. Отметим, что данный вывод не исключает построения ЭС с большим значением К, с учетом функционирования, например, коммерческого (Сom), финансового (F) и других институциональных посредников. Вместе с тем, указанные посредники могут трактоваться и как составляющие (Р), производящие соответствующие услуги: (Com) – по доставке произведенного (Р) товара для (С), а (F) – по аккумулированию временно свободных финансовых ресурсов (Р), (С), (Com) и (T) с целью последующего предоставления их, например, в виде инвестиционных кредитов.
Предположим, что структурно неоднородный экономический агент (Р) представлен производственной фирмой, деятельность которой делится на три составляющие – инвестиционную, производственную и финансовую [1]. В соответствии с этим разделим переменные и ограничения ММЗЛП (1) на инвестиционные, производственные и финансовые. В таблице отражена информация о взаимодействии ограничений и переменных в математических моделях ЭС, многочисленные реализации которых описаны в работах [2, 3].
Матрица «ограничения-переменные» для математической модели ЭС
|
Ограничения |
Переменные |
|||||
|
Инвестиционные (И) |
Производственные (П) |
Финансовые (Ф) |
||||
|
Управляющие (УИ) |
Фазовые (ФИ) |
Управляющие (УП) |
Фазовые (ФП) |
Управляющие (УФ) |
Фазовые (ФФ) |
|
|
Инвестиционные (ОИ) |
|
|
|
|
|
|
|
Производственные (ОП) |
|
|
|
|
|
|
|
Финансовые (ОФ) |
|
|
|
|
|
|
Тонированные клетки в таблице указывают, какие переменные задействуются в соответствующих ограничениях математических моделей. Переменные имеют следующий содержательный смысл. УИ – инвестиции в текущий момент времени на приобретение комплекта основных производственных фондов (ОПФ), ФИ – накопленные инвестиции в ОПФ; УП – стоимость в текущий момент времени реализуемой продукции, ФП – накопленные амортизационные отчисления, стоимость реализованной продукции; УФ и ФФ – стоимостное выражение (соответственно, в текущий момент и накопленных) потоков кредитов, депозитов, дотаций и других финансовых инструментов. Ограничения, описывающие функционирование ЭС, имеют следующий содержательный смысл. Уравнения: динамика фазовых переменных ФИ, ФП, ФФ. Неравенства: ОИ – по суммарному объему инвестиций, ОП – по фондоотдаче ОПФ и по спросу на продукцию, ОФ – по суммарному объему финансовых инструментов.
Следует отметить, что использование переменных таблицы позволяет строить критериальные функционалы качества в форме производственных функций, алгоритмически соответствующих бухгалтерским правилам учета доходов и затрат, что благосклонно воспринимается финансовыми аналитиками и отличает данный подход от часто используемого исследователями построения производственных функций на основе функций типа Кобба-Дугласа и других идеализированных функционалов качества. Использование указанных в таблице переменных позволяет:
● рассчитывать основные показатели финансово-хозяйственной деятельности фирмы: потоки прибыли, амортизации, оплаты труда, кредитов, штрафов, основные виды налогов и сборов и т.п.;
● описывать ограничения функционирования ЭС, связанные с производственными, инвестиционными и финансовыми возможностями ЭС: платежеспособность (P), (C), (T) и других участников ЭС, ограниченность выпуска спросом на продукцию и возможностями ОПФ, кредитно-депозитные, страховые, дотационные и т.п. ограничения.
Отметим, что алгоритмы расчета показателей финансово-хозяйственной деятельности фирмы корректно описываются линейными функциями от указанных в таблице переменных, что, на наш взгляд, является важным аргументом в пользу использования задачи (1) для реализации системно-аналитической концепции изучения ЭС.
В работе [2], в частности, обоснована возможность математически корректного превращения задачи (1), путем применения к векторам x(t) и u(t) (доопределенным нулевыми компонентами на бесконечном горизонте планирования) z-оператора:
,
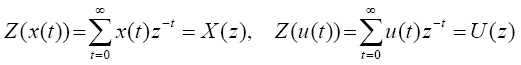(здесь z = 1+r)
в статическую, z-параметрическую задачу линейного программирования, сохраняющую основные качественные свойства исходной (оптимальные пропорции инвестиций, выпусков продукции, структуру, параметрические зависимости Парето-множеств и т.п.). Помимо указанного преимущества, применение операционного метода позволяет значительно упростить процедуру доказательства существования решения исходной динамической задачи. Полученная статическая задача допускает эффективный численный анализ и может быть решена для практически значимых размерностей, определяемых в ЭС, прежде всего, количеством видов производимой продукции.
Описанный выше подход к моделированию ЭС, в части классификации переменных и ограничений, применения операционного метода и других элементов концепции, позволил построить и проанализировать многочисленные модели ЭС в форме ММЗЛП (см. обзор [4]), а также добиться их эффективной численной реализации с выходом на поддержку принятия решений, опирающихся на программные системы [5].
Полученный опыт системного анализа ЭС позволил параллельно разработать подход, связанный с непосредственным конструированием и анализом многокритериальных одношаговых задач линейного программирования (МОЗЛП). При использовании данного подхода принципиально сохраняется классификация переменных и ограничений таблицы, но модифицируется их структура (устраняется деление переменных на фазовые и управляющие) и содержательная трактовка. А именно, инвестиционные переменные трактуются как суммарная стоимость ОПФ (суммарные инвестиции), а производственные переменные – как суммарная стоимость произведенной продукции на всем горизонте планирования. Основанный на
использовании МОЗЛП подход позволил построить и проанализировать (см. обзор [6]) математические модели ЭС в форме многопараметрических ЗЛП практически значимых размерностей. В работе [7] предложена модель регионального развития в форме МОЗЛП, наиболее полно реализующая классификацию переменных и ограничений таблицы. Численная реализация МОЗЛП на основе симплекс-метода дала возможность выйти на разработку полноценных систем поддержки принятия решений, позволивших решить различные задачи анализа реальных ЭС микро- и мезоуровня, инвестиционных проектов и финансово-хозяйственной деятельности предприятий, что подтверждается актами об апробации и использовании программных систем и другими приложениями разработанного системно-аналитического подхода, включающего всю цепочку от математических моделей и методов их анализа до автоматизированных программных продуктов [5] и систем поддержки принятия решений [8], ориентированных на конечного пользователя – предпринимателя, бизнесмена, финансового аналитика.
Библиографическая ссылка
Медведев А.В. ОБ ЭФФЕКТИВНОМ ИНСТРУМЕНТАРИИ АНАЛИЗА ЭКОНОМИЧЕСКИХ СИСТЕМ // Международный журнал прикладных и фундаментальных исследований. 2014. № 11-5. С. 763-766;URL: https://applied-research.ru/ru/article/view?id=6222 (дата обращения: 03.04.2025).