Изучение задач, связанных с движением вязкой жидкости в различных гидромеханических условиях, осуществляется на протяжении длительного времени с неизменным сохранением актуальности [1–3]. В частности, выполняются исследования, направленные на выявление эффектов среднего движения жидкости, подвергающейся периодическим по времени (колебательным, вибрационным) воздействиям ([4, 5] и представленная в этих источниках литература). В настоящей работе поставлена и решена новая задача о движении вязкой жидкости, обусловленной колебательными воздействиями на жидкость, характеризующимися отсутствием выделенного направления в пространстве. Жидкость контактирует с абсолютно твердыми стенками W1, W2 и пластиной Ξ. Стенки совершают заданные колебания вдоль оси Y инерциальной прямоугольной системы координат X, Y, Z. Стенка W1 ограничена плоскостью Y = A1, стенка W2 – плоскостью Y = A2. Толщина пластины пренебрежимо мала (равна нулю); пластина находится в плоскости Y = B (A1 < B < A2; B – постоянная). Промежутки между стенками и пластиной – области Ω1 : A1 < Y < B и Ω2 : B < Y < A2 (–∞ < X < ∞, –∞ < Z < ∞) – заполнены жидкостью. Расстояние между стенками L = A2 – A1 постоянно. Пластина проницаема для жидкости; пластина движется вдоль оси X под действием внешних колебательных сил и сил со стороны жидкости.
Целью работы является определение не зависящего от начальных данных периодического по времени t движения жидкости.
Постановка и решение задачи
Пусть T – период колебаний стенок W1, W2; τ = t / T; x = X / L; y = Y / L; z = Z / L; 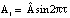 (
(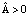 – постоянная);
– постоянная); 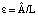 ; a1 = A1 / L; a2 = A2 / L; b = B/L; ξ – часть пластины Ξ длиной DX, «вписанная» между плоскостями Z = Z* и Z = Z* + DZ (Z*, DX > 0, DZ > 0 – постоянные); m – масса тела ξ;
; a1 = A1 / L; a2 = A2 / L; b = B/L; ξ – часть пластины Ξ длиной DX, «вписанная» между плоскостями Z = Z* и Z = Z* + DZ (Z*, DX > 0, DZ > 0 – постоянные); m – масса тела ξ; 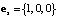
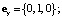
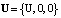 – скорость тела ξ (пластины Ξ); u = TU / L; ρ, ν, V = {VX, VY, 0} – соответственно плотность, кинематический коэффициент вязкости и скорость жидкости; v = TV/L (v = {vx, vy, 0} = v(y, τ)); P – давление в жидкости;
– скорость тела ξ (пластины Ξ); u = TU / L; ρ, ν, V = {VX, VY, 0} – соответственно плотность, кинематический коэффициент вязкости и скорость жидкости; v = TV/L (v = {vx, vy, 0} = v(y, τ)); P – давление в жидкости; 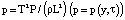 ;
; 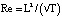 – число Рейнольдса;
– число Рейнольдса; 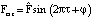 – внешняя сила, действующая на тело ξ в направлении оси X (
– внешняя сила, действующая на тело ξ в направлении оси X ( , φ – постоянные);
, φ – постоянные); 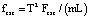 ;
; 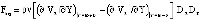 – сила, действующая со стороны жидкости на тело ξ в направлении оси X;
– сила, действующая со стороны жидкости на тело ξ в направлении оси X; 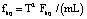 .
.
Постановка задачи включает в себя уравнение движения тела ξ (пластины Ξ), уравнения Навье – Стокса и неразрывности и условия, которые должны выполняться на границах тел W1, W2, Ξ:
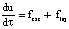 ; (1)
; (1)
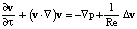 в Ω1, Ω2; (2)
в Ω1, Ω2; (2)
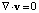 в Ω1, Ω2; (3)
в Ω1, Ω2; (3)
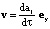 при
при 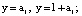 (4)
(4)
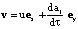 при
при 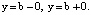 (5)
(5)
Из (3)–(5) следует
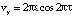 при
при 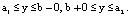 (6)
(6)
Согласно (2), (4)–(6) имеем
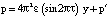 при a1 < y < b,
при a1 < y < b,
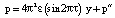 при b < y < a2 (7)
при b < y < a2 (7)
(p', p" – функции τ);
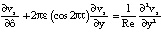 в Ω1, Ω2; (8)
в Ω1, Ω2; (8)
vx = 0 при y = a1, y = 1 + a1; (9)
vx = u при y = b – 0, y = b + 0. (10)
Будем рассматривать задачу (1), (8)–(10) при малых по сравнению с единицей значениях ε.
Предположим, что
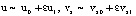 при ε → 0. (11)
при ε → 0. (11)
Пусть N = 0, 1 – номер приближения (степень ε).
Используя (1), (8)–(11), получим
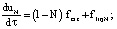 (12)
(12)
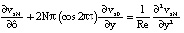 в
в 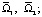 (13)
(13)
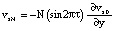 при y = 0, y = 1; (14)
при y = 0, y = 1; (14)
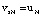 при y = b – 0, y = b + 0. (15)
при y = b – 0, y = b + 0. (15)
Здесь 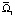 и
и 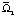 – области соответственно 0 < y < b и b < y < 1
– области соответственно 0 < y < b и b < y < 1
(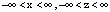 );
);
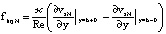
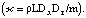
Пусть N = 0.
Задача (12)–(15) имеет решение
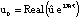 (16)
(16)
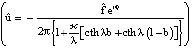 ;
;
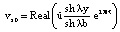 при
при 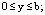 (17)
(17)
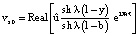 при
при 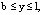 (18)
(18)
где 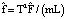 ;
; 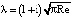 .
.
Пусть N = 1.
Из (12)–(15) следует
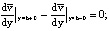 (19)
(19)
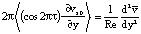 в
в 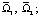 (20)
(20)
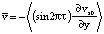 при
при 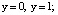 (21)
(21)
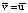 при
при 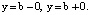 (22)
(22)
Здесь 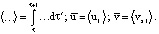
Задача (12)–(15) имеет решение
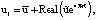
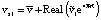 при
при 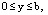
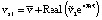 при
при 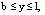 (23)
(23)
где 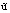 – постоянная;
– постоянная; 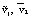 – функции y.
– функции y.
Используя (16)–(22), найдем
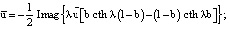 (24)
(24)
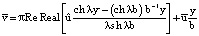 при
при 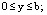 (25)
(25)
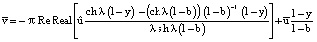 при
при 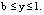 (26)
(26)
Формулами
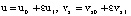 (27)
(27)
и (6), (7), (16)–(18), (23)–(26) определяется приближенное решение задачи (1)–(5). Из этого решения, в частности, следует, что жидкость (на фоне колебаний) совершает стационарное, прямолинейное движение. Отметим, что при b = 1/2 пластина Ξ (на фоне колебаний) неподвижна.
Остановимся на вопросе о среднем по времени движении жидкости при малых по сравнению с единицей значениях Re.
Используя (6), (16)–(18), (23)–(27), получим
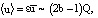
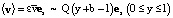 при
при 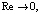 (28)
(28)
где 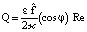 .
.
Согласно (28) (на фоне колебаний, для Q ≠ 0) имеет место следующее. При b > 1/2 (b < 1) в области 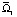 присутствуют два слоя, определяемые соотношениями 0 < y < 1 – b (слой l1) и 1 – b < y < b, в которых жидкость движется во взаимно противоположных направлениях, причем направление движения жидкости в слое l1 противоположно направлению движения пластины Ξ; в области
присутствуют два слоя, определяемые соотношениями 0 < y < 1 – b (слой l1) и 1 – b < y < b, в которых жидкость движется во взаимно противоположных направлениях, причем направление движения жидкости в слое l1 противоположно направлению движения пластины Ξ; в области 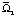 (в слое b < y < 1) жидкость движется в одном направлении, которое совпадает с направлением движения пластины Ξ. Отметим, что толщина слоя l1 равна «толщине» области
(в слое b < y < 1) жидкость движется в одном направлении, которое совпадает с направлением движения пластины Ξ. Отметим, что толщина слоя l1 равна «толщине» области 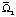 . При b < 1/2 (b > 0 в области
. При b < 1/2 (b > 0 в области 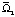 присутствуют два слоя, определяемые соотношениями b < y < 1 – b и 1 – b < y < 1 (слой l2), в которых жидкость движется во взаимно противоположных направлениях, причем направление движения жидкости в слое l2 противоположно направлению движения пластины Ξ; в области
присутствуют два слоя, определяемые соотношениями b < y < 1 – b и 1 – b < y < 1 (слой l2), в которых жидкость движется во взаимно противоположных направлениях, причем направление движения жидкости в слое l2 противоположно направлению движения пластины Ξ; в области 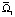 (в слое 0 < y < b) жидкость движется в одном направлении, которое совпадает с направлением движения пластины Ξ. Отметим, что толщина слоя l2 равна «толщине» области
(в слое 0 < y < b) жидкость движется в одном направлении, которое совпадает с направлением движения пластины Ξ. Отметим, что толщина слоя l2 равна «толщине» области 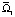 . При b = 1/2 пластина Ξ неподвижна; жидкость в каждой из областей
. При b = 1/2 пластина Ξ неподвижна; жидкость в каждой из областей 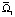 ,
, 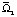 движется в одном направлении, и эти направления взаимно противоположны.
движется в одном направлении, и эти направления взаимно противоположны.
Отметим, что (при Q ≠ 0) среднее по времени движение жидких слоев происходит при любом положении пластины между стенками.
Заключение
Представленное в настоящей работе свидетельствует о том, что жидкость в рассмотренных условиях совершает движение в выделенном направлении, вызываемое и поддерживаемое оказываемыми на жидкость воздействиями, не имеющими выделенного направления в пространстве. Происходит «порождение порядка из хаоса». Причина данного эффекта состоит в согласованности (друг с другом) оказываемых на жидкость воздействий, что находится в непосредственной связи с принципом среднего движения [6], который в обобщенном виде может быть сформулирован следующим образом.
Основополагающей причиной среднего по времени движения свободных частей гидромеханической системы (частей системы, движение которых не задано) при периодических по времени (колебательных, вибрационных) воздействиях на систему, не имеющих выделенного направления в пространстве, является возможность совершения свободными частями системы движения в различных направлениях в пространстве в неодинаковых условиях.
Результаты, полученные в настоящей работе, в частности, могут служить теоретической основой для проведения направленных экспериментальных исследований движения жидкости в рассмотренных и аналогичных им гидромеханических условиях.

