Общая постановка и вариационый подход решения нестационарной задачи распространения тепла в стержне при воздействии теплового потока и в условиях теплообмена рассмотрены в [1]. Согласно этому подходу определяется аппроксимация температур T и вычисляется выражение
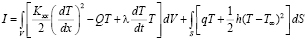, (1)
где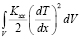 
– часть тепла, которая уходит на повышение внутренней энергии; 
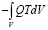– внутренние источники энергии; 
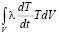– член, учитывающий нестационарность задачи; 
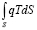– количество поступающего тепла; 
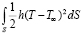– количества тепла, уходящего через поверхность стержня.
Здесь введены следующие обозначения:
q – тепловой поток (Bт/см2);
T – температура (0С);
S – площадь поперечного сечения стержня (см2);
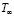– температура окружающей среды (÷С);
λ=ρc – коэффициент температуропроводности (Bт/(см2•0С));
h – коэффициент теплоотдачи (Bт/(см2•λ=ρcС));
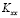– коэффициент теплопроводности материала (Bт/(см•0С));
Q – источник тепла внутри тела (Bт/(см•0С));
ρ – плотность (кг/см2);
c – удельная теплоемкость (Bт/(кг•0С)).
При линейной аппроксимации температуры T стержня длиной L с температурами на концах (Т1, Т2) имеем
.
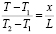Откуда
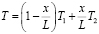. (2)
Первое выражение (1) для стержня длиной 2L с температурами на концах (Т1, Т2) и в середине Т2 имеет вид
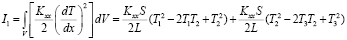. (3)
Выражение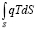 
для левого конца стержня:
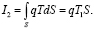(4)
Поток тепла на правом конце стержня равен
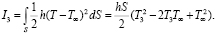(5)
Так как боковая поверхность стержня не теплоизолирована, вычислим член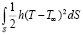 
для двух интервалов:
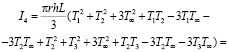
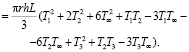(6)
В нестационарном случае, подставляя производную T по t из (2) в соотношение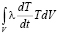 
, получим
+
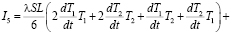
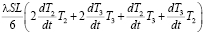. (7)
Тогда выражение (1) можно записать в виде
.
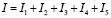Определяя производные от I по T1, T2 и Т3 и приравнивая к нулю, получим систему дифференциальных уравнений:
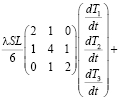
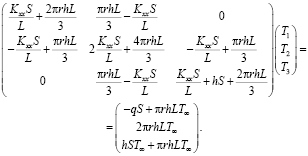(8)
Рассмотрим теперь метод взвешенных невязок, а точнее, метод Галеркина.
Общее уравнение теплопроводности стержня имеет вид
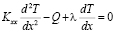, (9)
при ограничениях
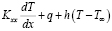=0. (10)
Решим уравнение (9) при ограничениях (10) методом Галеркина с использованием линейной аппроксимации температуры на двух интервалах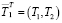 
и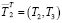 
. Для первого интервала имеем
, 
=
, 
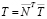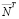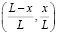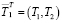. (11)
Согласно методу Галеркина [2] решение задачи (9) при ограничениях (10) должно удовлетворять уравнению:
– 
+
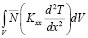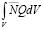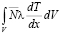=0. (12)
Первый интеграл преобразуем следующим образом:
=
–
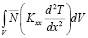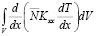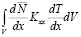. (13)
Вычислим второй интеграл выражения (13):
=
=
=
=
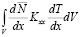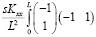
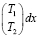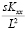
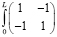
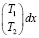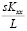
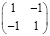
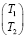. (14)
Вычислим первый интеграл выражения (13) с использованием формулы Остроградского-Гаусса. Имеем
=
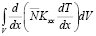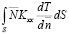, (15)
где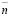 
– нормаль к поверхности.
Уравнение (15) для левого конца стержня, исходя из граничного условия
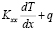=0, (16)
имеет вид
=
=
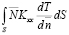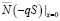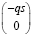. (17)
А на правом конце стержня, учитывая граничное условие
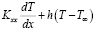=0, (18)
имеем
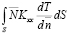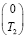=–hs
+hs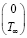
. (19)
Если тепло уходит через боковую поверхность, то граничное условие (18) имеет вид
.
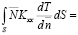
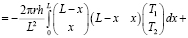
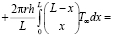
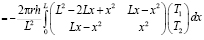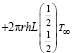
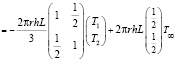. (20)
Вычислим третий член в уравнении (12).
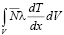
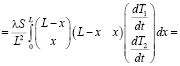
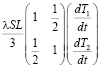. (21)
Формулы (14), (17), (19)–(21) позволяют получить следующую систему обыкновенных дифференциальных уравнений:
+
–
+
+
– 
+
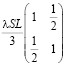
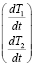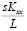
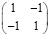
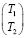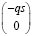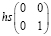
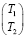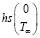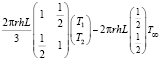=0. (22)
Уравнение (14) можно преобразовать к виду
.
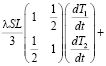
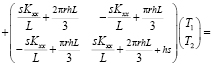
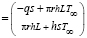Если возьмем два интервала, то для первого имеем
,
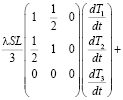
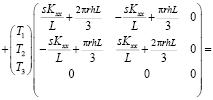
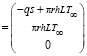а для второго интервала:
.
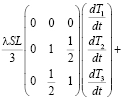
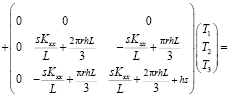
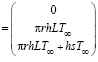Объединяя эти две системы линейных дифференциальных уравнений, получим (8).
Таким образом, вариационный подход и метод Галеркина при решении нестационарной задачи распространения тепла в стержне приводят к одинаковым системам дифференциальных уравнений и, следовательно, к одинаковым решениям.