Одним из вариантов выведения спутника на околоземную орбиту является горизонтальный старт, при котором ракета отделяется от самолета-носителя на некоторой высоте с дозвуковой скоростью, после чего происходит включение двигателей непосредственно самой ракеты. За счет этого возможно уменьшение стартовой массы ракеты-носителя и удешевление вывода на низкую околоземную орбиту небольших по размеру спутников. В работе [1] проводился численный эксперимент по оптимизации управления вектором тяги при упрощенной модели аэродинамического сопротивления: предполагался постоянным коэффициент аэродинамического сопротивления. Проведенные в настоящей работе расчеты отличаются уточненной моделью аэродинамического сопротивления. Предполагалось наличие аэродинамических рулей, позволяющих поддерживать нулевым угол атаки ракеты. Задача оптимизации управления вектором тяги была решена методом пристрелки с использованием принципа максимума Понтрягина. Расчет аэродинамического сопротивления проводился по формуле
,
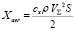где сх – коэффициент аэродинамического сопротивления, ρ – плотность воздуха, зависящая от высоты,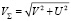 
– скорость полета, V – составляющая скорости, перпендикулярной радиусу Земли, U – составляющая скорости вдоль радиуса, S – характерная площадь летательного аппарата (в данной задаче площадь миделя ракеты). Зависимость сх = f(M) представлена в [2].
M = VΣ / a,
где M – число Маха полета,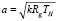 
– скорость звука на заданной высоте, k = 1,4 – показатель адиабаты для воздуха, Rg – газовая постоянная для воздуха, TH – температура воздуха на заданной высоте в градусах Кельвина в соответствии с МСА. Изменение плотности воздуха и скорости звука по высоте моделируется в соответствии с [3].
Цель исследования – изменив алгоритм расчета аэродинамического сопротивления с учетом данных МСА и зависимости сх = f(M), решить задачу оптимизации управления углом действия вектора тяги, а также проанализировать полученные результаты в сравнении с данными [1].
Математические модели и численные методы
Метод оптимизации – принцип максимума Понтрягина, численный метод решения краевой задачи – метод пристрелки.
Критерий эффективности управления – минимум затрат топлива на выполнение миссии, что соответствует минимуму времени вывода ракеты на орбиту при постоянном расходе топлива. Функционал задачи оптимального управления имеет вид
.
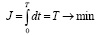Система уравнений движения в геоцентрической полярной системе координат:
,
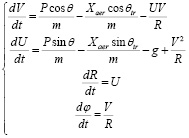где R – радиус ракеты при начале координат в центре Земли, м; V – тангенциальная скорость ракеты, м/с; U – радиальная скорость, м/с; φ– полярный угол, рад; P = JGT – тяга двигателя, Н; J – импульс ракетного двигателя, м/с; GT – расход топлива, кг/с; Xaer – сила аэродинамического сопротивления, Н; m – масса ракеты, кг;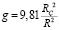 
– ускорение свободного падения, м/с2, RЗ – радиус Земли, м; t – время, с, θ – управление, угол действия тяги (между осью ракеты и вектором тяги), рад, θrt – траекторный угол (между скоростью и перпендикуляром к местному радиусу), рад,
;
;
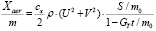где S / m0 – площадь миделя ракеты, деленная на стартовую массу.
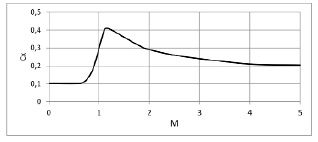
Рис. 1. Зависимость коэффициента аэродинамического сопротивления от числа Маха полета при нулевом угле атаки
Функция Понтрягина имеет вид
,
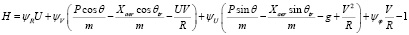где ψR , ψV , ψU , ψφ – сопряженные переменные. Здесь следует отметить, что в функции Понтрягина необходимо учитывать постоянную величину интегранта (единицу, стоящую под интегралом в выражении функционала), так как при решении методом пристрелки будет невязка по функции Понтрягина в конечный момент времени.
Оптимальное управление вектором тяги в соответствии с принципом максимума Понтрягина можно определить по максимуму функции Понтрягина при нелинейности ее по управлению из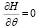 
.
Продифференцировав функцию Понтрягина по управлению, получим для оптимального управления: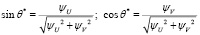 
.
Сопряженная система, соответствующая исходной системе уравнений движения:
.
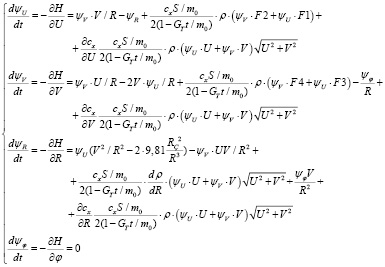
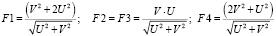При условии зависимости коэффициента аэродинамического сопротивления от Маха полета, а следовательно, от тангенциальной и радиальной скорости, а также от температуры атмосферного воздуха и, соответственно, от высоты (радиуса) полета, необходимо получить частные производные сх по этим переменным:
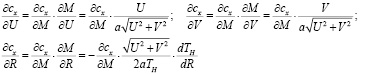
Следует отметить, что производные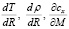 
получены численным методом с использованием линейной интерполяции табличных данных МСА и кривой аэродинамического сопротивления, что приводит к разрывам производных в точках табличных значений. Таким образом, помимо поставленной задачи проводилось исследование на возможность использования линейной интерполяции некоторых переменных при использовании метода численного решения системы нелинейных алгебраических уравнений – метода Ньютона (используется как составная часть в методе пристрелки). Подобные действия не рекомендованы при использовании численных методов, основанных на линеаризации систем алгебраических уравнений и вычислении производных функций-невязок. Несмотря на это, удалось реализовать численный метод решения краевой задачи и добиться сходимости метода пристрелки.
Старт ракеты с самолета-носителя принимался на высоте 13000 м и горизонтальной скорости полета, соответствующей числу Маха М = 0,85. Радиальная составляющая скорости задавалась равной нулю. Удельный импульс двигателя принимался равным 2000 м/с.
Дополнив систему уравнений движения сопряженной системой, получим П-систему, которая представляет собой систему обыкновенных дифференциальных уравнений с краевыми условиями. Краевые условия:
R(0) = 6384000 м, R(T) = 6471000 м,
U(0) = U(T) = 0,
V(0) = 236,11 м/сек, φ(0) = 0,
V(T) = 7844,3 м/сек, ψφ(T) = 0.
Равенство нулю ψφ(T) вытекает из условий трансверсальности задачи оптимального управления. Методы решения задач оптимального управления рассмотрены в [4, 5]. В данной работе использовался метод пристрелки. Метод пристрелки или стрельбы дает наиболее точные результаты численного решения краевых задач [4]. Возможность решения реальных задач оптимального управления указанным методом, как для задач без ограничений по управлению, так и для задач с переключением управления, показана в [6, 7]. Метод пристрелки использует в качестве внешнего цикла модифицированный метод Ньютона, в качестве внутреннего, к которому обращается метод Ньютона, – численный метод решения систем обыкновенных дифференциальных уравнений: метод Рунге – Кутты 4-го порядка. Для более точного выхода из метода Рунге – Кутты был введен новый аргумент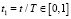 
, где Т – неизвестное время вывода ракеты на орбиту. П-система получает изменения, связанные с ведением этого нового аргумента.
Параметры пристрелки для этого варианта расчета выбирались следующие:
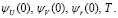
Им соответствуют невязки:
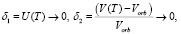
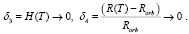
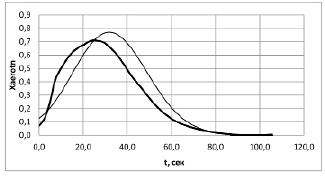
Рис. 2. Значение относительных значений аэродинамического сопротивления при различных моделях определения сх
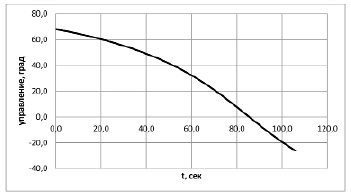
Рис. 3. Оптимальный угол действия тяги двигателя (угол между осью летательного аппарата и вектором тяги)
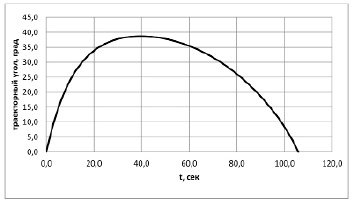
Рис. 4. Траекторный угол при оптимальном управлении
Выход из метода Ньютона осуществлялся по условию: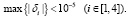 
Результаты расчетов
На рис. 2 приведены относительные значения аэродинамического сопротивления, полученные в расчете с постоянным коэффициентом аэродинамического сопротивления (тонкая линия) и с уточненным значением, зависящим от числа Маха полета (толстая линия).
Относительная величина аэродинамического ускорения есть не что иное, как ускорение от сопротивления атмосферного воздуха. На рис. 3 и 4 приведены значения оптимального угла действия тяги и траекторного угла. Кривые на рис. 3 и 4 для проведенного расчета и выполненного в [1] практически совпадают. Это объясняется тем, что сила тяги превышает сопротивление воздуха более чем в 30 раз.
Заключение
Показано, что использование уточненной модели аэродинамического сопротивления при рассматриваемой постановке задачи не дает существенного изменения результатов оптимизации управления вектором тяги. При решении подобных задач вертикального старта результат может качественно измениться.
Полученные результаты по изменению величины аэродинамического сопротивления могут представлять интерес, например, для задач по исследованию нагрева носовой части ракеты, что не рассматривалось в данной работе. Следует отметить, что в математической модели не были учтены конструкторские ограничения, такие как допустимые углы поворота вектора тяги и прочностные ограничения.
Линейная интерполяция коэффициента аэродинамического сопротивления и температуры воздуха по высоте не повлияла на сходимость метода Ньютона, хотя и связана с возникновением разрывов производных этих величин.