Введение
В динамике твердого тела для изучения свойств движения применяются различные методы и параметры (метод инвариантных соотношений (ИС)[10], углы Эйлера [1-4], параметры Родрига-Гамильтона (Р.-Г.)[5-7,11] и другие). На их базе получена значительная информация о движении твердого тела под действием силы тяжести [2,3] и под действием потенциальных и гироскопических сил [4]. Использование параметров Р.-Г. актуально не только в задачах ориентации движущихся объектов [7,11], но и при изучении колебаний тяжелого твердого тела с неподвижной точкой [5]. Поэтому представляет интерес исследование свойств параметров Р.-Г. в частных решениях уравнений Эйлера-Пуассона.
Данная статья посвящена изучению зависимостей от времени параметров Р.-Г. в решениях Бобылева-Стеклова, Лагранжа, Гриоли и Гесса, и исследованию структуры ИС в этих решениях.
1. Постановка задачи
Рассмотрим уравнения движения твердого тела под действием силы тяжести [1-3]
(1)
Здесь обозначено: ω=(ω1, ω2, ω3) − вектор угловой скорости; v=(v1, v2, v3) − единичный вектор, указывающий направление силы тяжести; A=(Aij) − тензор инерции; e=(e1, e2, e3) − единичный вектор 
, где O − неподвижная точка, C − центр тяжести тела; 
, где m − масса тела, g − ускорение свободного падения.
Уравнения (1) имеют первые интегралы
(2)
где E и k − произвольные постоянные.
Пусть θ,φ,ψ − углы Эйлера, введенные таким образом, что θ=<(e,v), φ − скорость собственного вращения вокруг вектора e, ψ – скорость прецессии вокруг вектора v. Тогда [8]
(3)
(4)
Если известно решение уравнений (1)
(5)
то углы Эйлера можно определить из (3), (4)
(6)
Параметры Р.-Г. выражаются через переменные (6) следующим образом [8]:
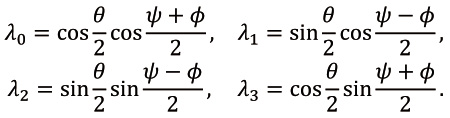(7)
Они удовлетворяют соотношению
(8)
Если известны параметры Р.-Г., то углы Эйлера определим из формул
(9)
а vi из равенств
(10)
Для записи уравнений (1) в параметрах Р.-Г. необходимо в эти уравнения подставить значения (10). Например, в главной подвижной системе координат уравнения Эйлера-Пуассона (1) принимают вид
(11)
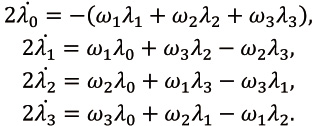(12)
Уравнения (11) с помощью формул
(13)
можно привести к системе трех дифференциальных уравнений на параметры λ1, λ2, λ3 [5,7].Интегралы (2) преобразуются очевидным образом на основе (10).
2. Решение Бобылева-Стеклова
Пусть в уравнениях (1) e=(1,0,0), A=diag(2A2,A2,A3), а в интегралах (2) значения постоянных таковы:
где x, H − параметры.Тогда уравнения (1) допускают решение [9] (поскольку формулы (3), (10) для параметров Р.-Г. записаны в другой системе координат по сравнению с рассматриваемым решением, то для новых переменных используем “~”)
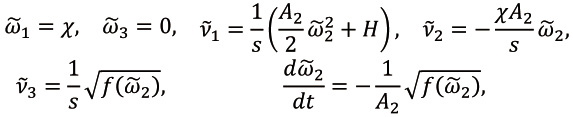(14)
где
(15)
Из (14) следует, что подвижный годограф вектора угловой скорости − отрезок прямой.
Опуская знак “~” представим решение (14), (15) в эллиптических функциях, используя систему координат, в которой записаны соотношения (3)– (6):
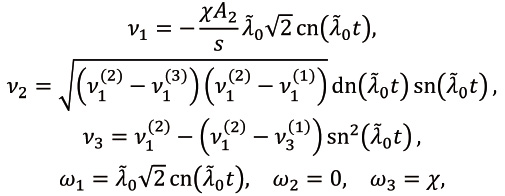(16)
где
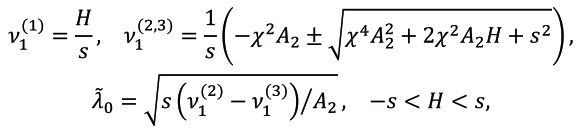(17)
а переменная v3 изменяется в промежутке 
, где эти значения указаны в формулах (17).Эллиптические функции (16) имеют модуль
(18)
Для нахождения параметров Р.-Г. в решении Бобылева-Стеклова воспользуемся соотношениями (6) и (16)
(19)
(20)
(21)
Зависимость параметров 
от времени найдем из соотношений (7) с учетом формул (19)-(21).Обозначим
(22)
С помощью (22) из равенств (19), (20) определим ИС на параметры Р.-Г. для случая Бобылева-Стеклова:
(23)
где 
− сопряженный к k1 модуль эллиптических функций.Итак ИС (23) является многочленом по параметрам Р.-Г. восьмого порядка.
Последняя формула из системы (21) представляет интерес, поскольку из неё следует достаточно наглядное представление скорости прецессии от угла собственного вращения тела
ИС для компонент вектора угловой скорости в силу (14) имеет линейный характер.
3. Сферический гороскоп (изоконические движения)
Рассмотрим тяжелое твердое тело, эллипсоид инерции которого является сферой: A3=A2=A1 Выбором системы координат можно принять s2=s1=0. Тогда из (1), (2) имеем
(24)
(25)
(26)
(27)
Изучим изоконические движения сферического гироскопа [2,4].Для этих движений подвижный и неподвижный годографы вектора угловой скорости симметричны относительно касательной плоскости к аксоидам. При этом необходимым и достаточным условием является ИС
(28)
где c − единичный вектор, неизменно связанный с телом. Положим c=(0,0,1)[4]. Тогда из (28) следует
(29)
Уравнения (24), (25) и интегралы (26) описывают движение гироскопа Лагранжа для случая сферического распределения масс. Из третьего уравнения системы (24) получим ω3=c*, где c* − произвольная постоянная. Потребуем, чтобы (29) было следствием (27). Тогда для ω3 имеем следующее значение
(30)
В [4] показано, что, если компоненты угловой скорости заданы в виде (3), то (29) выполняется при условии, когда в соотношениях (3) ψ=φ. Сравнивая (3) и (30), получим
(31)
Для получения уравнения на функцию θ(t) воспользуемся первым уравнением из (26) и соотношениями (3)
(32)
где 
, 
,
.
При преобразовании решения уравнения (32) к эллиптическим функциям запишем его в виде
(33)
Без ограничения общности считаем s>0. Тогда переменная v3 изменяется в промежутке
(34)
Из уравнения (33) в силу (31) получим
(35)
где sn(ɡt) − эллиптическая функция с модулем k2 и параметром ɡ, имеющими следующие значения
(36)
Таким образом, на основании (35) и равенства v3 =cos θ можно записать
(37)
Функцию φ(t) определим из (31) в силу (35)
(38)
В случае изоконичных движений сферического гироскопа для параметров Р.-Г. из (7) получим
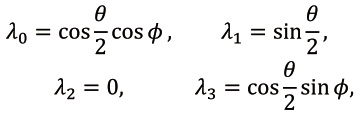(39)
где функции 
находятся из (37), а функция φ(t) из (38), в которых необходимо учесть равенства (36). Таким образом для рассматриваемых движений найдены зависимости параметров Р.-Г. от времени − соотношения (39). Из них следует, что одно ИС имеет линейный вид. Другое ИС для уравнений (11) тоже линейное, но оно линейно по отношению к компоненте ω3. Следовательно, в случае сферического гиростата для этих уравнений имеем два линейных ИС по отношению к переменным задачи.
4. Решения, описывающие прецессионные движения тела
В динамике твердого тела особую роль играют решения, которые характеризуются прецессионными движениями тела. В книге [4] показано существование прецессий тела относительно оси, не совпадающей с вектором v.
Пусть ось l1 с единичным вектором a и с началом в неподвижной точке неизменна по отношению к телу и составляет постоянный угол θ0 с осью l2, которая неподвижна в пространстве. Обозначим через γ − вектор, принадлежащий оси l2. Для прецессий выполнятся следующие кинематические уравнения [4]
(40)
где
(41)
Класс прецессий твердого тела, имеющего неподвижную точку, характеризуется инвариантными соотношениями [4]
(42)
Если неподвижную систему координат связать с вектором a, то есть третью ось её направить по вектору a=(0,0,1), то имеют место cоотношения
(43)
Они удовлетворяют кинематическому уравнению для вектора γ из (40) и соотношению γ2=1 из (41). Для вектора v в [4] получено следующее разложение
(44)
Когда вектор v имеет вид (44), а вектор γ − (43), то кинематическое уравнение для v из (40) становится тождеством.
При рассмотрении прецессий относительно наклонной оси параметры Р.-Г. можно найти по аналогии с (3), (4), (7). То есть в дальнейшем полагаем
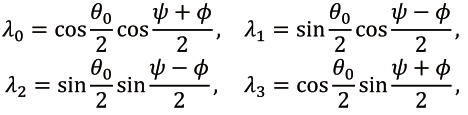(45)
где углы θ0, ψ, φ − углы Эйлера, введенные с помощью неподвижной системы координат, которая связана с вектором γ, (но не с вектором v, как ранее).
Пример 1 − Решение Д. Гриоли. Пусть в уравнениях (1) e=(0,0,1), компоненты тензора A удовлетворяют равенствам
(46)
параметр S имеет значение
(47)
Тогда при выполнении (46), (47) уравнения (1) допускают решение Д. Гриоли[13], которое запишем в обозначениях [4]
(48)
(49)
характеризующееся регулярной прецессией тела относительно наклонной оси (угол между этой осью и вектором γ приведен выше, а угол θ0 = π/2).
Указанное свойство можно доказать следующим образом. На основании решения (48), (49) получим, что вектор γ с компонентами в подвижном пространстве
(50)
не изменяет своего положения в неподвижном пространстве. В процессе движения выполняется инвариантное соотношение e·γ=0, то есть вектор e перпендикулярен вектору γ (θ0 = π/2). Угловая скорость тела в силу соотношений (50) в векторном виде такова:
(51)
Из формулы (51) следует, что в (42), (45) ϕ=ψ=m. Выберем неподвижную систему так, что ϕ=ψ=mt (t − время). Подставив θ0 = π/2, ϕ=ψ=mt в соотношения (45) имеем
(52)
Из (52) следует, что имеют место два линейных ИС на параметры (45). Для получения зависимостей компонент вектора v от параметров Р.-Г. подставим cosmt, sinmt из (52)в (49):
(53)
при этом компоненты ωi из (48) выражаются через параметры Р.-Г. следующим образом
(54)
Соотношения (53), (54) являются решением уравнений (1), если в них учесть условия (46), (47).
Пример 2 − Решение В. Гесса. Как показал А. Брессан[12], в решении В. Гесса[14] при нулевом значении постоянной интеграла моментов из (2) имеет место прецессия относительно горизонтальной оси. То есть
(55)
и в формуле (44) χ0=π/2, θ0 = π/2. Для записирешения, описывающего данную прецессию, воспользуемся введенной выше системой координат e=(0,0,1). Пусть компоненты тензора Aij удовлетворяют условиям [4]
(56)
Следуя обозначениям [4], имеем
(57)
(58)
(59)
где
(60)
Выпишем решение уравнений (60). Из первого уравнения данной системы имеем [4]
(61)
где c − произвольная постоянная. Формулы (57) − (59) характеризуют все переменные задачи (1).
Для нахождения решения ψ(t) из второго уравнения системы (60) положим
(62)
Тогда из (60), (62) получим
(63)
где μt, snμt, cnμt − эллиптические функции, имеющие модуль k3 из (62). Параметры Р.-Г. имеют вид
(64)
где функции ψ(t), φ(t) выражаются из формул (61), (63). Представляет интерес вид ИС для прецессий Брессана-Гесса. Используя (9), (64) и (61), (63) найдем
(65)
(66)
Таким образом, в случае прецессии относительно горизонтальной оси гироскопа Гесса для параметров Р.-Г. имеет место два квадратичных ИС (65) и одно ИС трансцендентного вида (66).
Заключение
Исследованы свойства параметров Р.-Г. в решениях уравнений Эйлера-Пуассона, моделирующего движение тяжелого твердого тела, в случаях Бобылева-Стеклова, Лагранжа, Гриоли и Гесса. Полученные результаты могут быть применены в истолковании движения тела.
Автор выражает благодарность профессору Г.В. Горру за внимание к работе.