Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,556

• Авторы
• Файлы

Фурменко А.И. 1 Веневитина С.С. 1 Зенина В.В. 1

---

1 ФГБОУ ВО «Воронежский государственный лесотехнический университет им. Г.Ф. Морозова»

Статья в формате PDF

878 KB

При изучении качественных свойств решений дифференциальных уравнений на группах Ли, часто возникает необходимость рассмотреть семейства операторов вида

,

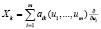где 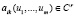. Если функции 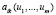удовлетворяют ряду свойств, то в совокупности операторов 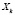можно задать операцию коммутирования

,

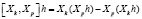которая вводит в совокупности структуру конечномерной алгебры Ли 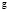. Рассматривается случай, когда функции 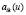представляют собой многочлены переменных 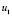, 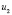степени не выше второй. Операторы имеют вид

+,

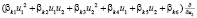где 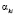, 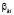– константы. Из предположения, что операторы 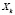соответствуют базисным элементам трехмерной алгебры g, и с учетом стандартного соотношения 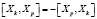определим трехмерную алгебру Ли дифференциальных операторов указанного вида с базисными операторами:

, , .

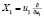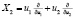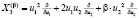Можно проверить, что при любом значении коэффициента 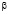определено семейство алгебр Ли с коммутационными соотношениями:

, , .

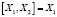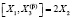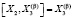Библиографическая ссылка