В условиях интенсивного внедрения в практическую деятельность инноваций одним из перспективных направлений повышения эффективности управленческой деятельности является использование эконометрического моделирования, позволяющего осуществить количественный и качественный анализ взаимосвязанных финансово-экономических показателей [1, 3]. Корреляционно-регрессионная зависимость экономических данных, имеющая место в силу причинно-следственных отношений, позволяет выявить и обосновать ряд характеристик, способствующих повышению эффективности управленческих решений.
Эконометрическое моделирование, базирующееся на корреляционно-регрессионной зависимости признаков, позволяет не только выявить и формализовать форму связи между разнородными экономическими показателями, но и осуществить прогноз дальнейшего развития объекта (системы, процесса) исследования [2].
Одним из основных направлений эконометрического моделирования является построение моделей парной и множественной регрессий, обладающих высоким качеством, с целью дальнейшего их использования для анализа и прогнозирования динамики экономических процессов в условиях экономической неопределенности [4]. Проблема построения регрессионных моделей высокого качества в значительной степени зависит от правильной спецификации модели, которая в дальнейшем определяет все свойства теоретической модели и возможность ее использования для построения прогнозов. Как правило, спецификация регрессионной модели предусматривает решение нескольких проблем: во-первых, анализ исходных статистических данных с целью выбора и обоснования результативного и факторных признаков; во-вторых, определение вида регрессионной модели, в максимальной степени отражающей реальные свойства совокупности статистических данных, подлежащих исследованию.
Эконометрические модели, базирующиеся на исследовании корреляционно-регрессионной зависимости экономико-статистических данных, находят широкое применение в экономических и технико-экономических исследованиях, посвященных проблемам эффективного менеджмента [7]. Каждой области экономических исследований, связанной с анализом эмпирических данных, как правило, соответствуют свои эконометрические модели [6].
Определение результативного и группы факторных признаков, участвующих в построении регрессионной модели, целесообразно осуществить в два этапа: первоначально эндогенная (зависимая) и экзогенные (независимые) переменные выделяются на основании экономического анализа существа проблемы, сопряженной с целью исследования; затем дальнейшее обоснование выбора результативного и факторных признаков осуществляется, используя математический аппарат, в частности, экономико-математический анализ матрицы парных корреляций. Элементы матрицы парной корреляций являются коэффициентами парных корреляций, характеризующих тесноту взаимной связи признаков, и определяются следующим соотношением
=
= 
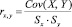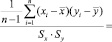
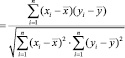, (1)
где y, xi – значения признаков, состоящих в корреляционной зависимости,
Sx и Sy – оценка дисперсий признаков, характеризующих вариабельность этих переменных , т.е. степень их разброса относительно среднего значения.
Оценка дисперсии признаков может быть выполнена следующим образом
,
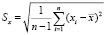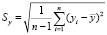. (2)
где n – длина временного ряда исследуемых признаков.
Коэффициент парной корреляции колеблется в пределах от – 1 до + 1, чем ближе его значение, взятое по модулю, к единице, тем более тесной признается корреляционная взаимосвязь между признаками. Положительная или отрицательная корреляция между признаками находит свое отражение в знаке коэффициента парной корреляции.
Величина коэффициента парной корреляции сама по себе еще не свидетельствует о статистической значимости влияния выявленного факторного признака на результативный признак. Для уточнения данного момента используется t-критерий Стьюдента, который может быть определен следующим образом
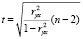. (3)
При сравнении рассчитанного значения критерия Стьюдента с табличной величиной можно судить о статистически значимой корреляционной связи между признаками.
Для подтверждения правильности выбора группы факторных признаков для построения регрессионной модели целесообразно оценить коэффициент множественной корреляции, характеризующий влияние множества факторных признаков на результативный признак
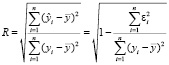. (4)
Коэффициент множественной корреляции может быть рассчитан для различного набора факторных признаков и, таким образом, можно получить линейку величин для уточнения корреляционно-регрессионной зависимости и набора факторных признаков.
Построение регрессионной модели является творческим процессом, опирающимся на серьезные знания в области экономической теории, макро- и микроэкономики, эконометрического анализа и должно быть индивидуально в каждой конкретной ситуации [5].
После определения результативного и факторных признаков необходимо перейти ко второму этапу спецификации регрессионной модели, т.е. к выбору вида модели. В зависимости от целей и задач моделирования, а также практических аспектов прикладного исследования предварительно может быть очерчен широкий круг регрессионных моделей, в котором могут быть учтены линейные и нелинейные, парные и множественные корреляционно-регрессионные зависимости, подлежащие построению и дальнейшему исследованию. В предположении о наличии между исследуемыми признаками линейной зависимости общий вид регрессионной модели, содержащей произвольное количество факторных признаков, выглядит следующим образом
y(t) = a0 + a1 x1(t) + a2 x2(t) +…+
+ ak xk(t) + e (t), (5)
где y(t) – эндогенная переменная,
xi(t) – экзогенные переменные,
e(t) – случайная компонента, характеризующая стохастическую природу экономических данных.
В случае выбора в качестве факторного признака только одного показателя можно получить частный случай модели множественной регрессии – модель парной регрессии.
Кроме линейной зависимости между признаками может иметь место и нелинейная взаимосвязь. В этом случае целесообразно построить комплекс моделей нелинейного вида. Окончательный выбор того или иного вида модели базируется на анализе показателей качества регрессионной модели [8]. В первую очередь, необходимо выполнить расчет и анализ коэффициента детерминации, характеризующего общее качество построенного уравнения корреляционно-регрессионной зависимости. Для расчетов может быть использована следующая формула
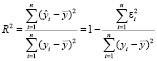. (6)
Коэффициент детерминации характеризует долю дисперсии результативного признака, учтенного в модели регрессии с определенным набором факторных признаков. Величина коэффициента детерминации варьирует в пределах от 0 до 1 и чем ближе ее значение к единице, тем большее значение вариации результативного признака обусловлено вариацией факторных признаков, включенных в модель регрессии. Между коэффициентом детерминации и коэффициентом множественной корреляции существует однозначная зависимость
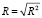. (7)
После оценки общего качества уравнения регрессии, характеризуемого коэффициентом детерминации, целесообразно оценить статистическую значимость построенного уравнения регрессии, используя критерий Фишера, выраженный следующим соотношением
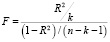, (8)
где k – количество факторных признаков, участвующих в построении модели множественной регрессии.
По итогам сравнения расчетного и табличного значения F-критерия Фишера можно сделать выводы о статистической значимости построенного уравнения регрессии [10]. Рекомендуется построить несколько видов регрессионных моделей с различным набором факторных признаков и, оценивая критерий Фишера для различных наборов факторных признаков, можно сделать вывод о наиболее приемлемом наборе экзогенных переменных, характеризующих корреляционно-регрессионную зависимость исследуемых признаков.
Для уточнения целесообразности включения в регрессионную модель конкретного факторного признака рекомендуется оценить статистическую значимость соответствующего коэффициента регрессии, характеризующего значимость влияния факторного признака на результативный признак. Критерий Стьюдента в оценке статистической значимости коэффициента регрессии при факторном признаке имеет вид
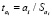, (9)
где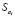 
– это стандартное (среднеквадратическое) отклонение коэффициента уравнения регрессии ai. Величина 
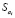представляет собой квадратный корень из произведения несмещенной оценки дисперсии 
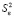и i -го диагонального элемента матрицы, обратной матрице системы нормальных уравнений.
Если расчетное значение t-статистики Стьюдента не превосходит табличного значения критерия, то оцениваемый коэффициент регрессии и соответствующий ему факторный признак не признаются статистически значимыми, и такой факторный признак рекомендуется из регрессионной модели исключить. При этом качество построенной регрессии существенно не ухудшится. Если же расчетное значение t-статистики Стьюдента превосходит пороговое табличное значение, то коэффициент регрессии и соответствующий факторный признак признаются статистически значимыми и такой фактор целесообразно оставить в регрессионной модели.
Количество факторных признаков, составляющих модель регрессии, может быть определено исходя из следующих соображений: целесообразности при осуществлении дальнейших вычислений, например, построении прогноза, и интерпретации полученных результатов исследования. Теоретически в модель регрессии может быть включено произвольное количество экзогенных переменных, но слишком большое их количество приведет к неустойчивости модели, ее сверхчувствительности и затруднит вычислительный процесс и дальнейшую интерпретацию результатов. При использовании для анализа и прогнозирования экономико-статистических данных современных информационных технологий эта проблема может быть частично нивелирована.
Одной из основных целей моделирования корреляционно-регрессионных зависимостей экономико-статистических данных является построение прогнозов и определение перспектив развития системы (процесса). Расчет прогноза исследуемых показателей с определенной долей вероятности будет способствовать принятию правильного, своевременного, научно обоснованного управленческого решения на основании информации, полученной по регрессионной модели.
При построении точечного прогноза в уравнение регрессии необходимо подставить прогнозные значения всех экзогенных переменных, участвующих в построении регрессии. При использовании специализированных программ статистического анализа и прогнозирования экономических данных, таких как Statistica, SPSS, Vstat, Stadia, Олимп: СтатЭксперт и т.д. данная проблема существенно упрощается [9].
Для определения интервального прогноза необходимо рассчитать ширину доверительного интервала, зависящую от вероятности расчетов, заданной точности прогнозирования, длины временных рядов признаков, составляющих информационную базу исследования, количества шагов упреждения. Для расчета доверительного интервала может быть использовано следующее соотношение
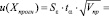
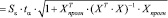, (10)
где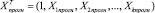 
,
Sε – среднее квадратичное отклонение, определенное исходя из остаточной дисперсии и характеризующее точность построения прогноза, tα – статистика Стьюдента, характеризующая вероятность расчетов.
Необходимо отметить, что прогнозирование имеет вероятностный характер и отражает сложившиеся закономерности лишь при сохранении в периоде упреждения закономерностей и тенденций, имеющих место в анализируемом периоде. К тому же, прогнозирование имеет рекомендательный характер, помогающий принять правильное управленческое решение с учетом сложившихся реалий, исходя из целей деятельности и с учетом субъективных предпочтений лица, принимающего решения. Тем не менее, построение моделей корреляционно-регрессионной зависимости ряда экономико-статистических показателей и последующее определение их прогнозных значений поможет глубже понять причинно-следственные связи признаков, а, следовательно, будет способствовать принятию рационального, математически и научно обоснованного управленческого решения, и, в конечном счете, будет способствовать повышению эффективности бизнеса.