Электростатический гироскоп (ЭСГ) с шаровым ротором представляет собой трех степенной свободный гироскоп, который благодаря наличию регулятора поддерживающей силы можно также использовать в качестве ньютонометра для измерения ускорений движущихся объектов [1].
Основным достоинством неконтактного подвеса ротора является практическое полное отсутствие сил трения при его вращении. Это открывает принципиальную возможность повышения точности гироскопических приборов. Существенным преимуществом ЭГС является возможность его использования при неограниченных углах поворота летательного аппарата вокруг центра тяжести без каких либо дополнительных устройств типа карданова подвеса. В этом случае корпус гироскопа устанавливается на движущемся объекте, совершающем произвольное движение [1–3].
Активные исследования навигационных датчиков с электростатическими подвесами ведутся в США (Honeywell, Stanford University), Франции (Sagem), Китае (Tsinghua Jiaotong Universities) и в Росcии (ЦНИИ Электроприбор, МИЭА, РПКБ, Институт прикладной механики) [4].
В работах [5] проводится анализ проблем создания гироскопа с электрическим подвесом. Даются рекомендации по выбору материала. Проводятся данные о величинах деформации ротора при действии центробежных сил.
ЭСГ имеет ряд преимуществ по сравнению с другими датчиками ИНС: высокая точность (до 10-10I/с), длительная безотказная работа на выбеге ротора (до нескольких лет), малое энергопотребление1 (до нескольких ватт), небольшие габариты и масса. ЭСГ мало подвержен износу, вследствие чего надежность прибора в основном определяется надежностью и сроком службы электронных элементов. Опыт эксплуатации ЭСГ на морских объектах подтвердил высокую точность и достаточную надежность корабельных ИНС на ЭСГ [6].
Использование ЭСГ на космических аппаратах привлекательно по той причине, что в условиях космоса легче поддерживать необходимую степень вакуума в гироскопе, решать задачу поддержании ротора во взвешенном состоянии, снизить энергопотребление системы. Вместе с тем, использование ЭСГ в условиях космического пространства требует решении комплекса новых задач, как в области теории, так и в области высоких технологий.
Технологические проблемы обработки поверхности ротора с точностью до 0.1 мкм оказывается весьма сложными и требуют создания специального оборудование[5]. В силу того, что первая гармоника формы ротора описывает его дисбаланс, то далее термин не сферичность ротора будет рассматриваться в обобщенном смысле и включать в себя и понятие несбалансированности ротора.
Ротор обрабатывается таким, чтобы после раскрутки до номинальной угловой скорости он в результате деформаций под действием центробежных сил принял форму сферы.
Поддержание вакуума внутри камеры до величины 1,3*10-6Па осуществляется ионно-геттерным насосом. Разгон ротора и демпфирование его нутационных колебаний, возникающих во время первоначальной раскрутки ротора, производится специальными катушками, которые после достижения ротором номинальной скорости отличаются на все время функционирования прибора.
Рабочая (номинальная) скорость вращения роторов в созданных образцах гироскопов составляет 12, 30, 60, 150, 180 тыс. об/мин. [45, 47]. Средняя величина зазора между ротором и электродами выбирается в пределах (3-40)*10-6м. Не сферичность внутренней поверхности полости не превышает (1-5)*10-7м. [46]. Диаметр ротора колеблется в диапазоне (30-70)*10-9м. для обеспечения вращения вокруг определенной оси и улучшения характеристик начальной выставки, ротор имеет в экваториальной области узкое утолщение, изготовленное из материала с боле высокой плотностью. Материал ротора выбирается с учетом способности сохранять форму, иметь достаточную упругость и малый удельный вес. Таким требованием лучше других материалов удовлетворяет бериллий (удельный вес 1,85*103 кг/м3) и алюминий (удельный вес 2,7*103 кг/м3).
При наличии не сферичности поверхности ротора возможно появление уходов из-за не сферичности электродов, смещений центра масс ротора в подвесе, возникающих при перегрузках и вибрациях основания и при отсутствии нулевого электрода, заполняющим междуэлектродное пространство подвеса и т.д. [7, 8].
Деформации ротора ЭСГ, вызванные центробежными силами после его раскрутки до номинальной скорости, могут приводить при перегрузках в 1 g к весьма большим возмущающим моментам и уходом ЭСГ до десятых долей градуса в час и более. В работе [5] рассматривается ротор ЭСГ, предназначенного для БИНС. Ротор выполнен в виде сферической оболочки с кольцевым утолщением в экваториальной плоскости. Уходы такого ротора в ЭСГ с шести электродным подвесом при произвольных положения оси вращения относительно электродов подвеса могут доходить до 2 градусов в час, если не проводить дополнительной обработки поверхности ротора, придавая ему специальную форму с тем, чтобы после раскрутки поверхность ротора становилась сферической (предварительная «асферизация ротора»). Заметим, что в шести электродном подвесе основной вклад в уход ЭСГ вносят четвертая и в меньшей степени восьмая «гармоники» разложения поверхности ротора в ряд по полиномам Лежандра. В задаче, исследованной в [9], уводящие моменты при учете только второй гармоники имеют величину 0.20 градусов в час, при учете второй и четвертой гармоник – 1,5 градусов в час, при учете всех слагаемых до восьмой гармоники включительно – 1,6 градусов в час, учет последующих членов ряда может привести к уходам до 2 градусов в час.
Основная часть. Рассмотрим ротор электростатического гироскопа, в экваториальной области которого находится поясок, имеющий плотность, отличную от плотности шара. Предложим, что магнитное поле внутри кожуха отсутствует , вакуум идеальный и сам кожух гироскопа неподвижен. Центральный эллипсоид инерции ротора есть эллипсоид вращения [5]. Неравенство моментов инерции обеспечивается за счет узкого кольцевого пояска в экваториальной области ротора, изготовленного из материала с более высокой плотностью.
Тогда моменты инерции ротора относительно главных осей определяются формулами
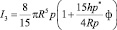
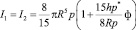
где ρ* – плотность материала пояска, h, ф – толщина и угол, определяющий размеры пояска.
Формулы (1) были получены в предположении, что угол ф мал. Для реальных конструкции ф составляет 10 °÷20 °. Из соотношения (1) получаем
.
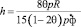Здесь
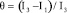. (2)
Если взять бериллиевый ротор с титановым пояском (для титана плотность ρ* = 5.2 г/см3) и угол ф = 15 °, a ϑ = 0.1 то для толщины титанового пояска имеем h = 0.1 R.
Рассмотрим деформированное состояние ротора без учета пояска.
Используя закон сохранения массы имеем,
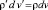(3)
где ρ’, v’ – плотность и объем ротора после деформации, ρ, v – до деформации; После деформации ротора получаем для элементарного объема dv’ соотношение
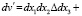
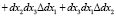. (4)
Здесь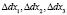 
– приращения линейных размеров элементарного объема dv после деформации вдоль осей x соответственно. Подставляя (4) в (3), после необходимых преобразований найдем
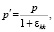
где
.
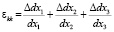Момент инерции ротора относительно оси х3 после его деформации определяется по формуле
.
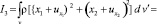
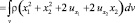Данное выражение получено при помощи соотношения (5) и преобразовано с учетом малости компонент вектора перемещений.
Переходим к сферической системе координат и после некоторых преобразований получим выражение для момента инерции
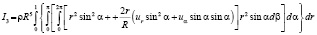(6)
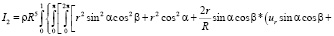
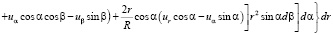(7)
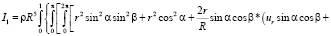
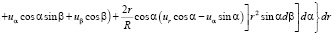
При расчетах обычно используется разности моментов инерции, поэтому обозначая
через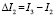 
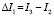получим
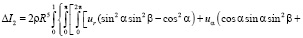
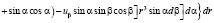(8)
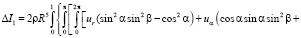
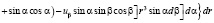
В результате подстановки
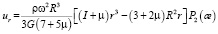
в последнее выражение (8) и после необходимых вычислений приходим к соотношению
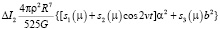(9)
Для бериллиевого ротора радиусом R = 0.5 см, при ω = 3000 об⁄с, ϑ = π⁄2, имеем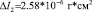 
. Этот числовой результат был получен после осреднения последней формулы по времени. Разность моментов инерции 
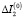до деформации этого ротора в реальных конструкциях имеет следующий порядок 
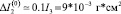. Сравнивая ∆I2 и 
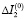, можно сделать вывод, что изменением момента инерции шара, обусловленного наличием деформации можно пренебречь. Вычисляя интеграл ∆I1 можно убедиться, что 
.
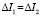Теперь вычислим моменты инерции пояска относительно осей координат xi
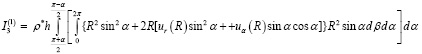
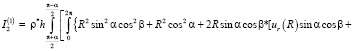
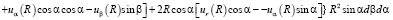(10)
.
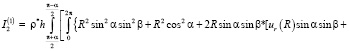
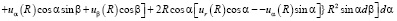Здесь
;
;
.
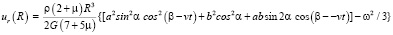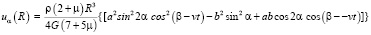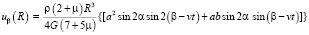Введем обозначение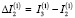 
, и, воспользовавшись (10) для разности моментов инерции, имеем
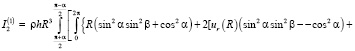
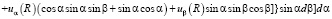. (11)
Подставляя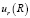 
, 
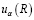и 
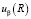в последнее выражение (11) и интегрируя по углам α и β, окончательно получим
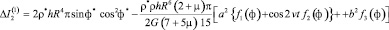. (12)
Здесь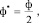 
;
.
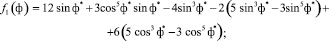
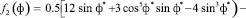
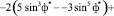
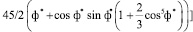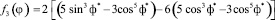Учитывая малость угла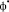 
, в данных соотношения можно положить 
, 
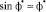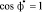и ограничиться линейными слагаемыми по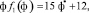 
.
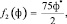
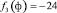Для числовой оценки влияния деформации на разность моментов инерции пояска вычислим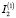 
по последней формуле (12) 
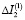, при рассмотренном выше случае
.
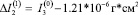Порядок разности моментов инерции до деформации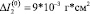 
. Сравнивая 
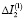и 
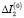, можно сделать вывод, что изменением момента инерции пояска, обусловленного наличием деформации можно пренебречь.
Влияние пояска на деформацию ротора оценим в случае его осесимметричного вращения. Пренебрегая изменением упругих характеристик в зоне прикрепления пояска, заменяем его влияние на ротор инерционной нагрузкой
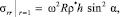
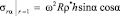, (13)
.
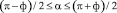На остальной поверхности ротора напряжения равны нулю.
Разложим правые части (13) граничных условий в ряд по полиномам Лежандра
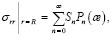
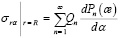(14)
Коэффициенты этих разложений определяются по формулам [56]
,
.
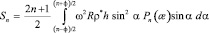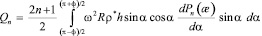Решение уравнений Ляме в осесимметричном случае известно и имеет вид
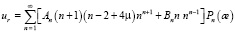
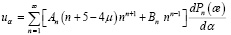(15)
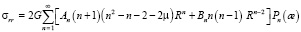
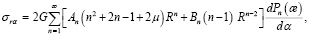
где постоянные интегрирования An и Bn находится при удовлетворении граничных условии (13).
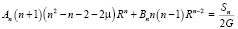(16)
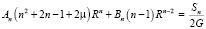
При n = 2 для коэффициентов разложения в ряд по полиномам Лежандра имеем
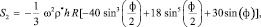(17)
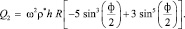
После подстановки (17) в (16) найдем коэффициенты системы уравнений при n = 2:
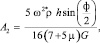
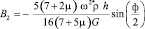. (18)
Воспользовавшись (13) и (18), находим уравнение радиальной деформации поверхности ротора, вызванное наличием кольцевого пояска в случае его осесимметричного вращения
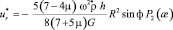. (19)
Для количественной оценки влияния пояска на деформацию ротора в случае его осимметричного вращения определяем, воспользовавшись формулой
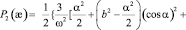
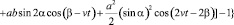
уравнение радиальной деформации поверхности ротора без учета кольцевого пояска
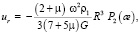
Затем вычислим отношение амплитудных значений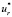 
к ur для ротора, физические и геометрические характеристики были описаны выше
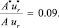(20)
Выводы
Из (20) видно, что наличие кольцевого пояска дает погрешность в вычислениях не более 10 процентов, следовательно,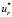 
, обусловленный пояском, несуществен. Поэтому при определении деформации ротора наличием пояска можно пренебречь.