В процессе синтеза комбинационной схемы дискретного устройства важной задачей является упрощение функций алгебры логики (ФАЛ) с целью получения такого вида формулы, при котором построенный в соответствии с ней автомат отличался бы минимальным расходом логических элементов на его изготовление. Строгое решение этой задачи должно учитывать конкретные особенности логических элементов применяемой элементной базы [1, 2].
Любая логическая функция может быть упрощена непосредственно с помощью аксиом и теорем логики, но, как правило, такие преобразования требуют громоздких выкладок. Кроме того, одна и та же функция может иметь множество различных представлений, которые в большинстве случаев не являются минимальными. Чем проще аналитическое выражение логической функции, тем удобнее и экономичнее реализовать ее практически на интегральных микросхемах.
Целью исследования является описание минимизации функции алгебры логики методом ненаправленного графа.
Материалы и методы исследования
Процесс упрощения булевых выражений не является алгоритмическим, поэтому более целесообразно использовать специальные методы минимизации, позволяющие проводить упрощение функции проще, быстрее и безошибочно. В настоящее время широко распространены следующие методы минимизации ФАЛ [1 – 3]:
1. Аналитический метод. В его основе лежит применение законов алгебры логики. Данный метод удобно использовать лишь для простых функций с количеством логических переменных не более четырех. При пяти и более переменных вероятность совершения ошибки при минимизации ФАЛ значительно возрастает.
2. Метод Квайна. Выполняется в два этапа. На первом осуществляется переход от канонической формы (совершенной дизъюнктивной или конъюнктивной нормальной формы) к сокращенной форме записи путем операций склеивания и поглощения, на втором этапе – переход от сокращенной формы к минимальной форме с помощью импликантной таблицы. Достоинство такого метода заключается в упорядоченности операций склеивания и поглощения, что уменьшает вероятность совершения ошибки.
3. Метод карт Карно. Это графический способ минимизации булевых функций. При использовании этого метода следует заданную ФАЛ представить в виде координатной карты и провести операции склеивания путем объединения в замкнутые области значений функции, равных логической единице, и исключить из выражения функции аргументы, изменяющие свои значения в пределах выделенных областей. Карты Карно можно рассматривать как определенную плоскую развертку n-мерного булева куба.
4. Геометрический метод. Основан на отображении функции n переменных в n-мерном пространстве (n-мерном кубе), каждая вершина которого сопоставляется с одним из наборов булевых аргументов. Наборы располагаются в таком порядке, что две соседние вершины отличаются знаком инверсии только одного аргумента. Решение заключается в объединении указанных закрашенных вершин и анализе полученных линий, площадей или параллелепипедов.
5. Гарвардский метод. Суть этого метода заключается в построении минимизирующей карты для функции от n переменных. Построение минимальной функции производится по специальному алгоритму.
Следует отметить, что в литературе по теории дискретных устройств отсутствует описание еще одного метода минимизации – метода ненаправленного графа.
Метод ненаправленного графа – это метод, основанный на теории графов, включающий в себя цифровые преобразования. Минимизация по указанному методу осуществляется по следующему алгоритму:
1. Выявить минтермы (наборы переменных), при которых функция обращается в логическую единицу.
2. Определить уровни графа (индексы) по количеству единиц в наборе.
3. Построить фрагмент графа с определением дуг, соединяющих вершины графа.
Построение графа является общим для всех графических структур.
Для того чтобы построить граф, необходимо определить основные его характеристики.
Общее количество вершин:
Nверш = 2n,
где n – количество переменных.
Количество уровней графа:
Nур = n + 1.
Количество вершин в уровнях определяется по формуле числа на одно сочетание:
Nву = Сni,
где i – номер уровня, i = 0, 1, 2, …, n.
Следует отметить, что для определения числа вершин в уровнях удобно использовать треугольник Паскаля (рис. 1).
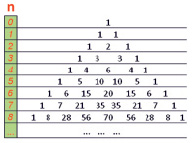
Рис. 1. Треугольник Паскаля
После того, как граф построен, необходимо соединить вершины, которые имеют между собой различие только в одной позиции.
Основным этапом минимизации ФАЛ по рассматриваемому методу является выявление замкнутых контуров. Если четыре вершины, соединенные между собой, представляют замкнутую геометрическую фигуру, то в результате минимизации получают две переменные. Если возможно объединить только две вершины, то получают три переменные. Если вершина не может быть соединена ни с одной другой, то ее буквенное обозначение будет полностью входить в результирующую запись. Результат (полученные минтермы) записывают через дизъюнкцию.
Одним из достоинств решения методом ненаправленного графа является возможность минимизации функций, с помощью заранее созданной заготовки. Для четырех переменных она имеет вид, представленный на рис. 2. При этом для решения не всегда требуется использовать полный граф, допускается построить его фрагмент (рис. 3).
Результаты исследования и их обсуждение
Рассмотрим пример. Пусть задана функция в виде:
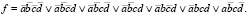
Функция зависит от четырех переменных, полный граф для нее представлен на рис. 2. Выполним построение интересующего нас фрагмента данного графа. Так как ФАЛ принимает значения логической единицы в записанных минтермах, то во фрагменте оставляем соответствующие вершины с номерами 0000, 0001, 0010, 0011, 0101, 0111, 1010 (для упрощения запишем их номера в десятичной системе счисления: 0, 1, 2, 3, 5, 7, 10 (рис. 3)).
На рис. 3 видно, что из полученного графа можно выделить два четырехугольника (0-1-3-2 и 1-3-7-5) и отрезок 2-10.
Из четырехугольника 0-1-3-2 видно, что общей частью всех вершин являются два первых нуля «00_ _». Также выделим общую часть вершин второго четырехугольника 1-3-7-5: «0_ _1»; общую часть вершин отрезка 2-10: «_010». Записав полученное выражение в буквенном виде, получим результат минимизации заданной ФАЛ:
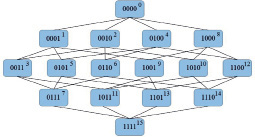
Рис. 2. Полный граф для функции четырех переменных
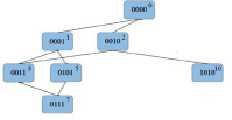
Рис. 3. Фрагмент графа для исследуемой ФАЛ
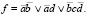 (1)
(1)
Выполним проверку аналитическим методом, используя законы и тождества алгебры логики.
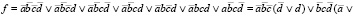
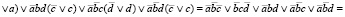
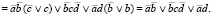 (2)
(2)
Сравнивая результаты решения (формулы (1) и (2)), можно сделать вывод об их совпадении.
Выводы
Следует отметить, что главным преимуществом рассмотренного метода перед другими является оперативность получения результата минимизации при количестве переменных более пяти.
При нахождении верной минимальной формы отсутствует необходимость в предварительном расчете неопределенных значений, если таковые имеются в функции.

