В настоящее время актуальность проблемы проектирования медицинских технологических процессов неуклонно увеличивается. Революционное совершенствование медицинских технологий, определяемое промышленной и технологической революциями, привело к тому, что искусность, как залог качества, была затребована в массовом количестве и уже не могла в той же мере опираться на мастерство одиночек. Сложность медицинских технологий потребовала для качественного исполнения команд, реализующих некий технологический процесс – медицинский технологический процесс, не сводимый к процессу, исполняемому одним человеком [1]. Медицинский технологический процесс – это система взаимосвязанных необходимых и достаточных научно-обоснованных лечебно-диагностических мероприятий, выполнение которых позволяет наиболее рациональным образом провести лечение и обеспечить достижение максимального соответствия научно прогнозируемых результатов лечения реальным при минимизации затрат [2].
Практическое внедрение теории медицинских технологических процессов испытывало определенные трудности, до тех пор, пока не стали активно разрабатываться системы их автоматизированного проектирования. Основным фактором, определяющим необходимость автоматизированного проектирования реализуемых в медицинской организации процессов, является отсутствие исчерпывающего описания большинства из них. Естественный путь решения этой задачи – использование прецедентной информации, например, экземпляров медицинских технологических процессов с доказательными хорошими параметрами качества, безопасности и результативности.
Каждый медицинский технологический процесс можно представить в виде графа, в вершинах которого находятся некоторые работы (операции, лечебные мероприятия), а ребра определяют порядок выполнения работ [3]. Как оказалось, медицинские технологические процессы, даже решающие одну и ту же задачу, могут различаться как порядком выполнения, так и составом работ, поэтому первым шагом является задача построения описания всего множества успешных медицинских технологических процессов, решающих одну и ту же задачу, т.е. такого графа, что граф каждого конкретного медицинского технологического процесса являлся бы его подграфом.
Для этой цели вводится понятие оператора переходов, т.е., по существу, правила (соответствующего некоторой работе), меняющего состояние процесса. Далее с помощью таких операторов определяются примеры или прецеденты потоков работ, тем самым уточняется понятие МТП. Далее строятся описания классов эквивалентности прецедентов. Наконец, описания классов эквивалентности используются для синтеза модели МТП, которая, в свою очередь, может служить основой для реализации МТП, их реинжиниринга, оптимизации по различным критериям и т.д.
Лечебные мероприятия и операторы
Пусть U множество слов конечной длины над некоторым алфавитом.
Зададим на U семейство алгебраических систем с сигнатурами, включающими одно-, двух- и n-местные отношения на U : P1 , P2. . . , Pm .
Для простоты будем полагать, что в сигнатуры входит ровно по одному отношению каждой местности. Каждую такую алгебраическую систему будем называть состоянием и обозначать через s. Множество всех состояний обозначим через E.
Элементы многоместных отношений будем далее называть фактами, элементы одноместных отношений признаками.
Если N – дискретное линейно – упорядоченное множество, то семейство отображений
O = {oi }, i = 1, . . . , M , O : E N > E,
таких что
o(s, n) = (s, n + 1),
где (s, n) = (z, n) ∪ (p, n) состояние системы
в точке n, z ⊆ Pi , (i = 2, . . . , m)- множество фактов, p ⊆ P1 – множество признаков, будем называть множеством операторов переходов.
Далее, множество N будем называть временем (дискретным), а для (s, n), (z, n), (p, n) используем более привычные обозначения: s(n), z(n) и p(n).
Если ⊆ P1 , ϕ ⊆ P2 ∪ · · · ∪ Pm , то оператор o ∈ O имеет вид:
o = o = <π, ϕ >, и s(n + 1) = o s(n),
где o s(n) = < z(n + 1), p(n + 1) >,
z(n + 1) = z(n) ∪ ϕ
либо
z(n + 1): = ϕ, p(n+1) = (p(n)∪π)
либо
p(n+1): = π.
В медицинском технологическом процессе каждому оператору o ставится в соответствие некоторое лечебное мероприятие.
Два разных способа действия оператора переходов o : o s(n) = < z(n + 1), p(n + 1) >, где z(n + 1) = z(n) ∪ ϕ либо z(n+1): ϕ и p(n+1) = ( p(n)∪π) либо p(n + 1): = π соответствуют двум различным способам изменения состояния: появлению в нем новых патологических процессов и признаков при сохранении имеющихся, либо исчезновению старых признаков и патологических процессов и появлению новых.
Если Ω(O) семейство последовательностей операторов вида ω = oi , oj , . . . , ok над множеством O операторов oj , где i, j, . . . , k элементы множества натуральных чисел N
и i < j < . . . < k, то каждую последовательность ω будем называть прецедентом или примером медицинского технологического процесса.
На Ω(O) зададим отношение эквивалентности ρ, порождающее фактор-множество
Ωr множества Ω(O).
Описанием G({ω}) каждого класса эквивалентности {ω} ∈ Ωr будем называть граф, такой что маршруты, порожденные всеми примерами ω ∈ {ω} являются его подграфами.
Классы эквивалентности медицинских технологических процессов и их построение
Внутри каждого из классов эквивалентности могут оказаться примеры, отличающиеся от других порядком следования операторов, порядком следования их групп, степенью их повторяемости и др. Эти различия приводят к появлению так называемых маршрутов: последовательного, параллельного, конкурентного, итеративного и условного в потоках работ [4] и необходимости представления таких маршрутов в G({ω}). Первые два вида маршрута были описаны в [5]. В клинической медицине в некоторых случаях допускаются различные последовательности лечебных мероприятий для лечения одной нозологической формы.
Для моделирования этого обстоятельства на множестве матриц инцидентности введем ассоциативную и коммутативную операцию покомпонентного сложения, сохраняющую единицу: На множестве матриц инцидентности графов введем ассоциативную и коммутативную операцию покомпонентного сложения, сохраняющую единицу: если А =[aij] и В = [bij] – матрицы инцидентности, то А + В = [сij], где сij = max {aij , bij}.
Пусть М(wj) – матрица инцидентности графа примера wj , через M(G) обозначим матрицу инцидентности графа G{w}.
Теорема 1. M(G) =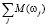 
, где суммирование в указанном выше смысле выполняется по всем примерам wj из класса {w}.
Эта теорема обосновывает процедуру построения описания класса.
Следующая теорема устанавливает, что, какой бы пример МТП мы ни взяли, если он принадлежит одному из классов, то он порождает хотя бы один из маршрутов, указанных выше.
Теорема 2. Для любого ω, если ω∈{ω}, то ω порождает хотя бы один из маршрутов в G({ω}).
Если с каждым оператором связать условие его применимости и состояние, к которому он применяется, то получим понятие прецедента медицинского технологического процесса: последовательность r = < (si, ci, oi), (sj, cj, oj), …,(sk, ck, ok) > будем называть прецедентом медицинского технологического процесса, если для каждых двух её элементов (sn, сn, on) , (sn+1 ,сn+1, on+1) справедливо сn+1on sn, где on sn – результат применения оператора on к состоянию sn, а – сn+1 условие применимости оператора on+1 к состоянию sn+1 .
Синтез медицинского технологического процесса по прецедентам
Моделью медицинского технологического процесса будем называть динамическую систему H = <X, N, >, где X – дискретное множество событий, N – линейно-упорядоченное дискретное множество, Ψ – функция переходов. Поскольку множество X определено выше (X = E), а в качестве N можно взять множество натуральных чисел, то задача построения модели медицинского технологического процесса сводится к восстановлению функции переходов Ψ.
Выше мы видели, что функция Ψ реализуется операторами из семейства O.
Это означает, что задача восстановления функции Ψ сводится к задаче восстановления операторов и условий их применения. Здесь надо заметить, что каждый из классов G(Ψ}) может содержать свое множество операторов, поэтому речь должна идти о восстановлении множества операторов в каждом из классов и последующем объединении этих множеств.
Решение этой задачи основано на анализе прецедентов медицинских технологических процессов. Поскольку эффект применения каждого из операторов содержится в параметрах π и ϕ (см. п. 1), то для восстановления оператора на основе прецедентов следует для каждого оператора найти эти параметры.
Сравним пары состояний si и si+1 для i = 1, . . . , M и рассмотрим два случая.
Случай 1: s i ∩ s i+1 ≠ ∅, тогда j = z i+1\(z i+1 ∩ z i ) , p = pi+1\ (p i+1 ∩ p i).
В частных случаях, когда имеет место включение в одну, либо в другую сторону, например s i ⊆ s i+1, получаем j = z i+1\ z i ,p = p i+1\ p i.
Случай 2: s i ∩ s i+1 = ∅ тогда z = z i+1i,p = p i+1.
Вершины графа G({ω}), в которых начинается любой маршрут, кроме последовательного, будем называть точками ветвления.
В них определяются условия применимости операторов. Пусть ρ и ρ′ прецеденты,
породившие параллельный маршрут в G({ω}), s0 состояние G({ω}) в точке ветвления, s и sρ и ρ′ следующие за s0 состояния прецедентов ρ и ρ′, соответственно.
Если говорить неформально, то для определения условий применимости операторов o и o′ следует сравнить состояния s и s′ прецедентов ρ и ρ′ и определить их различия, которые в простейшем случае и являются искомыми условиями применимости.
В более сложных случаях условия применимости операторов могут описываться логическими выражениями, например, в языке исчисления предикатов первого порядка. В этом случае условием применимости оператора является конъюнкция атомарных формул языка исчисления предикатов первого порядка, каждая из которых интерпретируется одним из сигнатурных отношений и выполняется на элементах, различающих s и s′.
Возвращаясь к Ψ, вспомним, что Ψ : X × N → X, так что для каждого состояния
si Y (si, n) = si+1 .
Поскольку функция переходов реализуется операторами, то Y восстанавливается следующим алгоритмом:
1. Выбрать оператор, условие которого выполняется в текущем состоянии si;
2. Применить оператор, т.е. построить состояние si+1 = o s i,
3. Перейти к п. 1.
Заключение
В статье кратко описан метод автоматизации построения модели медицинского технологического процесса по прецедентам. Такой путь является естественным для многих научных областей, в особенности для тех из них, где не существует точных моделей, а существующие модели при попытке применить их на практике оказываются недостаточно адекватными. Метод позволяет построить описание медицинских технологических процессов многопрофильного медицинского учреждения и на этой основе повысить эффективность работы всей организации.