В данной статье предлагаются методы решения классической задачи из школьного курса физики, описанной в замечательной книге «Задачи по физике», Библиотечка «Квант», выпуск № 5, 1980, И.Ш. Слободецкий, Л.Г. Асламазов [1]. Позволю себе привести полный текст задачи № 13: «За лисой, бегущей равномерно и прямолинейно со скоростью v1 гонится собака, скорость которой v2 постоянна по абсолютной величине и направлена все время на лису. В момент времени, когда скорости v1 и v2 оказались взаимно перпендикулярными, расстояние между лисой и собакой было равно l. Каково было ускорение собаки в этот момент?»
Мы в системе MathCAD будем решать похожие задачи, имеющие свое происхождение из указанной выше классической задачи. «Кролик» движется по случайной траектории. Его преследует «Лиса». Необходимо найти траекторию движения «Лисы», ее зависимость от времени. Вектор скорости «Лисы» направлен на «Кролика» и по модулю неизменен.
«Кролик» и «Лиса» движутся по плоскости
Пусть траектория движения «кролика» (рис. 1) описывается уравнением
,
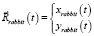а траектория движения «лисы»:
, 
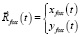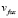– абсолютная неизменная величина скорости движения «лисы».
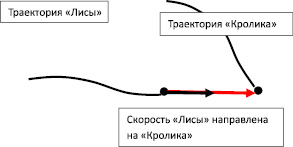
Рис. 1. «Кролик» движется по плоскости
Тот факт, что вектор скорости движения «лисы» направлен все время на кролика, и то, что абсолютная величина скорости движения «лисы» равна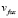 
, описывается системой уравнений (1.1):
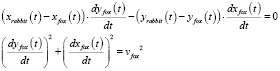(1.1)
где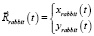 
– координаты траектории «кролика» на плоскости,
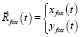– координаты траектории «лисы», 
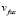– абсолютная величина скорости «лисы», t – время.
Система уравнений (1.1) относительно переменных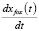 
, 
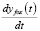имеет решение 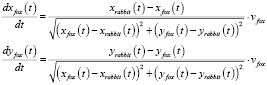(1.2):
(1.2)
Если бы траектория движения «кролика»
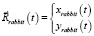
имела бы явную функциональную зависимость от времени, то данная задача в таком математическом пакете, как «MathCAD 15», реализуется в несколько операторов, подводящих ко встроенным решателям систем дифференциальных уравнений I порядка (rkfixed, Rkadaptи т.д.). По следующей ссылке [2] вы сможете скачать архивированный файл программы, выполненной в системе «MathCAD 15», по следующей ссылке вы сможете посмотреть анимированное изображение результатов работы данной программы [3].
«Кролик» и «Лиса» движутся по пересеченной местности
Произведем постановку задачи преследования «Лисой» «Кролика», двигающихся по пересеченной местности, заданной поверхностью Z = f(X, Y).Траектория движения «Кролика» задается уравнением
,
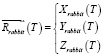где T – время движения «Кролика».
Необходимо найти траекторию движения «Лисы»
,
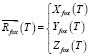при следующих условиях:
1. Горизонтальная проекция скорости движения «Лисы» на плоскость (X, Y) направлена на горизонтальную проекцию точек движения «Кролика» (рис. 1).
2. Скорости движения «Кролика» и «Лисы» неизменны и равны величинам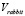 
, 
.
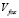Условия для решения поставленной задачи приводят к системе уравнений (2.1)
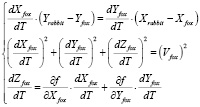. (2.1)
Первое уравнение системы (2.1) означает то, что горизонтальная проекция вектора скорости «Лисы»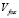 
на плоскость (X, Y) направлена на горизонтальную проекцию 
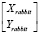текущего положения «Кролика». Второе уравнение означает то, что скорость передвижения «Лисы» равна постоянной величине 
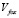. Третье уравнение получается из дифференцирования уравнения Z = f(X, Y) по времени T. Фактически, это означает то, что точка траектории «Лисы»
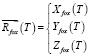
принадлежит поверхности Z = f(X, Y). Cистема уравнений (2.1) имеет решение в явном виде относительно переменных
, 
, 
:
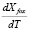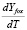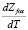(2.2)
При реализации задачи, рассматриваемой в данной статье, в математических пакетах, в частности в системе «MathCAD», мы предприняли следующее:
1. В системе «AutoCAD» была построена модель поверхности Z = f(X, Y) и был произведен импорт по горизонталям в текстовые файлы. Затем точки были обработаны в системе «MathCAD» и была произведена полиномиальная регрессия. На плоскости (X, Y) была построена дополнительная сетка для проведения двумерной сплайн-интерполяции и построения поверхносте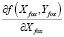й 
и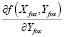 
, которые используются при решении системы уравнений (2.2).
2. В системе «AutoCAD» формируется массив горизонтальной проекции точек траектории «Кролика»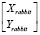 
. Далее, вводится формальный параметр t, чтобы мы могли построить параметрическую функцию
.
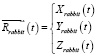Нами, в качестве формального параметра t, был выбран такой, который равномерно проходит через значения [0, … N – 1], где N – количество точек массива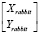 
. После выполнения сплайн-интерполяции функция траектории движения «Кролика» принимает вид
.
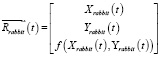Далее, производится параметризация формального параметра от длины дуги траектории движения «Кролика»:
.
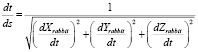Поскольку, длина дуги траектории «Кролика» может быть выражена: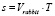 
, где T – это время движения «Кролика», то мы теперь можем в качестве основного параметра использовать время T.
3. Анимированное изображение движения «Кролика» нами предоставлено здесь [4].
4. При заданных стартовых позициях «Кролика» и «Лисы», при заданных значениях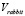 
и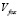 
было получено численное решение системы дифференциальных уравнений (2.2). С результатом анимации можно ознакомиться здесь [5]. На анимации видно, что при выбранных значениях «Лиса» догоняет «Кролика» несколько раз.
5. Полный листинг программы, выполненной в системе MathCAD с подробными комментариями можно посмотреть здесь [6].
6. Полный архив программы можно скачать здесь [7].
«Лиса» работает на опережение
Для прогнозирования «Лисой» движения «Кролика», мы предлагаем использовать следующую модель (рис. 2).
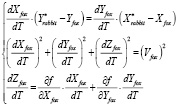, (3.1)
где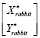 
– горизонтальная проекция вектора 
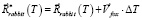(рис. 2). Здесь векторная величина скорости «Кролика» равна
.
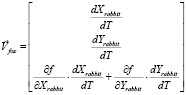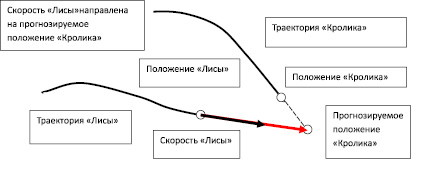
Рис. 2. «Лиса» прогнозирует движение «Кролика»
На выборе параметра приращения по времени ∆T остановимся подробнее. Введем следующую весовую функцию:
,
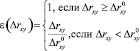где
,
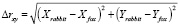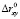– выбираемое нами пороговое значение дистанции между «Кроликом» и «Лисой». Измененный листинг программы в системе MathCAD вы можете просмотреть и скачать на сайте [7]. Анимированное изображение ситуации, когда «Лиса» бежит на опережение, вы можете посмотреть здесь (в проекции на плоскость [8] и трехмерный вид [9]).