Процесс облучения материалов быстрыми тяжелыми заряженными частицами сопровождается целым рядом физических эффектов, оказывающих влияние на их радиационную стойкость. К ним, в частности, относятся: образование каскадов и субкаскадов [4, 5, 7] движущихся атомов, сопровождающееся образованием точечных дефектов (вакансий и межузельных атомов), возникновение высоких температур и структурные изменения вблизи траекторий быстрых тяжелых заряженных частиц [1, 3, 6].
Теории образования треков в материалах, облучаемых быстрыми тяжелыми заряженными частицами и происходящим в них процессов, посвящено множество работ. Их можно разделить на две группы [1, 3, 6], первая из которых основана на модели «Тепловой вспышки», а другая – на модели «Кулоновского взрыва».
При торможении в материале быстрых тяжелых заряженных частиц с энергиями E > 1 МэВ/нукл. более 90 % их энергии передается в электронную подсистему за счет электронного торможения [2].
В модели ‹‹T-вспышки›› процесс разогрева трековой области и ионной подсистемы облучаемого материала вблизи траектории тяжелой частицы рассматривается как результат перекачки энергии от разогретой электронной подсистемы к ионной подсистеме материала в результате электрон-фононного взаимодействия [1, 3, 6].
В модели «Кулоновского взрыва» разогрев облучаемого материала рассматривается, как результат процесса электростатического расталкивания оголенных ионов в материале за характерное время существования обедненных электронами областей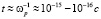 
(ωр – плазменная частота). Наиболее важной физической величиной при использовании модели «Кулоновского взрыва» и описании физических процессов, происходящих при облучении различных материалов потоками быстрых тяжелых ионов, является пространственно-временное распределение эффективного электрического поля вблизи траекторий быстрых тяжелых заряженных частиц. Корректный расчет эффективных электрических полей, формирующихся за времена их существования, и разогрева ионной подсистемы был представлен в работе [3].
В работе [6] был проведен сравнительный анализ разогрева материалов вблизи траекторий быстрых тяжелых заряженных частиц с использованием модели «Т-вспышки» и «Кулоновского взрыва». В рамках этих моделей были оценены изменения температур электронной и ионной подсистем в трековых областях при облучении аморфного сплава (Fe85B15) и меди быстрыми тяжелыми заряженными частицами (E > 1МэВ/нукл). Анализ полученных результатов показал [6], что использование модели «Кулоновского взрыва» для расчета разогрева электронной и ионной подсистем приводит к более сильному разогреву ионной подсистемы в трековой области и образованию области проплава по сравнению с аналогичными результатами, полученными в рамках различных моделей «Т-вспышки». Здесь же были проведены расчеты образования точечных дефектов в Cu в рамках использования моделей «Кулоновского взрыва» и «Т-вспышки». Сравнение результатов этих расчетов с экспериментальными данными показало [6], что модель «Кулоновского взрыва» более адекватно описывает образование треков в металлах по сравнению с «Т-вспышкой».
Однако в опубликованных ранее работах [3, 6] при использовании модели «Кулоновского взрыва» процессы релаксации электрического поля, которые приводят к уменьшению его величины, не учитывались.
Постановка задачи исследования
Для определения электрического поля необходимо решить следующее уравнение [3]:
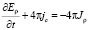, (1)
где Jp – плотность стороннего тока, а jc – плотность тока, возникающего под действием образующегося электрического поля. Значение тока jc определяется по формуле:
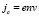(2)
где e – заряд электрона, n – концентрация электронов, v – их скорость под действием поля, которую в свою очередь можно определить из уравнения:
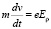(3)
m – масса электрона.
Подставив (2) в уравнение (1), получим:
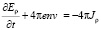(4)
Продифференцировав уравнение (4) по времени и используя (3), найдем:
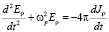, (5)
где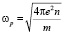 
– плазменная частота.
Проведение расчетов
Проанализируем полученные результаты для простой зависимости плотности стороннего тока, допускающей аналитические решения:
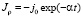(6)
где α–1 – характерное время существования стороннего тока.
В работе [3] пренебрегалось наличием тока, обуславливающего релаксацию электрического поля, и находилось решение уравнения
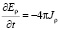(7)
Найдем решение уравнения (7). Для этого подставим (6) в (7) и получим:
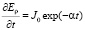(8)
где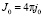 
.
Решение уравнения (8) с нулевым начальным условием определяется просто и имеет вид:
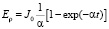(9)
При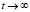 
, решение (9) выходит на постоянное значение
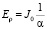(10)
Теперь при той же зависимости (6) найдем решение уравнения (5):
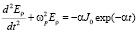(11)
Учитывая, что при t = 0
; 
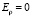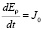, (12)
решение уравнения (11) легко определить:
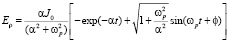(13)
где
; 
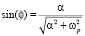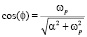(14)
При ωp = 0 выражение (13) переходит в (19). При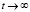 
выражение (13) принимает вид:
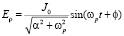(15)
Здесь, в отличие от постоянного значения (10), решение колеблется около нулевого значения.
Для дальнейшего анализа формулу (13) приведем к безразмерной форме относительно предельного значения (10) и представим в безразмерных переменных:
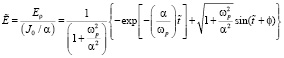(16)
где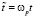 
– безразмерное время.
Далее, выражение (16) проиллюстрируем графически для нескольких значений безразмерного параметра 
(η = 0,5; 1,2; 2,0), то есть для случаев, когда импульс стороннего тока короче, равен или превышает по времени величину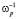 
(рис. 1). Отметим, что для каждого из указанных случаев ϕ можно определить по формулам (14).
Временем существования электрического поля можно считать время, за которое оно, возникая от нуля, существует до момента, когда оно первый раз снова обращается в нуль.
Проанализируем результаты, представленные на рис. 1. Без учета плазменных колебаний, как следует из (9) и (10), напряженность электрического поля за время порядка 1/α достигает постоянного значения, равного 1 (в безразмерных переменных).
При учете плазменных колебаний (рис. 1) значение напряженности электрического поля изменяется со временем, стремясь к нулю. При этом, чем меньше отношение характерного времени изменения электрического тока 1/α к характерному времени плазменных колебаний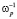 
(параметр 
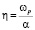), тем большего значения достигает напряженность электрического поля по отношению к стационарному значению, полученному без учета процесса релаксации (плазменных колебаний). Так из рисунков следует, что при увеличении η от 0,5 до 2, максимальное значение напряженности электрического поля составляет примерно от 70 % до 30 % от этой величины.
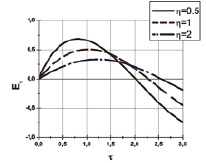
Рис. 1. Зависимость изменения безразмерной величины напряженности электрического поля в облучаемом материале от времени
Из результатов, полученных ранее [3], следует, что характерное время установления стационарного значения напряженности электрического поля будет меньше величины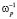 
(сравни кривые 3 и 4 на рис. 1 из [3]). Этот результат дает основание полагать, что учет релаксации напряженности электрического поля за счет плазменных колебаний не приводит к значительному уменьшению его амплитудного значения.
Оценим влияние процесса релаксации электрического поля на энергию, переданную ионам решетки в результате «кулоновского взрыва». Импульс, переданный иону решетки за время t, будет равен интегралу [3]:
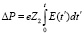(17)
где e – заряд электрона; Z2 – порядковый номер атомов мишени.
Подставив (9) в (17), получим значение импульса, передаваемого иону решетки, без учета процессов релаксации:
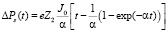(18)
Подставив (13) в (17), получим значение импульса, передаваемого иону решетки облучаемого материала, с учетом процессов релаксации:
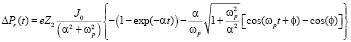(19)
За время, порядка времени релаксации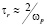 
(рис. 1) импульс, полученный ионом решетки без учета и с учетом процессов релаксации, принимает следующие значения:
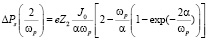(20)
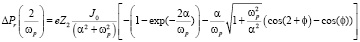(21)
В таком случае отношение энергии, полученной ионом решетки с учетом процессов релаксации, к значению энергии, полученной ионом решетки без учетов процессов релаксации, принимает следующий вид [3]:
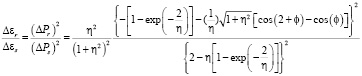(22)
где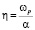 
, 
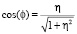(см. (15)).
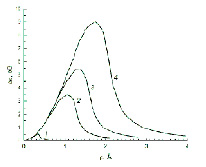
Рис. 2. Пространственное распределение кинетической энергии с учетом поправки на релаксацию, полученной ионами кристаллической решетки от электрического поля, возникающего вблизи траектории движения различных быстрых тяжелых ионов с энергией 10 МэВ/нуклон в железе: 1 – Z1 = 8, 2 – Z1 = 36 3 – Z1 = 54 4 – Z1 = 92
Анализ результатов расчетов
Проведем оценку влияния процессов релаксации электрического поля за счет возникающих плазменных колебаний на величину энергии, передаваемой ионам кристаллической решетки с учетом процессов релаксации. В работе [3] было показано, что после пролета тяжелой заряженной частицы в железе, в центральной области трека эффективный заряд ионов мишени будет составлять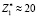 
. Это означает, что плотность положительного заряда в этой области будет равна ≈ 
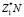, где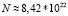 
см–3 – концентрация атомов железа. В таком случае плотность электронов, вытесненных из центральной области трека и участвующих в процессе релаксации, составит величину 
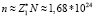см–3.
Используя это значение, для плазменной частоты получим: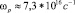 
или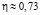 
. Оценка выражения (22) для значения 
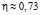дает следующий результат:
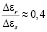. (23)
Таким образом, учет процессов релаксации приводит к тому, что величина энергии, переданной ионам кристаллической решетки от электрического поля с учетом процессов релаксации за счет плазменных колебаний, уменьшается примерно в 2,5 раза.
Результаты численных расчетов пространственного распределения кинетической энергии Δε, полученной ионами кристаллической решетки от электрического поля из [3] с учетом поправки на процессы релаксации приведены на рис. 2.
Таким образом, учет процесса релаксации показал, что количество энергии, переданной ионам кристаллической решетки от электрического поля, уменьшается примерно в 2,5 раза. Тем не менее, это значение все равно остается достаточно большим и будет составлять для кинетической энергии, передаваемой ионам облучаемого материала вблизи траектории быстрых тяжелых ионов, величину примерно равную от 1 эВ до 10 эВ, в зависимости от вида быстрого тяжелого иона.
Это может приводить к существенному разогреву кристаллической решетки вблизи траектории движущегося быстрого тяжелого иона, включая образование зон локального плавления, а также может способствовать необратимому выбиванию атомов из узлов решетки с дополнительным образованием точечных радиационных дефектов [6].