Расчеты проводились при следующих единицах измерения: килограмм-сила (кгс); сантиметр (см); секунда (с). Для перехода в другие единицы измерения были приняты следующие допущения: 1 кгс/см2 ≈ 0,1 МПа; 1 кгс с2/см4 ≈ 109 кг/м3.
Некоторая информация о моделировании нестационарных волн напряжений в деформируемых телах различной формы приведена в работах [1–10] .
В работах [1, 3–4, 7–8] приведена информация о физической достоверности и математической точности рассматриваемого численного метода, алгоритма и комплекса программ.
Приводится информация о численном моделировании нестационарных упругих плоских волн напряжений в упругой полуплоскости.
Для оценки физической достоверности и математической точности применяется численное моделирование. На основе метода конечных элементов в перемещениях разработаны методика, алгоритм и комплекс программ для решения линейных двумерных плоских задач динамической теории упругости. Основные соотношения метода конечных элементов получены с помощью принципа возможных перемещений. Задачи решаются методом сквозного счета, без выделения разрывов. Исследуемая область по пространственным переменным разбивается на треугольные конечные элементы с тремя узловыми точками с линейной аппроксимацией упругих перемещений и на прямоугольные конечные элементы с четырьмя узловыми точками с билинейной аппроксимацией упругих перемещений. По временной переменной исследуемая область разбивается на линейные конечные элементы с двумя узловыми точками с линейной аппроксимацией упругих перемещений. За основные неизвестные в узле конечного элемента приняты два перемещения и две скорости перемещений. Задача с начальными условиями с помощью конечноэлементного варианта метода Галеркина приведена к явной двухслойной схеме.
Рассмотрим задачу о воздействии плоской продольной волны в виде функции Хевисайда (рис. 2) на упругую полуплоскость (рис. 1).
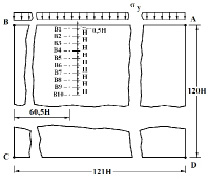
Рис. 1. Постановка задачи о распространении плоских продольных нестационарных упругих волн в полуплоскости
На границе полуплоскости AB приложено нормальное напряжение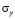 
, которое при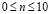 
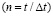изменяется линейно от 0 до P, а при 
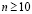равно P (
, 
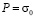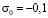МПа (–1 кгс/см2)). Граничные условия для контура BCDA при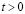 
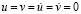. Отраженные волны от контура BCDA не доходят до исследуемых точек при 
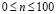. Расчеты проведены при следующих исходных данных: 
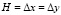; Dt=1,393•10–6 с; E=3,15•104 МПа (3,15•105 кгс/см2); 
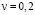; r=0,255•104 кг/м3 (0,255•10–5 кгс•с2/см4); Cp= 3587 м/с; Cs=2269 м/с. Решается система уравнений из 59048 неизвестных.
На рис. 3–12 представлено изменение нормального напряжения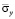 
(
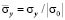) во времени n в точках B1–B10: 1 – численное решение; 2 – аналитическое решение.
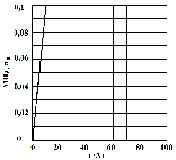
Рис. 2. Воздействие типа функции Хевисайда
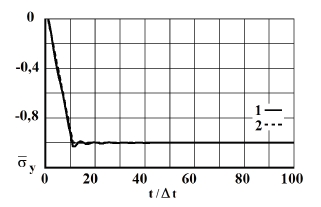
Рис. 3. Изменение упругого нормального напряжения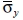 
во времени 
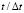в точке В1: 1 – численное решение; 2 – аналитическое решение
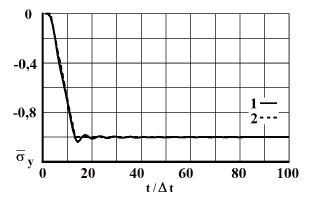
Рис. 4. Изменение упругого нормального напряжения 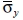во времени 
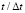в точке В2: 1 – численное решение; 2 – аналитическое решение
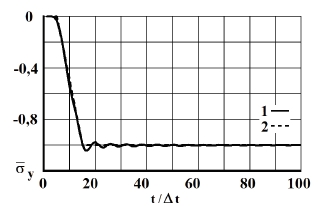
Рис. 5. Изменение упругого нормального напряжения 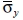во времени 
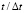в точке В3: 1 – численное решение; 2 – аналитическое решение
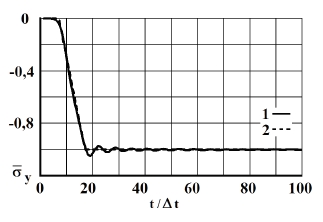
Рис. 6. Изменение упругого нормального напряжения во времени 
в точке В4: 1 – численное решение; 2 – аналитическое решение
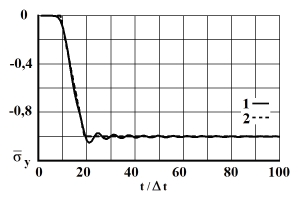
Рис. 7. Изменение упругого нормального напряжения 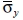во времени 
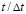в точке В5: 1 – численное решение; 2 – аналитическое решение
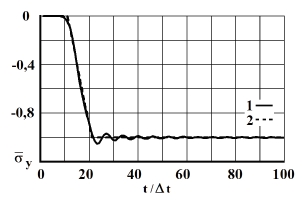
Рис. 8. Изменение упругого нормального напряжения 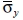во времени 
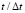в точке В6: 1 – численное решение; 2 – аналитическое решение
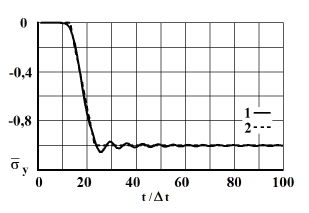
Рис. 9. Изменение упругого нормального напряжения 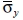во времени 
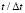в точке В7: 1 – численное решение; 2 – аналитическое решение
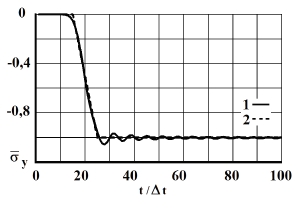
Рис. 10. Изменение упругого нормального напряжения во времени 
в точке В8: 1 – численное решение; 2 – аналитическое решение
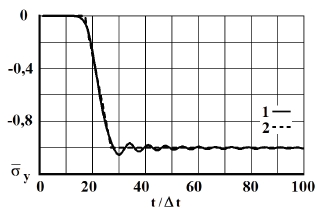
Рис. 11. Изменение упругого нормального напряжения 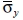во времени 
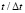в точке В9: 1 – численное решение; 2 – аналитическое решение
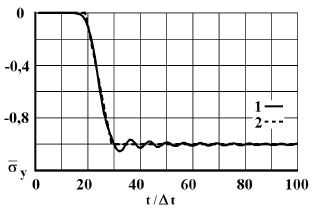
Рис. 12. Изменение упругого нормального напряжения 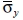во времени 
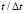в точке В10: 1 – численное решение; 2 – аналитическое решение
На фронте плоской продольной волны имеется следующая аналитическая зависимость для плоского напряженного состояния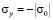 
. Отсюда видим, что точное решение задачи соответствует воздействию 
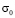(рис. 2). Для нормального напряжения 
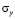имеется хорошее качественное и количественное совпадение с результатом аналитического решения. На основании проведенных исследований можно сделать вывод о физической достоверности результатов численного решения задач при распространении нестационарных упругих волн в деформируемых телах. Сравнение результатов нормальных напряжений, полученных с помощью метода конечных элементов в перемещениях, при решении задачи о распространении плоских продольных нестационарных упругих волн в полуплоскости с результатами аналитического решения, показало хорошее совпадение.