Постановки, численные методы, технология программных комплексов и анализ результатов решения нестационарных динамических задач с помощью рассматриваемого численного метода, алгоритма и комплекса программ рассмотрены в следующих работах [1–10].
В работах [3–6] приведена информация о физической достоверности и математической точности рассматриваемого численного метода, алгоритма и комплекса программ.
Для решения двумерной плоской динамической задачи теории упругости с начальными и граничными условиями используем метод конечных элементов в перемещениях. Задача решается методом сквозного счета, без выделения разрывов.
Основные соотношения метода конечных элементов получены с помощью принципа возможных перемещений. Чтобы выполнить динамический расчет методом конечных элементов, нужно иметь матрицу жесткости и матрицу инерции конечного элемента.
Принимая во внимание определение матрицы жесткости, вектора инерции и вектора внешних сил для тела Г, записываем приближенное значение уравнения движения в теории упругости
, 
, 
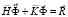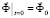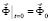, (1)
где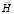 
– диагональная матрица инерции; 
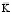– матрица жесткости; 
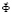– вектор узловых упругих перемещений; 
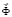– вектор узловых упругих скоростей перемещений; 
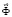– вектор узловых упругих ускорений; 
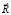– вектор внешних узловых упругих сил.
Соотношение (1) система линейных обыкновенных дифференциальных уравнений второго порядка в перемещениях с начальными условиями.
Таким образом, с помощью метода конечных элементов в перемещениях, линейную задачу с начальными и граничными условиями привели к линейной задаче Коши (1).
Интегрируя по временной координате соотношение (1) с помощью конечноэлементного варианта метода Галеркина, получим двумерную явную двухслойную конечноэлементную линейную схему в перемещениях для внутренних и граничных узловых точек
,
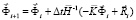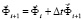, (2)
где Δt – шаг по временной координате.
Основные соотношения метода конечных элементов в перемещениях получены с помощью принципа возможных перемещений и конечноэлементного варианта метода Галеркина.
Общая теория численных уравнений математической физики требует для этого наложение определенных условий на отношение шагов по временной координате Δt и по пространственным координатам, а именно
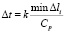
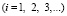, (3)
где Δl – длина стороны конечного элемента.
Устойчивость явной двухслойной схемы исследуем с помощью численного эксперимента. Результаты численного эксперимента показали, что при k = 0,5 обеспечивается устойчивость явной двухслойной схемы.
На основе метода конечных элементов в перемещениях разработаны алгоритм и комплекс программ для решения линейных плоских двумерных задач, которые позволяют решать сложные задачи при нестационарных волновых воздействиях на уникальные объекты. При разработке комплекса программ использовался алгоритмический язык Фортран-90.
Исследуемая область разбивается по пространственным переменным на треугольные конечные элементы с тремя узловыми точками с линейной аппроксимацией упругих перемещений и на прямоугольные конечные элементы с четырьмя узловыми точками с билинейной аппроксимацией упругих перемещений.
По временной переменной исследуемая область разбивается на линейные конечные элементы с двумя узловыми точками с линейной аппроксимацией упругих перемещений. Предложен квазирегулярный подход к решению системы линейных обыкновенных дифференциальных уравнений второго порядка в перемещениях с начальными условиями и к аппроксимации исследуемой области. Методика основывается на схемах: точка, линия, плоскость.
Расчеты проводились при следующих единицах измерения: килограмм-сила (кгс); сантиметр (см); секунда (с). Для перехода в другие единицы измерения были приняты следующие допущения: 1 кгс/см2 ≈ 0,1 МПа; 1 кгс с2/см4 ≈ 109 кг/м3.
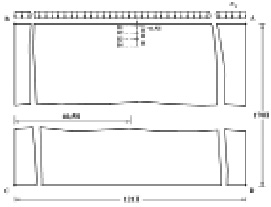
Рис. 1. Постановка задачи о распространении плоских продольных нестационарных упругих волн в полуплоскости
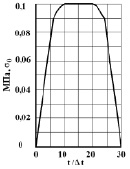
Рис. 2. Воздействие в виде прямоугольного импульса
Приводится информация о численном моделировании нестационарных упругих плоских волн напряжений в упругой полуплоскости. Для решения поставленной задачи применяем метод конечных элементов в перемещениях.
Рассмотрим задачу о воздействии плоской продольной волны в виде прямоугольного импульса (рис. 2) на упругую полуплоскость (рис. 1). На границе полуплоскости AB приложено нормальное напряжение σy, которое при 0 ≤ n ≤ 10 (n = t/Δt) изменяется от 0 до P, при 10 ≤ n ≤ 20 равно P и при 20 ≤ n ≤ 30 изменяется от P до 0 (P = σ0, σ0 = – 0,1 МПа (– 1 кгс/см2)). Граничные условия для контура BCDA при t > 0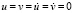 
. Отраженные волны от контура BCDA не доходят до исследуемых точек при 0 ≤ n ≤ 100. Расчеты проведены при следующих исходных данных: H = Δx = Δy; Δt = 0,125×10-4 с; E = 22,366×101 МПа (22,366×102 кгс/см2); ν = 0,22; ρ = 1,469×103 кг/м3 (1,469×10-6 кгс с2/см4); Cp = 400 м/с; Cs = 250 м/с. Решается система уравнений из 83448 неизвестных.
На рис. 3–6 представлено изменение нормального напряжения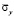 
(
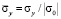) во времени n в точках B1–B4: 1 – численное решение; 2 – аналитическое решение.
Предположим, что от некоторых точек упругой среды производится какое-то возмущение. Тогда из этих точек во все стороны начинают излучаться волны. На некотором расстоянии от центра возмущения рассматриваемые волны можно представить как плоские. Тогда все частицы движутся параллельно направлению распространения волны. На фронте плоской продольной волны имеется следующая аналитическая зависимость для плоского напряженного состояния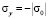 
. Отсюда видим, что точное решение задачи соответствует воздействию σ0 (рис. 2).
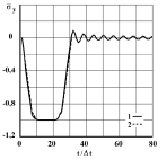
Рис. 3. Изменение упругого нормального напряжения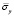 
во времени t/Δt в точке B1: 1 – численное решение; 2 – аналитическое решение
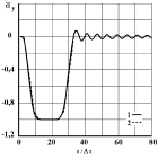
Рис. 4. Изменение упругого нормального напряжения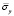 
во времени t/Δt в точке B2: 1 – численное решение; 2 – аналитическое решение
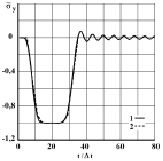
Рис. 5. Изменение упругого нормального напряжения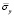 
во времени t/Δt в точке B3: 1 – численное решение; 2 – аналитическое решение
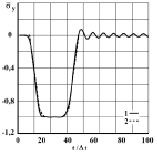
Рис. 6. Изменение упругого нормального напряжения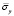 
во времени t/Δt в точке B4: 1 – численное решение; 2 – аналитическое решение
Для нормального напряжения σy имеется хорошее качественное и количественное совпадение с результатом аналитического решения. На основании проведенных исследований можно сделать вывод о физической достоверности результатов численного решения задач при распространении нестационарных упругих волн в деформируемых телах.
Сравнение результатов нормальных напряжений, полученных с помощью метода конечных элементов в перемещениях, при решении задачи о распространении плоских продольных нестационарных упругих волн в полуплоскости с результатами аналитического решения, показало хорошее совпадение.