В настоящее время вопросам безопасности окружающей среды от ударных воздействий (выбросе) нефти в водную, нефтяную и твердую деформируемую среды уделяется большое внимание. Применение моделей и методов волновой теории упругости позволит реализовать поставленную проблему.
Поставленная задача реализуется с помощью численного метода, алгоритма и комплекса программ Мусаева В.К. [1–10].
Постановка нестационарной волновой задачи
Рассмотрим задачу о нестационарном волновом воздействии на сооружение, которое находится в воздушной и твердой деформируемой среде.
Рассмотрим некоторое тело, состоящее из трех разных областей Г(1) (водная среда), Г(2) (нефтяная среда) и Г(3) (твердая среда) (рис. 1) в прямоугольной декартовой системе координат XOY, которому в начальный момент времени t=0 сообщается механическое воздействие.
Предположим, что тело Г(1) изготовлено из деформируемой водной среды и является однородным изотропным материалом, подчиняющегося упругому закону Гука при малых упругих деформациях. Если в деформируемом твердом теле предположим, что поперечная скорость распространения равна нулю, то можно получить уравнения состояния для водной среды.
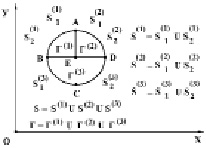
Рис. 1. Некоторое тело, состоящее из трех разных областей Г(1), Г(2) и Г(3) в прямоугольной декартовой системе координат XOY
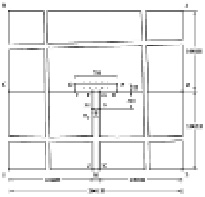
Рис. 2. Постановка задачи об ударном аварийном выбросе нефти в сложной деформируемой системе с саркофагом (плита: соотношение высоты к ширине один к семи)
Точные уравнения двумерной плоской динамической теории упругости для области Г(1) имеют вид
, 
,
,
,
,
, 
,
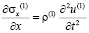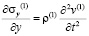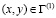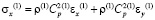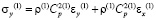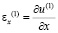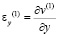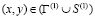, (1)
где 
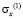и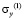 
– компоненты тензора упругих напряжени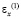й; 
и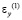 
– компоненты тензора упругих деформаци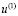й; 
и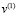 
– составляющие вектора упругих перемещений вдоль осей OX и OY соответственно; 
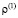– плотность материала; 
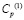– скорость продольной упругой волны; 
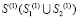– граничный контур тела Г(1).
Систему (1) в области, занимаемой телом Г(1), следует интегрировать при начальных и граничных условиях.
Предположим, что тело Г(2) изготовлено из деформируемой нефтяной среды и является однородным изотропным материалом, подчиняющегося упругому закону Гука при малых упругих деформациях. Если в деформируемом твердом теле предположим, что поперечная скорость распространения равна нулю, то можно получить уравнения состояния для нефтяной среды.
Точные уравнения двумерной плоской динамической теории упругости для области Г(2) имеют вид
, 
,
,
,
,
, 
,
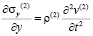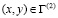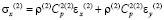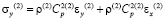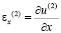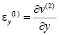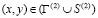, (2)
где 
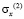и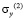 
– компоненты тензора упругих напряжени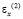й; 
и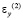 
– компоненты тензора упругих деформаций; u(2) и v(2) – составляющие вектора упругих перемещений вдоль осей OX и OY соответственно; 
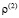– плотность материала; 
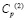– скорость продольной упругой волны; 
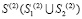– граничный контур тела Г(2).
Систему (2) в области, занимаемой телом Г(2), следует интегрировать при начальных и граничных условиях.
Точные уравнения двумерной плоской динамической теории упругости для области Г(3) (твердая среда) имеют вид
,
,
,
,
,
,
, 
,
,
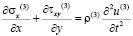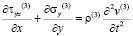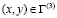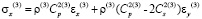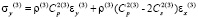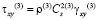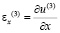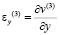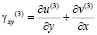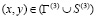, (3)
где 
, 
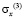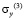и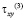 
– компоненты тензора упругих напряжени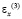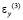й; 
, 
и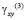 
– компоненты тензора упругих деформаций; u(3) и v(2) – составляющие вектора упругих перемещений вдоль осей OX и OY соответственно; 
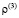– плотность материала; 
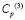– скорость продольной упругой волны; 
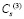– скорость поперечной упругой волны; 
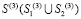– граничный контур тела Г(3).
Систему (3) в области, занимаемой телом Г(3), следует интегрировать при начальных и граничных условиях.
В работах [1, 3–6] приведена информация о верификации (оценка достоверности и точности) применяемого численного метода, алгоритма и комплекса программ.
Постановка задачи об ударном аварийном выбросе нефти
Расчеты проводились при следующих единицах измерения: килограмм-сила (кгс); сантиметр (см); секунда (с). Для перехода в другие единицы измерения были приняты следующие допущения: 1 кгс/см2 ≈ 0,098 МПа; 1 кгс с2/см4 ≈ 0,98*109 кг/м3.
Для твердой деформируемой среды приняты следующие исходные данные: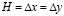 
; Δt = 1,393*10–6 с; E = 3,09*10 4 МПа (3,15*10 5 кгс/см2); n= 0,2; r= 0,25*104 кг/м3 (0,255*10–5 кгс с2/см4); Cp = 3587 м/с; Cs = 2269 м/с. Для водной деформируемой среды приняты следующие исходные данные: 
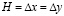; Δt = 3,268*10–6 с; r = 1,025*103 кг/м3 (1,045*10 -6 кгс с2/см4); Cp= 1530 м/с. Для нефтяной деформируемой среды приняты следующих исходные данные: 
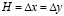; Δt = 3,876*10–5 с; r = 0,825*103 кг/м3 (0,841*10–6 кгс с2/см4); Cp= 1290 м/с.
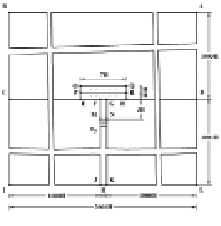
Рис. 3. Постановка задачи об ударном аварийном выбросе нефти в сложной деформируемой системе с саркофагом (плита: соотношение высоты к ширине два к семи)
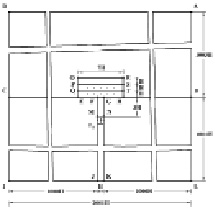
Рис. 4. Постановка задачи об ударном аварийном выбросе нефти в сложной деформируемой системе с саркофагом (плита: соотношение высоты к ширине три к семи)
Рассмотрим задачу об ударном аварийном выбросе нефти в сложной системе, которая состоит из разных деформируемых сред (водной, нефтяной и твердой), а так же из твердого деформируемого саркофага (соотношение высоты к ширине один к семи) (рис. 2). На контуре MN приложено нормальное воздействие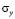 
, которое при 
(
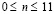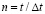) изменяется линейно от 0 до P, при 
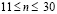равно P и при 
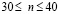от P до 0 (
, 
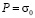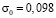МПа (1 кгс/см2)). Граничные условия для контура ABCILD при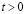 
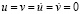. Отраженные волны от контура ABCILD не доходят до исследуемых точек при 
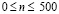. Твердые деформируемые среды FECIJM, DHGNKL и POEFGH. Водная деформируемая среда ABCEOPHD. Нефтяная деформируемая среда GFMJKN. На границе материалов с разными свойствами приняты условия непрерывности перемещений. При расчетах принимается минимальный шаг по времени Δt = 1,393*10–6 с. Исследуемая расчетная область имеет 4014010 узловых точек. Решается система уравнений из 16056040 неизвестных.
Рассмотрим задачу об ударном аварийном выбросе нефти в сложной системе, которая состоит из разных деформируемых сред (водной, нефтяной и твердой), а так же из твердого деформируемого саркофага (соотношение высоты к ширине два к семи) (рис. 3). На контуре MN приложено нормальное воздействие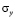 
, которое при 
(
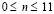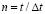) изменяется линейно от 0 до P, при 
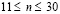равно P и при 
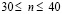от P до 0 (
, 
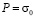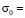0,098 МПа (1 кгс/см2)). Граничные условия для контура ABCILD при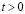 
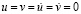. Отраженные волны от контура ABCILD не доходят до исследуемых точек при 
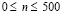. Твердые деформируемые среды FECIJM, DHGNKL и QOPEFGHR. Водная деформируемая среда ABCEPOQRHD. Нефтяная деформируемая среда GFMJKN. На границе материалов с разными свойствами приняты условия непрерывности перемещений. При расчетах принимается минимальный шаг по времени Δt = 1,393*10–6 с. Исследуемая расчетная область имеет 4014010 узловых точек. Решается система уравнений из 16056040 неизвестных.
Рассмотрим задачу об ударном аварийном выбросе нефти в сложной системе, которая состоит из разных деформируемых сред (водной, нефтяной и твердой), а так же из твердого деформируемого саркофага (соотношение высоты к ширине три к семи) (рис. 4). На контуре MN приложено нормальное воздействие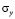 
, которое при 
(
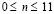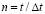) изменяется линейно от 0 до P, при 
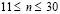равно P и при 
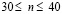от P до 0 (
, 
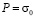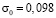МПа (1 кгс/см2)). Граничные условия для контура ABCILD при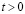 
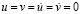. Отраженные волны от контура ABCILD не доходят до исследуемых точек при 
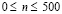. Твердые деформируемые среды FECIJM, DHGNKL и ROPQEFGHTS. Водная деформируемая среда ABCEQPORSTHD. Нефтяная деформируемая среда GFMJKN. При расчетах принимается минимальный шаг по времени Δt = 1,393*10–6 с. На границе материалов с разными свойствами приняты условия непрерывности перемещений. Исследуемая расчетная область имеет 4014010 узловых точек. Решается система уравнений из 16056040 неизвестных.
Результаты расчетов были получены для нормального напряжения
,
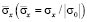для нормального напряжения
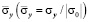
и для касательного напряжения
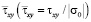
во времени n в точках B1–B10, которые показаны на рис. 2–4 и на рис. 5.
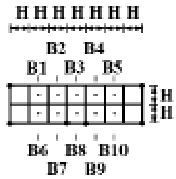
Рис. 5. Точки B1–B10, в которых получены компоненты тензора напряжений
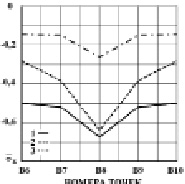
Рис. 6. Изменение максимальных сжимающих величин упругого нормального напряжения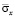 
в точках B6–B10 в задачах с саркофагом: 1 – плита: соотношение высоты к ширине один к семи; 2 – плита: соотношение высоты к ширине два к семи; плита: 3 – соотношение высоты к ширине три к семи
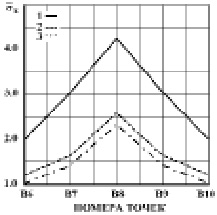
Рис. 7. Изменение максимальных растягивающих величин упругого нормального напряжения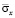 
в точках B6–B10 в задачах с саркофагом: 1 – плита: соотношение высоты к ширине один к семи; 2 – плита: соотношение высоты к ширине два к семи; плита: 3 – плита: соотношение высоты к ширине три к семи
На рис. 6 показано изменение максимальных сжимающих величин упругого нормального напряжения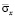 
в точках B6–B10 в задачах с саркофагом: 1 – плита: соотношение высоты к ширине один к семи; 2 – плита: соотношение высоты к ширине два к семи; плита: 3 – соотношение высоты к ширине три к семи.
На рис. 7 показано изменение максимальных растягивающих величин упругого нормального напряжения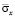 
в точках B6–B10 в задачах с саркофагом: 1 – плита: соотношение высоты к ширине один к семи; 2 – плита: соотношение высоты к ширине два к семи; плита: 3 – соотношение высоты к ширине три к семи.