Данная работа является дополнительным материалом к курсу «Гидромеханика» при изучении вопроса о турбулентном движении жидкости.
Постановка задачи
Рассмотрим плоское стационарное турбулентное движение тяжёлой вязкой жидкости по горизонтальной плоскости при наличии свободной поверхности с учётом влияния вязкого подслоя.
Аналогичная задача для турбулентного потока тяжёлой жидкости по наклонной плоскости без учёта влияния вязкого подслоя рассмотрена в работе [1].
С учетом всех допущений, предположений и выводов, сделанных в [1], получаем следующую краевую задачу:
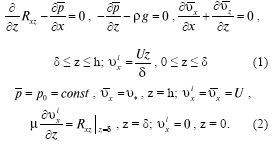
Здесь функция Rxz - добавочное напряжение Рейнольдса [2], р‾ - осредненное гидродинамическое давление, υ‾х - среднее значение горизонтальной скорости турбулентного потока, р - плотность жидкости, g - ускорение свободного падения, μ- коэффициент внутреннего трения (коэффициент вязкости), μ = pv, v - кинематический коэффициент вязкости, δ - толщина ламинарного подслоя. Начало координат выбрано на неподвижной горизонтальной плоскости Оху. Ось Оу - горизонтальна, ось Oz направлена перпендикулярно к плоскости вверх, ось Ох лежит в горизонтальной плоскости и направлена по направлению потока. Из всех массовых сил действует только сила тяжести: Fx = 0, Fz = -g. Согласно [2] имеем:
![]()
Считаем, что турбулентное движение жидкости в среднем происходит в направлении оси Ох и, что средняя скорость этого плоского движения существенным образом зависит лишь от координаты z: υ‾х =υ‾х (z).
Считаем, что сверху поток ограничен свободной поверхностью, на которой выполняется динамическое условие равенства нормального напряжения в жидкости атмосферному давлению p0=const. Касательное напряжение на свободной поверхности тождественно равно нулю, так как турбулентный поток рассматривается без учёта внутреннего трения (и=0). Кинематическое условие на свободной поверхности выполняется автоматически, так как мы полагаем υ‾z = 0.
Введём ещё в рассмотрение расход жидкости Q через поперечное сечение потока:
![]()
Решение задачи (1)-(3)
Из второго уравнения в (1) с учетом первого условия в (2) находим.
![]()
Подставляя (5) в первое уравнение в (1) с учётом (3), выводим:
![]()
Здесь т0 - добавочное напряжение на границе ламинарного пограничного слоя (вязкого подслоя).
Из (3), (6) находим:
![]()
Считая кривизну функции υ‾x (z) положительной, в (7) выбираем знак плюс.
Интегрируя (7), получаем представление для υ‾.x:
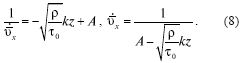
Здесь А - постоянная, подлежащая определению.
Интегрируя (8), находим υ‾x:
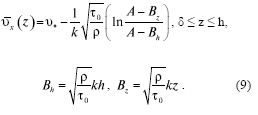
Введём теперь в рассмотрение ламинарный подслой толщины 5, в котором необходимо учитывать и вязкое трение. В ламинарном подслое скорость υx =υix меняется по линейному закону [2]:
![]()
Здесь U- скорость потока на границе подслоя. Скорость U находится из (9) при z = 5. Тогда
![]()
Согласно интегральному соотношению Кармана [2] имеем:
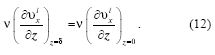
То есть, добавочное напряжение т0, участвующее в (6)-(9) совпадает со значением трения в вязком подслое на самой стенке. Далее, будем считать, что на границе вязкого подслоя «сшиваются» не только скорости, но и их первые производные.
Таким образом, согласно (10) и (12), имеем уравнения:

Два уравнения в (13) связывают три величины А, т0 и δ.
В настоящее время существуют приборы, позволяющие определять касательные напряжения на поверхностях, по которым движется вязкая жидкость [3]. Поэтому в уравнениях (13) касательное напряжение на дне т0 можно считать известным. Тогда из первого уравнения в (13) находится А. Из второго уравнения (13) определяется 5 по итерационному процессу, который сходится при значениях δ / h много меньших единицы:
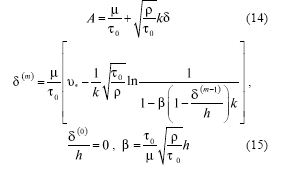
Подставляя (15) в (14), а затем найденное выражение для А в (9), выводим:
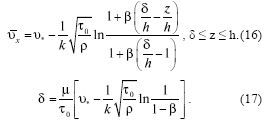
Вычислим теперь расход Q по формуле (4):
![]()
Учитывая (8), находим:
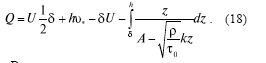
Вычисляя интеграл, выводим
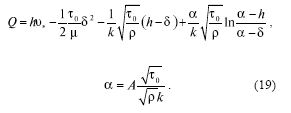
Формулы (5), (9), (10), (13), (16), (17) и (19) дают решение задачи о турбулентном движении вязкой жидкости по горизонтальному дну при наличии свободной поверхности с учётом вязкого подслоя.
Если касательное напряжение т0 на дне неизвестно, но известен расход Q, то равенство (19), с учётом формул (14) и (17) представляет собой уравнение для т которое должно быть решено численно. При значениях β много меньших единицы выведены асимптотические представления для δ, т0, u¯х и uiх.
Список литературы
- Потетюнко Э.Н. Турбулентный поток жидкости по наклонной плоскости // Успехи современного естествознания. - 2010. - №9. - с. 224-226.
- Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая гидромеханика. М.: Физматгиз, 1963.
- Рябинин А.Н. Моделирование пограничного слоя вблизи морского дна с переносимыми твёрдыми частицами // Труды X Всероссийской конференции «Прикладные технологии гидроакустики и гидрофизики». - СПб.: Наука, 2010.- С. 264-266.

