В общем понимании беспилотный летательный аппарат (БПЛА) – это летательный аппарат без экипажа на борту. Различают беспилотные летательные аппараты: неуправляемые; автоматические; беспилотные дистанционно-пилотируемые летательные аппараты. А также БПЛА принято делить по таким взаимосвязанным параметрам, как масса, время, дальность и высота полёта.
Преимущества БПЛА в том, что имеется возможность использования различных сочетаний высот и скоростей полета: основную часть траектории аппарат летит на большой высоте при малом аэродинамическом сопротивлении, а перед целью выходит на малую высоту с максимально возможной скоростью полета, что затрудняет перехват. Предусмотрена также возможность маневра на любом участке траектории.
В качестве силовой установки (СУ) применяются короткоресурсные или прямоточные воздушно-реактивные двигатели. Системы автоматического управления (САУ) СУ были спроектированы как самые простые, в классе односвязных САУ, их техническая реализация – электронно-гидравлическая с резервными гидромеханическими каналами. При синтезе алгоритмов управления учитывались только изменения режимов работы и условий применения СУ, динамика агрегатов дозирования топлива (АДТ) не учитывались. Тем не менее, практический опыт и результаты натурных и стендовых испытаний показали, что динамические процессы в системе топливопитания оказывают значительное влияние на динамику СУ. Автономные исследования агрегатов топливопитания на полунатурных стендах подтвердили, что переходные процессы в гидроавтоматике по времени соразмеримы с динамическими процессами в СУ для БПЛА, в отличие от транспортных или пассажирских летательных аппаратов (ЛА) [1]. Тем самым подтверждается актуальность выбранной темы.
Анализ результатов натурных испытаний позволил сделать вывод, что чаще всего проявлялись следующие недостатки в работе СУ, связанные с функционированием САУ: появление автоколебательных режимов на отдельных участках траектории полета, что недопустимо по условиям эксплуатации любого ЛА; отказы агрегатов топливопитания, связанные с изменением физических свойств топлива (перегревом, кавитацией и т.п.) в процессе эксплуатации изделия.
Появление новых типов ЛА и двигателей для них, введение в контуры управления высокоточных вычислительных машин поставило перед разработчиками систем управления следующую проблему: характеристики управляющей (электронной) и исполнительной (гидромеханической) частей системы должны быть согласованы или хотя бы не противоречить друг другу. При этом в развитии методов проектирования и методов исследования исполнительных гидромеханических механизмов наблюдалось заметное отставание [3].
Целью работы является обоснование нового подхода к проектированию САУ СУ БПЛА, основанного на введении математических моделей СУ и агрегата топливопитания в контур управления частотой вращения ротора турбокомпрессора, при этом алгоритм управления корректируется по комплексу получаемых ошибок, как по расходу топлива, так и по частоте вращения.
Для устранения недостатков в работе САУ предлагается решить следующие задачи:
• разработать математические модели объекта управления, способные адекватно отображать поведение объекта при изменении режима работы и условий применения;
• разработать математические модели АДТ с учетом их конструктивных особенностей и изменения физических свойств рабочей жидкости;
• разработать методы анализа и синтеза САУ предложенного типа.
Рассмотрим последовательно методологию решения каждой из поставленных задач.
Методы решения
Математические модели объекта управления
Математическая модель объекта управления – СУ – представляется в виде динамических уравнений, которые записываются в дифференциальной, интегральной и разностной формах [3].
Существующие типы математических моделей силовых установок можно разделить на следующие виды: полная нелинейная модель; линейная математическая модель в физических переменных; кусочно-линейная модель; быстросчетная динамическая модель с переменными коэффициентами; динамическая модель на базе динамической характеристики (расчетной или экспериментальной) СУ; нейросетевая модель.
Каждая из вышеперечисленных моделей обладает как своими достоинствами, так и конкретными недостатками. Не перечисляя их, отметим тот факт, что для проектирования САУ необходимы только динамические нелинейные модели СУ. В основу таких моделей положена динамическая характеристика (ДХ) СУ, которую получают или расчетным (с помощью полноразмерной модели), или экспериментальным путем.
Как объект управления СУ можно охарактеризовать передаточным звеном, у которого входной координатой является расход топлива (GT), а выходной – частота вращения ротора турбокомпрессора (n), при этом температура газа, давление воздуха за компрессором и другие величины рассматриваются как контролируемые параметры (рис. 1а).
Именно такой подход используется в настоящее время на профильных предприятиях, при этом синтез алгоритмов управления производится для заданной расчетной точки, а на других режимах лишь проверяется качество управления по заранее заданным критериям.
Предлагается использовать новый подход к построению динамической модели СУ для БПЛА. При моделировании предполагается, что динамические кривые будут представлены в виде совокупности трех взаимосвязанных матриц: по частоте вращения ротора турбокомпрессора, по расходу топлива, по ускорению ротора турбокомпрессора.
В зависимости от режима работы и условий применения выбираться та или иная матрица, расчет проводится как в физических, так и в приведенных параметрах. Матрица по расходу топлива представляет собой составную матрицу вида
.
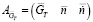Взяв определённое значение относительного расхода топлива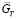 
, которое принимается за константу, в матрицу заносятся значения 
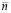и 
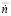, полученные в точках пересечения прямой с кривыми линиями динамической характеристики (рис. 1б). Этот процесс повторяется многократно зависимости от выбранной точности расчета. Аналогично составляются две другие матрицы по ускорению ротора 
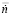и по частоте вращения 
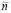турбокомпрессора. Они имеют вид
и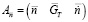 
соответственно. Таким образом, обеспечивается плавный переход с режима на режим работы СУ, начиная с режима запуска и до выхода на режим стабилизации, а введение как физических, так и приведенных параметров позволяет моделировать и условия эксплуатации СУ. Данный подход положен в основу математической модели СУ для БПЛА.
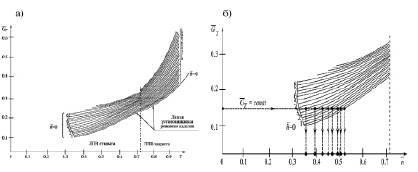
Рис. 1: а – динамическая характеристика силовой установки БПЛА: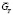 
– относительное значение расхода топлива, 
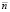– относительная частота вращения ротора, 
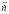– относительное ускорение ротора; б – матрица значений по расходу топлива (
)
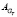Математические модели исполнительных механизмов
Обычно при моделировании агрегата дозирования топлива (АДТ) использовалась нелинейная система дифференциальных уравнений, описывающих баланс сил на сервопоршне дроссельной иглы как основном элементе АДТ, а также баланс расходов в проточных полостях подвижных элементов. Такой подход позволял получить передаточную функцию элемента в виде апериодического или колебательного звена. При изменении режима работы элемента его параметры менялись, что снижало качество управления двигателем и требовало изменения алгоритмов управления.
Подобный метод дает приближенный результат, не поддается формализации и, следовательно, не может быть автоматизирован. Кроме того, в процессе получения математической формулы теряется связь с реальной конструкцией АДТ. Поэтому значительный интерес представляет сетевой метод расчета АДТ, позволяющий производить расчеты посредством матричных операций, которые относительно легко формализуются и довольно просты в машинной реализации, тем более что матричный метод используется и для моделирования объекта управления – двигателя [4].
Суть метода в том, что принципиальная (конструкторская) схема АДТ заменяется ориентированным графом, то есть сохраняется связь между реальной конструкцией и математическим описанием. Метод хорошо зарекомендовал себя для расчета статических характеристик АДТ как элемента САУ СУ, но динамику просчитать достаточно сложно в силу того, что перемещение любого элемента (поршня) приводит к изменению динамических составляющих потоков жидкости, перетекающих из одной полости в другую.
Для получения динамической модели АДТ предложено использовать следующий подход: во-первых, движение подвижных элементов описывать с помощью уравнения Ньютона; во-вторых, движение потоков жидкости (топлива) описывать с помощью уравнения Навье-Стокса).
Таким образом, учитываются динамические параметры агрегата с учетом его конструкторских особенностей, а также физико-механических свойств жидкости (температуры, вязкости, плотности и т.д.).
Приведем основные результаты, полученные ранее, для достаточно подробной аргументации предлагаемого подхода. Показаны зависимость координаты положения поршня от времени для различных значений силы трения F0 (рис. 2а) и зависимость установившейся амплитуды колебаний поршня от силы трения (рис. 2б).
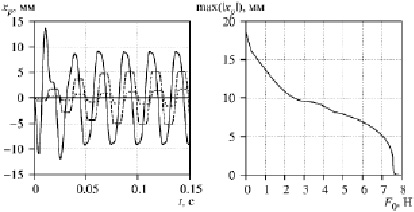
Рис. 2. Зависимость координаты поршня при F0 = 1 Н (сплошная линия), F0 = 7 Н (штриховая линия), F0 = 7.5 Н (пунктирная линия) (а) и силы трения (б) от времени
Заметим, что в процессе работы агрегата возможно появление различных параметрических неопределенностей, в том числе появление так называемой «метелки» – расслоения статических характеристик, что в принципе недопустимо (рис. 3).
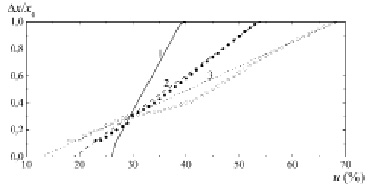
Рис. 3. Отклонение сервопоршня от начального положения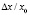 
в зависимости от управляющего сигнала u для различных значений жиклеров sвх,i / α, sсл,i / α (i = 1, 2): 1 – a = 1; 2 – a = 2.5, 3 – a = 4, п, полученные при численных расчетах (линии) и экспериментально (круги)
Полученные результаты позволяют сделать вывод, что динамические процессы в элементах топливной автоматики должны учитываться при синтезе алгоритмов системы управления, но при этом необходимо отделить динамические процессы в СУ от динамических процессов в АДТ, поскольку они соразмеримы по времени.
Структура электронно-гидравлической САУ СУ БПЛА
САУ СУ БПЛА целесообразно проектировать в классе адаптивных или интеллектуальных САУ, но при этом следует учитывать, что динамические процессы, протекающие в короткоресурсных СУ, имеют достаточно высокую скорость (всего несколько секунд от момента розжига камеры сгорания до выхода на заданный режим). Параметры, характеризующие режимы работы двигателя и внешние условия применения БПЛА, изменяются в несколько раз в соответствии с изменениями режима работы и условий применения СУ, что требует таких же изменений динамических параметров САУ. Кроме того, как уже упоминалось ранее, динамические процессы, происходящие в агрегатах топливопитания, по своей сложности и скорости изменения не уступают процессам, протекающим в двигателе. Известные подходы к проектированию адаптивных САУ СУ описаны более подробно в [6].
Система управления, использующая обобщенный настраиваемый объект в контуре управления, обладает следующим недостатком: задача адаптации успешно решается только для стационарного линейного объекта.
Для устранения указанного недостатка, предлагается использовать следующий подход: ввести в структуру САУ многорежимные динамические модели непосредственно самой СУ и АДТ, также сформировать многоканальный адаптивный контур коррекции сигналов, в который вводятся сигналы как с реального устройства (СУ и АДТ), так и с их динамических моделей. Контур коррекции в свою очередь включает в себя логический блок (ЛБ), дифференциатор, демультиплексор, электронный регулятор и программу управления.
Структурная схема предложенной САУ СУ БПЛА приведена на рис. 4.
В многоканальный адаптивный контур коррекции поступают следующие сигналы: рассогласование между реальными и модельными характеристиками СУ и АДТ, а также рассогласование между объединенными реальными и модельными характеристиками СУ и АДТ. Как видно из схемы (рис. 4) модель СУ введена в схему дважды, в первом случае сигнал поступает от модели АДТ для того чтобы получить рассогласование между реальными АДТ, СУ и их моделями; во втором случае – сигнал поступает от реального АДТ, проходя через датчики 1, чтобы получить рассогласование между реальным СУ и его моделью.
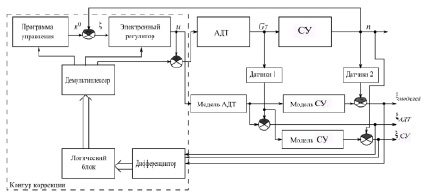
Рис. 4. Предлагаемая САУ СУ БПЛА, в которую входит АДТ, СУ, датчики 1 и датчики 2, модель АДТ, модель СУ, контур коррекции
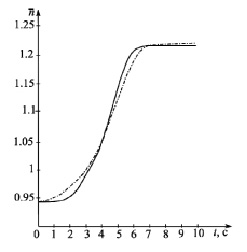
Рис. 5. Результат моделирования предложенной САУ СУ БПЛА: (– – –) полученная зависимость относительной частоты вращения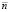 
от времени t; (–) заданная зависимость относительной частоты вращения 
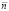от времени t
Более подробное описание работы ЛБ рассмотрено в работе [2].
Результаты. Используя известные подходы к моделированию САУ в среде MATLAB, была исследована в первом приближении система, представленная на рис. 4. Результаты моделирования САУ (рис. 5), представлены в виде зависимости относительной частоты вращения ротора турбокомпрессора от времени. Одна из них получена с помощью моделирования САУ СУ, а вторая – задана.
Полученные результаты подтверждают правомерность нового подхода к проектированию САУ СУ БПЛА, поскольку погрешность не превышает 2 % от текущего значения частоты вращения ротора турбокомпрессора по сравнению с заданной характеристикой. На разработанную структуру САУ получен патент [5].
Заключение
В статье приведено обоснование нового подхода к проектированию САУ СУ БПЛА, основанного на введении математических моделей СУ и АДТ в контур управления частотой вращения ротора турбокомпрессора, при этом алгоритм управления корректируется по комплексу получаемых ошибок, как по расходу топлива, так и по частоте вращения.