Иногда возникает необходимость измерить электрофизические параметры диэлектрических тонких образцов, а именно диэлектрической проницаемости и площади поперечного сечения лабораторными методами. Сначала получим формулы для расчета электрофизических параметров на основе метода малых возмущений, а затем проведем экспериментальные измерения параметров. Эксперимент проводился на панорамном измерителе Р2–61. Схема установки приведена на рис. 1.
Сначала измеряется резонансная частота объемного резонатора без образца, а затем с образцом и на основе смещения резонансной частоты оцениваются диаметр и диэлектрическая проницаемость тонкого образца [2]. Далее проводится моделирование аналога установки в среде Microwave Studio в диапазоне частот 7–13 ГГц [2].
1. Метод малых возмущений для расчета диаметра и диэлектрической проницаемости тонких образцов
Наиболее известным из резонаторных методов измерения является метод, при котором пропускают контролируемое изделие (провод, стержень, нити) через сквозное отверстие в полости объемного резонатора и затем измеряют его резонансную (собственную) частоту.
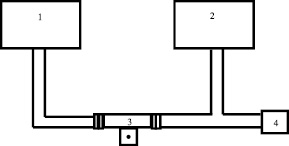
Рис. 1. Установка для измерения диэлектрической проницаемости с образцом: 1 – генератор качающейся частоты ГКЧ-61; 2 – индикатор Я2Р-67; 3 – отрезок прямоугольного волновода с резонатором; 4 – согласованная нагрузка
Таким образом, работа подобных устройств основывается на измерении резонансных частот СВЧ объемного резонатора, который содержит контролируемый объект в виде диэлектрического стержня (нити), расположенный или параллельно, или перпендикулярно силовым линиям электрического поля в резонаторе. Будем считать, что стержень занимает в резонаторе довольно малый объем V по сравнению с объемом V0 резонатора, тогда можно применить теорию возмущений, чтобы получить формулы для расчета диэлектрической проницаемости и толщины тонких стержней.
Далее будем рассматривать объемный прямоугольный резонатор, в котором возбуждены колебания типа H101, диэлектрический стержень в резонаторе расположен параллельно силовым линиям электрического поля в максимуме этого поля, как это представлено на рис. 2.
Предлагаемый далее метод малых возмущений основывается на приблизительном сравнении двух бесконечно близких стационарных состояний электромагнитного поля. Одно из этих состояний характеризуется параметрами ω, Е, Н, V, S, а другое отличается от него достаточно малым изменением первоначально установленных величин и , в этом случае, будет иметь следующие параметры ω+ω0, Е+δЕ, Н+δН, V+δV, S+δS, при этом будем предполагать, что всех рассматриваемые изменения будут иметь одинаковый порядок малости.
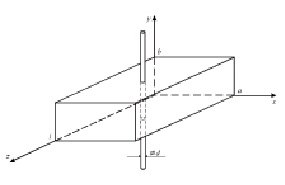
Рис. 2. Прямоугольный объемный резонатор с колебаниями типа H101 и с диэлектрическим образцом
В исходном случае электромагнитное поле в отсутствии сторонних токов описывается следующими уравнениями Максвелла:
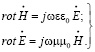(1)
Далее будем обозначать через μ и относительные магнитную и диэлектрическую проницаемость, соответственно.
Опираясь на теорему Умова-Пойнтинга для исходного поля можно записать следующее уравнение в дифференциальной форме:
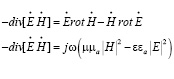(2)
Перепишем уравнение (2) в интегральной форме:
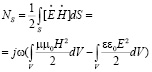(3)
Далее применим метод малых возмущений, тогда уравнения Максвелла запишутся в виде:
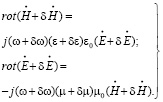(4)
Если пренебречь величинами второго порядка малости, то из уравнений (1), (2), и (3), можно получить следующую систему уравнений:
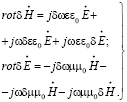(5)
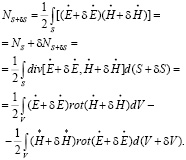
Опираясь на систему (5), можно получить следующее равенство (здесь учтено, что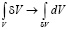 
):
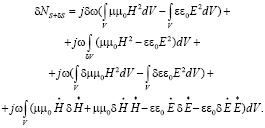(6)
Чтобы упростить уравнение (6) следует учесть несколько тождественных векторных преобразований. Так аналогично (2) и с учетом (1) и (4) можно записать следующее выражение:
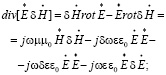
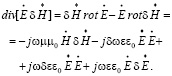
Вычтем из первого равенства второе и произведем перегруппировку, получим равенство
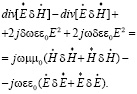(7)
Учтено, что:
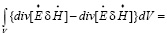
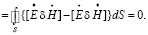(8)
Потому что вблизи поверхности металлических стенок S, ограничивающих поле в объемном резонаторе, магнитное поле имеет только касательные составляющие, а электрическое поле – только нормальные.
Так как полость резонатора ограничена проводящей поверхностью, то потоки энергии, проходящие через ее поверхность внутри объема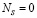 
и приращение энергии 
.
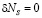В итоге, из выражения (3), получим:
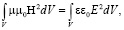(9)
из (6) и с учетом (7) и (8) получим выражение
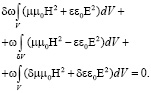(10)
Поместим в резонатор с объемом V цилиндрический стержень с поперечным сечением А и длиной b и как это показано на рис. 2. Поскольку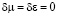 
и учтем, что m диэлектрического образца равно 1, формулу (10) можно переписать в следующем виде:
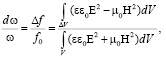(11)
где f0 – собственная резонансная частота объемного резонатора.
Диэлектрический образец помещен в максимум электрического поля E1, где в центре объемного резонатора можно записать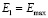 
.
Из формулы (9) можно получить, что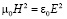 
и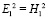 
, тогда формулу (11) перепишем в виде:
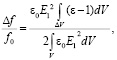(12)
Энергию поля в объемном прямоугольном резонаторе можно определить следующим выражением:
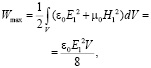
а значение в знаменателе формулы запишем в виде (12):
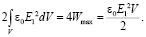
Подставим значение Wmax в (12), и тогда само выражение принимает следующий вид:
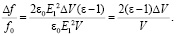
Учтем, что объем образца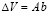 
, где А – площадь поперечного сечения образца, то предыдущее выражение примет вид:
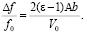(13)
Учитывая, что для цилиндрического образца диаметра d, поперечное сечение рассчитывается по формуле
,
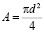а внутренний объем прямоугольного резонатора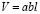 
, получим формулу для расчета диаметра цилиндрического образца:
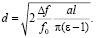(14)
Из формулы (14) можно получить формулу для расчета диэлектрической проницаемости ε при известном диаметре d:
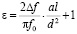. (15)
Рассмотрим цилиндрический объемный резонатор с тонким диэлектрическим образцом, который показан на рис. 3. Проводя аналогичные рассуждения, как и для прямоугольного резонатора, на основе метода малых возмущений, получим формулы для расчета диаметра (16) и диэлектрической проницаемости (17) тонкого диэлектрического образца для колебания типа Е010.
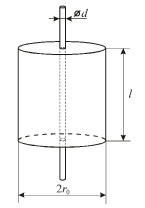
Рис. 3. Цилиндрический объемный резонатор с диэлектрическим стержнем
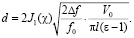(16)
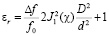, (17)
здесь d – диаметр образца; D – диаметр цилиндрического резонатора;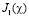 
– функция Бесселя первого рода, первого порядка.
2. Экспериментальные измерения параметров диэлектрических цилиндрических образцов
Были изготовлены макеты прямоугольного и цилиндрического резонаторов из медной фольги. По схеме рис. 1, меняя параметры (диаметр и диэлектрическую проницаемость) образца на панорамном измерителе измеряется сдвиг частоты ∆f, а затем по полученным выше формулам вычисляются либо d, либо ε. Результаты измерения (рис. 4) и расчета немного отличаются от величины ε =9.6. Но измерить ε точно, вообще трудно. А с уменьшением диаметра трудней становится измерить ∆f.
Как показывают результаты эксперимента и расчета, наибольшее расхождение между расчетными и экспериментальными данными не превышает 20 %, что приемлемо для лабораторных измерений.
Описанным выше методом по сдвигу резонансной частоты на основе цилиндрического резонатора были измерены, и по формуле (17) рассчитаны диэлектрические проницаемости трех цилиндрических образцов диаметром 2 мм: 1 – образец εr =3, измеренное значение равно 3.12; 2 – образец εr =5, измеренное значение равно 5.21; 3 – образец εr =9.6, измеренное значение равно 9.24. И в этом случае ошибка измерения не превышает 20 %.
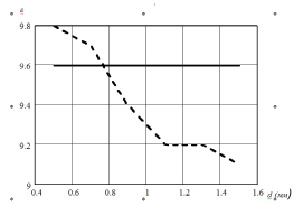
Рис. 4. Кривая диэлектрической проницаемости стержня из поликора (ε =9.6) для разных диаметров при измерении на прямоугольном резонаторе
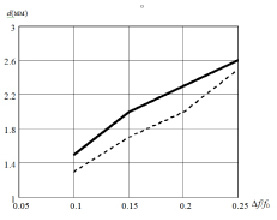
Рис. 5. Результаты измерения диаметра цилиндрического образца с εr = 9.6: здесь сплошная кривая расчетная по формуле (17); штриховая – экспериментальная, при измерении на основе цилиндрического резонатора
3. Моделирование измерения электрофизических параметров тонких диэлектрических образцов в среде Macrowave Studio
Было проведено моделирование методов измерения в среде Macrowave Studio [1]. Сначала проектировались объемные резонаторы, затем в резонатор помещался измеряемый образец и измерялся относительный сдвиг частоты (f/f0) при изменении диаметра или диэлектрической проницаемости образца. Далее рассчитываются параметры образца по формулам (14–17). Например, прямоугольный резонатор с образцом показан на рис. 6.
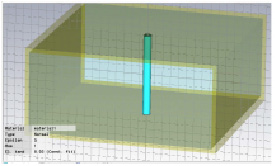
Рис. 6. Прямоугольный резонатор с образцом
Смещение частоты определялось по смещению минимума кривой элемента матрицы рассеяния S11, как показано на рис. 7. Кривые зависимости диэлектрической проницаемости εr от относительного сдвига частоты (f/f0) показаны на рис. 8.
Аналогичная кривая получена для прямоугольного резонатора. Расхождение между расчетными и смоделированными кривыми не превышает 15 %. Получены кривые зависимости диэлектрической проницаемости при разных диаметрах, например, рис. 9, а также, кривые зависимости диаметра образца при разной диэлектрической проницаемости εr.
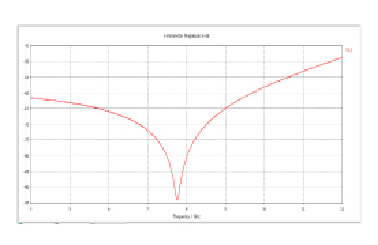
Рис. 7. Резонансный минимум кривой S11 по частоте (по оси абсцисс в ГГц) εr
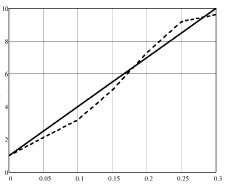
Рис. 8. Зависимость диэлектрической проницаемости от относительного сдвига частоты (сплошная линия – расчетная, штриховая – результат моделирования) для цилиндрического резонатора
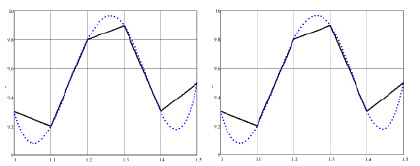
Рис. 9. Кривая диэлектрической проницаемости εr для разных диаметров стержня d мм (штриховая кривая – сглаженная, для εr =9.6)
Выводы
Результаты эксперимента и моделирования подтверждают адекватность формул метода возмущений. Таким образом, на основе объемных резонаторов можно с точностью до 15 % измерять диэлектрическую проницаемость или диаметр тонких образцов. Причем методы измерения можно применять в лабораторных условиях при наличие любого фиксатора частоты, например, панорамный измеритель Р2–61. Так как диаметр образца можно измерить с достаточной точностью, то предложенный метод удобен для оценки диэлектрической проницаемости тонких образцов.