Колебания напряжения в узлах нагрузок систем электроснабжения (СЭС) возникают при наличии электроприёмников, имеющих повторно-кратковременные режимы работы с быстрым изменением режима и потребляемой мощности. К таким электроприемникам относятся [4]: дуговые сталеплавильные печи (ДСП), прокатные станы, установки дуговой и контактной электросварки, нагнетательные насосы и др.
Колебания напряжения отрицательно влияют на вращающиеся электрические машины, возможен выход из строя БСК. Кроме того, одним из главных негативных последствий колебания напряжения является эффект фликера, т.е. субъективного ощущения неустойчивости восприятия зрительным органом по причине изменения во времени спектрального состава или яркости источника света [1]. Нарушение показателя качества электроэнергии (колебание напряжения) вызывает нарушение условий труда и жизни человека. Актуальность разработки цифровых динамических моделей для оценки дозы фликера представлена в [2], где автор обращает внимание на необходимость рассматривать «графики колебаний напряжения без искусственного их разделения на отдельные участки по тому или иному принципу».
Колебания напряжения возникают в сетях различных классов напряжения. В работе [7] на конкретных примерах сетей низкого и среднего напряжения Испании авторы приводят методики анализа колебаний напряжения в соответствии с международным стандартом IEC 61000–2–12.
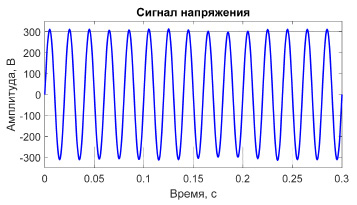
Рис. 1. Колебания напряжения
На рис. 1 представлена осциллограмма напряжения, где размах колебания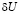 
может быть определён из разности максимального 
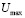и минимального 
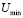значениями огибающей напряжения:
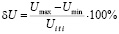, (1)
Колебания напряжения в системах электроснабжения следует рассматривать как модулированное колебание синусоидальной величины при изменении амплитуды сигнала. В этом случае простейшее амплитудно-модулированное колебание может быть записано по формуле
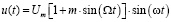, (2)
где Um – амплитудное значение напряжения, В; m – глубина модуляции, В; w – угловая частота питающей сети, рад/с; W – угловая частота огибающей, рад/с.
В то же время колебания напряжения можно представить в виде суммы синусоиды с частотой питающей сети а=50 Гц и двух дополнительных синусоид с частотами близкими, но не равными промышленной частоте [9]:
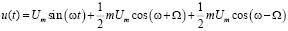, (3)
где ω±W называют боковыми частотами.
Детальный анализ причин и последствий возникновения колебаний напряжения в системах ограниченной мощности (при питании от автономных источников энергии) представлен в работе [9].
Теория и моделирование
Каждый электроприёмник, являющийся причиной возникновения колебаний напряжения имеет свой специфический график электрических нагрузок, определяемый технологическими условиями производства. Для решения задач моделирования, расчета и анализа режимов работы систем электроснабжения при условии возникновения колебания напряжения в узлах нагрузок следует учитывать особенности каждого типа электроприёмников. В работе [6] авторами исследуется проблема колебания напряжения в узлах с асинхронными двигателями, работающими с резкопеременной нагрузкой. При этом освещается применение теории вероятности в качестве математического аппарата, поскольку величины потребляемой двигателем активной P(t) и реактивной Q(t) мощностей могут быть учтены как случайные величины. В таком случае характеристиками режима работы узла нагрузок выступают функции математического ожидания M[P(t)], M[Q(t)] и дисперсии D[P(t)] и D[Q(t)]. На базе представленного анализа автор приходит к выводу, что для расчета колебания напряжения, вызванной работой асинхронных двигателей с резкопеременной нагрузкой целесообразно «использовать решетчатые модели графиков электрических нагрузок и напряжения сети, интерполированные сплайн-функциями первой степени» [6].
В работе [5] автор анализирует связь колебаний напряжения на шинах питания одиночных и параллельных ДСП с функциями токов, которые зависят от регуляторов мощности ДСП и характера технологического процесса. Представленная в [5] методика позволяет анализировать режимы работы систем электроснабжения с ДСП по условиям электромагнитной совместимости.
Одним из существующих подходов анализа колебаний напряжения является применение преобразования Стоквелла (S-transform), которое является некоторой модификацией оконного преобразования Фурье (ПФ). Отличие в данном случае заключается в дополнительном масштабировании оконной функции по частоте [7].
В последнее время для решения широкого круга задач цифровой обработки сигналов находит вейвлет преобразование [3].
Вейвлет преобразование (ВП) функции напряжения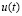 
при изменении параметров масштаба и сдвига по времени может быть реализовано путём свёртки 
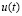и вейвлет функции 
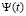[10]:
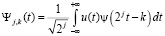, (4)
где k и j сдвиг по времени, и масштабирующий коэффициент, соответственно, а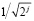 
нормирующий показатель. Преимущество ВП заключается в отсутствии эффекта «растекания спектра», а также в возможности трёхмерной интерпретации выходных данных (амплитуда-частота-время).
Для цифровой обработки сигналов параметров режима системы электроснабжения удобнее пользоваться дискретным вейвлет преобразованием (ДВП), что позволит выявить частоту огибающей при колебаниях напряжения. Аппарат ДВП на примере простейшего вейвлета Хаара ранее был представлен в [3], где также приводится схема частотной декомпозиции исследуемого сигнала.
Предлагаемый алгоритм. Численный эксперимент
Алгоритм для идентификации колебаний напряжения может быть представлен в следующем виде:
1. Исходный сигнал напряжения u(t) возводится в квадрат. При этом получаем сигнал, где представлены различные частотные составляющие:
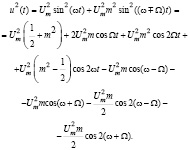(5)
2. Производится ДВП сигнала u2(t) с такой глубиной разложения [3], чтобы разделить по частотным составляющим в соответствии с алгоритмом Малла.
3. По детализирующим коэффициентам уровня разложения d1 и d2 определяются интервалы времени, на которых происходит изменение режима – возникновение колебаний напряжения.
3. Определяется энергия спектра вейвлет коэффициентов по каждому частотному диапазону. Если энергия спектра окажется менее заданного порогового уровня погрешности Δε, то данные коэффициенты могут быть отброшены, т.к. это означает отсутствие частотных составляющих в данном диапазоне.
4. По вейвлет коэффициентам, имеющих значение энергии спектра выше Δε производится обратное ДВП (восстановление) сигнала.
5. На основе быстрого ПФ определяются частоты и амплитуды дополнительных частот, определяющих характер колебания напряжения. При этом ПФ производится только в отрезке времени, полученном в п. 3 настоящего алгоритма.
Проиллюстрируем предложенный алгоритм численным экспериментом. Пусть сигнал напряжения (рис. 1) задан функцией
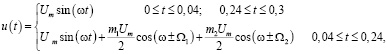(6)
где на интервале времени от 0,04 (с) до 0,24 (с) (короткие промежутки времени выбраны для наглядности представляемого алгоритма) будет присутствовать колебание напряжения с двумя группами боковых частот (ω±Ω1)= (50±3) и (ω±Ω1)= (50±8). Глубина модуляции принята равной для обеих частот и составляет
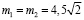(В).
В соответствии с предлагаемым алгоритмом после возведения в квадрат функции напряжения, описанной формулой (6), производится ДВП полученного сигнала. Анализ интервалов времени, на которых происходит изменение режима производится с помощью детализирующих вейвлет коэффициентов (рис. 2).
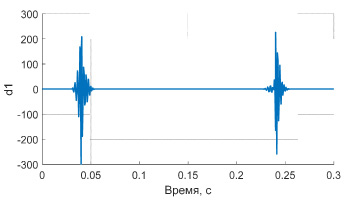
Рис. 2. График детализирующего вейвлет коэффициента d1
Характерный всплеск амплитуды высокочастотного вейвлет коэффициента d1 дает информацию о начале отрезка появления колебания напряжения в сети
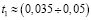
и завершения данного отрезка
,
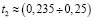что с достаточной степенью точности соответствует заданной функции (6).
Далее определяются вейвлет коэффициенты, чья энергия спектра превышает заданный пороговый уровень (в относительных величинах к основной частоте). В нашем случае такими коэффициентами определены d7 и d9 (рис. 3, 4).
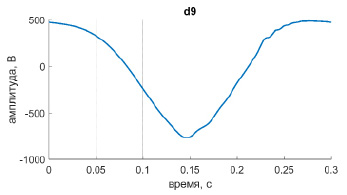
Рис. 3. Вейвлет коэффициент d9
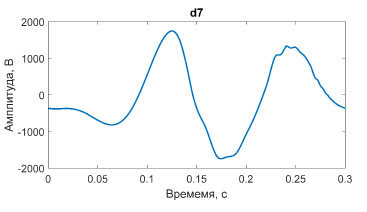
Рис. 4. Вейвлет коэффициент d7
По матрицам значений выделенных (имеющих существенный вклад в энергию спектра) вейвлет коэффициентов производится обратное вейвлет преобразование, другими словами – восстановление сигнала определённого частотного диапазона. На завершающем этапе производится быстрое преобразование Фурье (БПФ) восстановленных по вейвлет коэффициентам (рис. 3, 4) частотных компонент. Итогом БПФ становится определение амплитуды и частоты, присутствующих в сигнале боковых частот, которые характеризуют размах колебаний напряжения.
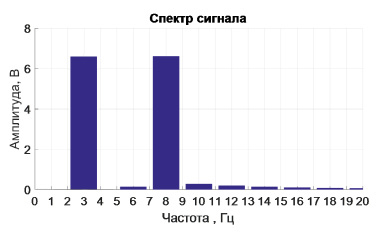
Рис. 5. Спектр частот, характеризующих колебания напряжения
Полученные данные соответствуют амплитудам, частотам и интервалами присутствия исходному сигналу напряжения, заданного по условию (6), что позволяет судить о корректной работе предложенного алгоритма. Данный подход может быть использован при цифровой обработке сигналов, характеризующих параметры режимов систем электроснабжения, что позволит в дальнейшем повысить точность анализа режимов, при которых происходят колебания напряжения.
Выводы
Вейвлет преобразование является удобным математическим аппаратом для анализа нестационарных режимов работы СЭС, позволяющим определять не только частотные компоненты исследуемых сигналов (напряжения, тока и др.), но и локализовать данные функции по времени. Данное обстоятельство позволяет рекомендовать применение вейвлет преобразования для анализа колебаний напряжения в узлах нагрузок СЭС. В представленном алгоритме показана возможность определения интервалов времени, на которых возникают колебания напряжения. Кроме того определены (найдены частоты и амплитуды) дополнительные частотные составляющие, характеризующие размах и длительность колебаний напряжения. Предложенный метод позволяет в отличие от ПФ лишён недостатка эффекта «растекания спектра» и отсутствует необходимость выбора типа и ширины окна, как это требуется для оконного ПФ.