При обработке деталей поверхностным пластическим деформированием (ППД) в поверхностном слое детали происходят необратимые пластические деформации, результатом которых является упрочнение поверхностного слоя, а также формирование остаточных напряжений. Эти показатели качества поверхностного слоя преимущественно определяются на основе проведения экспериментальных исследований. В связи с этим актуальным является определение математических моделей расчета глубины упрочненного слоя и закона распределения остаточных напряжений по глубине упрочненного слоя.
Одной из первых зависимостей для расчета глубины упрочнения является формула, полученная Хейфецом С.Г. [1] на основе контактной задачи с допущением, что сила деформирования приложена в точке при этом не учитываются особенности распределения контактных напряжений по площади контакта между деформирующим роликом и обрабатываемой поверхностью. Эта формула имеет вид
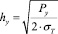 (1)
(1)
где Pу - сосредоточенная сила деформирования, приложенная в центре площади контакта; σT - предел текучести обрабатываемого материала.
В результате последующей экспериментальной проверки было обнаружено, что приведенная зависимость с достаточной степенью точности подтверждается при обработке деталей с относительно малыми радиусами (5…15 мм) и при значительных силах, действующих на ролик. Для валов большего диаметра при обкатывании с большими силами результаты получаются завышенными на 30%...50%.
Чтобы устранить расхождения между теоретическими и экспериментальными данными И.В. Кудрявцевым и Г.Е Петушковым [1] была предложена модификация формулы (1) принимающая вид
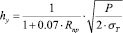 (2)
(2)
где приведенный радиус определяется по формуле
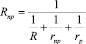 (3)
(3)
где R – радиус детали; rпр – профильный радиус тороидального ролика; rp – радиус ролика.
Эта формула применяется, когда в качестве деформирующих роликов используются шарики и профильные (тороидальные) ролики. Для других типов роликов, например, конических, наиболее часто применяемых в производственной практике эта задача не решена.
Поскольку при обработке ППД ролики контактируют с обрабатываемой деталью по определенной площади, то необходимо искать решение от распределения напряжений по поверхности контакта.
Для определения распределения напряжений в теле детали от сосредоточенной силы, приложенной к поверхности полубесконечного тела, в теории упругости приводится следующая система уравнений [3] (см. рис. 1):
Систему уравнений (4)…(7) примем в качестве основы для дальнейшего анализа и получения расчетных формул определения напряжений в теле детали в зависимости от контактных напряжений.
Рассмотрим уравнение (4). Предположим, что на некоторой глубине hy напряжение hу достигает предела текучести σТ, а рассматриваемая точка в теле детали расположена на линии действия сосредоточенной силы Р. Это соответствует условию r=0. Выполнив необходимые преобразования, получим
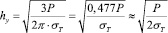 (8)
(8)
Это фактически соответствует формуле (1).
Полученный результат указывает на источники расхождения расчетных значений, выполненных по формуле (1) с экспериментальными данными.
Из системы уравнений (3)…(7), видно, что действие силы Ру на напряжение в детали убывает от точки ее приложения обратно-пропорционально третьей степени расстояния между ними. Следовательно, чем больше площадь контакта при одной и той же силе деформирования, тем больше будут расхождения с экспериментальными данными, полученными по формуле (1).
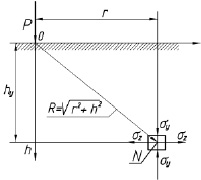
Рис.1. Схема образования напряжений в поверхностном слое на глубине hу и расстоянии r от сосредоточенной силы Р, приложенной в точке к границе полубесконечного тела
Для оценки влияния распределенных контактных напряжений по площади контакта на глубину упрочнения, и возможности сравнения этих результатов с методиками других авторов определения напряжений в поверхностном слое, будем пользоваться только уравнением (5), так как остальные составляющие, как показали предварительные расчеты, влияют значительно слабее на напряжения в детали, поэтому ими в первом приближении можно пренебречь.
Для выяснения основных закономерностей влияния контактных напряжений на напряжения в поверхностном слое смоделируем площадь контакта в виде круга и изменяющимся в пределах этого круга распределением напряжений по разным законам.
Введем в рассмотренные полярные координаты ρ, θ с началом системы координат в центре круга. Выделим в круге сектор с углом раствора dθ. Элементарная площадка контакта расположенная в этом секторе на расстоянии s от начала координат равна sdθds, а элементарная сила, приложенная к этой площадке можно вычислить по зависимости рsθ = σsθ sdθds. Будем предполагать, что напряжение σsθ в пределах контакта зависит только от расстояния между началом координат и рассматриваемой точкой и не зависит от угла θ.
Применяя решение (5), найдем суммарное действие от напряжений, распределенных в круге, расположенного к полубесконечному телу на напряжения в точке этого тела, расположенной на оси координат у, приложенной к центру круга перпендикулярно поверхности
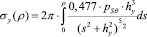 (10)
(10)
где ρ – переменный радиус круга.
Рассмотрим два различных закона распределения напряжений в круговом контакте: 1)напряжения, изменяющиеся по закону Герца [2] и 2) постоянном напряжении по всей площади контакта в круге (рис.2,а), значение которого равно максимальному напряжению в первом случае.
При обработке ППД шариками плоской поверхности размеры контактной зоны не превышают шести миллиметров.
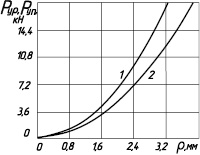
Как видно из графика (рис.2,б) разница в усилиях деформирования начинает существенно сказываться при диаметрах кругового контакта больше двух миллиметров. Исходя из этого, можно предположить, что существенное влияние на напряженное состояние в теле детали при одной и той же площади контакта будет оказывать максимальные напряжения в центре контакта, а не закон распределения напряжений.

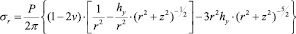 (4)
(4)
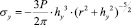 (5)
(5)
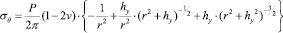 (6)
(6)
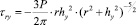 (7)
(7)
где r и hy - координаты точки в теле детали, в которой рассматривается напряженное состояние от сосредоточенной силы Р; –коэффициент Пуассона (рис.1).
а) б)
Рис.2. Зависимости изменения напряжений по ширине контакта при разных законах распределения напряжений:-по убывающему закону от центра площадки σр и при постоянном напряжении σп на всей площади контакта равном максимальному значению в предыдущем случае (а); изменение усилия деформирования от диаметра кругового контакта (б). 1 – для постоянного напряжения, 2- для напряжения, изменяющегося по закону Гука
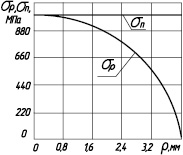
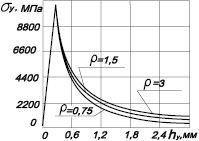
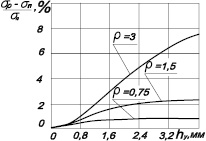
Изменение напряжений по глубине поверхностного слоя от распределенных напряжений в круговом контакте, представленные на рис.3. подтверждают многочисленные экспериментальные данные. Напряжения в поверхностном слое сначала растут от нуля до некоторого максимального значения, а затем уменьшаются.
а) б)
Рис.3. Изменение напряжений по глубине поверхностного слоя при разных значениях радиуса кругового контакта (а); б)- процентное отношение изменения напряжений по глубине поверхностного слоя при постоянном и изменяющемся по закону Герца напряжениях в круговой контактной зоне
Проведем горизонтальную прямую на расстоянии от начала координат, которая соответствует пределу текучести σТ. Точки ее пересечения с кривой распределения напряжений в теле детали определяют координаты перехода напряжений из упругой области в область пластически деформированного металла. Точка пресечения, которая расположена на убывающей ветви кривой напряжений, определяет координату глубины упрочненного слоя. Как следует из графика рис.3в большему значению радиуса контакта, соответствует большая глубина упрочнения, так как при этом увеличивается и усилие деформирования. Различие между глубиной упрочнения при распределении напряжений по убывающему закону и при постоянной силе деформирования не превышает 10% (рис.3.б), причем это различие увеличивается пропорционально площади контакта, как установлено многочисленными экспериментальными данными..
На рис.4 показаны графики изменения глубины упрочнения, рассчитанные по формуле (1) и формуле (10). Как видно из этих графиков, чем больше размеры контактной зоны, тем больше расхождение между глубинами упрочнения, как и проявляется в эксперименте.
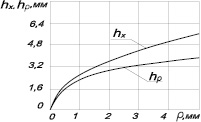
Рис. 4. Сравнительные графики глубины упрочнения по формуле Хейфеца ( hх ) и формуле (10) (hρ )

