Одной из основных частей многороликовых ротационных инструментов для обработки поверхностей деталей ППД является опорный конус, выполняемый в виде прямого кругового конуса. Назначением этой детали инструмента является установка роликов на требуемый задний угол и возможность настройки роликов на заданную глубину их внедрения в обрабатываемую поверхность.
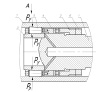
Рис. 1. Установка роликов в раскатнике с опорным конусом. 1-шомпол; 2 – рычаг: 3- конус опорный; 4- сепаратор; 5- ролик; 6- гайка. 7 – обрабатываемая заготовка
В ряде случаев, при необходимости обеспечения самозатягивания или уменьшения осевой силы, действующей на инструмент, ролики устанавливают на угол по отношению к оси детали для перемещения по винтовой линии соответствующей подаче и вычисляемой по формуле:
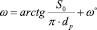 (1)
(1)
где ` - дополнительный угол компенсирующий проскальзывание (` = 10` … 15`)
So – подача инструмента, мм/мин; dp - диаметр ролика, мм.
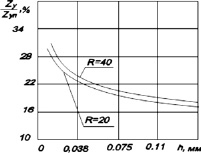
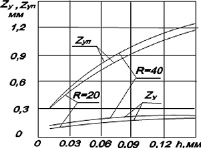
Если = 0, то контакт между роликами и опорным конусом при отсутствии нагрузки будет линейным, так как оба тела соприкасаются по образующим. Поворот роликов на угол самозатягивания превращает линейный контакт в точечный. В случае приложения нагрузки этот контакт превращается в эллиптический с площадью небольших размеров. На рис. 2 изображено соотношение между площадями пластического отпечатка, вычисленными по формуле (3) [3] и упругого контакта вычисленными по формулам Герца [1].
а б
Рис.2. Зависимость ширины контактной зоны от глубины внедрения деформирующего ролика в обрабатываемую деталь при упругопластическом и упругом контактах (a) и их процентное отношение (б): zуп – упругопластический контакт; zy – упругий контакт
Как видно из рис. 2,а площадь контакта пластически деформируемой зоны между обрабатываемой поверхностью с роликами значительно больше, чем площадь контакта между роликами и опорным конусом. При равенстве сдавливающих сил напряжения пропорциональны площадям контактов, поэтому максимальное напряжение будет приложено на упругом контакте, что и определит в основном усталостную прочность роликов и опорного конуса. Условия нагрузки на обрабатываемую поверхность определяют необходимые параметры качества обработанной поверхности и являются заданными. В связи с этим необходимо изменить условия деформирования между роликами и опорным конусом, таким образом, чтобы уменьшить между ними контактные напряжения. Для этого, очевидно, что при установке на угол самозатягивания, ролики и опорный конус должны соприкасаться по своим образующим на всей длине контакта. Этого можно достичь изменением формы боковой поверхности роликов или опорного конуса. С точки зрения технологичности предпочтительным является изменение формы опорного конуса, так как роликов значительно больше и очень часто используются готовые ролики с прямолинейной образующей из конических подшипников.
Решим эту задачу отдельно для обработки вала и отверстия. С этой целью рассмотрим взаимодействие конических деформирующих роликов и опорного конуса.
При параллельном положении образующих ролика и опорного конуса в соответствии с теорией Герца [1], их сближение определяется зависимостью:
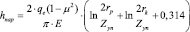 (2)
(2)
где Zуп - ширина упругого контакта между роликом и опорным конусом вычисляется по формуле
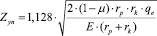 (3)
(3)
В приведенных формулах величины радиусов ролика rp и опорного конуса rk приняты равными среднему значению.
При взаимно перпендикулярном положении осей ролика и опорного конуса их сближение определяется зависмостью:
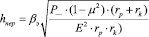 (4)
(4)
При повороте ролика на угол самозатягивания сближение будет иметь промежуточное значение между величинами вычисленными по предыдущим двум формулам.
Так как в литературе нет формул для вычисления сближения при произвольном угле пересечения двух цилиндрических тел, что предположим, что в зависимости от угла самозатягивания сближение будет иметься по закону:
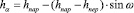 (5)
(5)
Откуда следует, что при = 00 и = 900 сближение будет совпадать с граничными условиями задачи (2) и (4).
Глубина внедрения роликов в поверхность опорного конуса при их взаимном нагружение является переменной по длине контакта, причем в контакте находится только часть длины ролика. Радиус вектор ОМ проведенный из произвольной точки М образующий перпендикулярно оси опорного конуса определит уравнение поверхности вращения соприкасающейся с деформирующим роликом по прямой линии (рис.1)
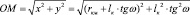 (6)
(6)
где x и y – текущие координаты уравнения искомой поверхности вращения. Поверхность прямого кругового конуса для тех же размеров обрабатываемой поверхности изменяется по закону:
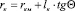 (7)
(7)
Длина упругого контакта равна значению lk при условии h1=0. На рис. 1 представлены зависимости изменения сближения роликов с опорным конусом по длине контакта рассчитанные по формулам (2,4,5).
Учитывая, что при упругом взаимодействии напряжения пропорциональны деформациям, можно считать, что эпюра контактных напряжений будет пропорциональна эпюре сближения роликов с опорным конусом. Следовательно, при установке роликов на угол самозатягивания, напряжения распределены по длине контакта неравномерно. Из формулы (5) видно, что равномерное распределение деформаций и напряжений, имеет место, когда зависимость (2) равна по численному значению зависимости (4). Таким образом форма поверхности опорного конуса описываемого уравнением (6) будет оптимальной с точки зрения минимизации напряжений на упругом контакте. Из этого уравнения следует что при = 00, оно превращается в уравнение прямого кругового конуса:
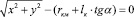 (8)
(8)
Полагая затем =00, найдем:
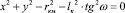 (9)
(9)
и, принимая соотношение постоянных величин в виде
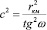 (10)
(10)
получим уравнение гиперболоида вращения:
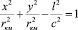 (11)
(11)
Это линейчатые поверхности, следовательно, и поверхность описываемая уравнением (11), при произвольных и , тоже будет линейчатой.
В последнее время режим самозатягивания находит широкое применение для обработки длинномерных деталей, особенно при совмещенной обкатке резанием и ППД роликами гладких валов и отверстий. В последнем случае необходимо создать максимально возможную силу сцепления деформирующих роликов с обрабатываемой поверхностью. Как показывают исследования работы обкатников работающих в режиме самозатягивания, усилие обкатывания которых обеспечивает момент преодолевающий силы резания, иногда возникает проскальзывание роликов, причем проскальзывание роликов по поверхности опорного конуса наступает при меньшем усилии по сравнению с проскальзыванием роликов относительно обрабатываемой поверхности. Предположительно, это происходит по причине неплотного прилегания деформирующих роликов, а только по их концам, так как за счет установки роликов на угол самозатягивания между внутренней поверхностью опорного конуса и средней частью роликов образуется зазор (рис. 1).
Определим оптимальную форму внутренней поверхности опорного конуса для обработки валов при условии соприкосновения роликов по прямой линии с опорным конусом для чего будем предполагать, что деформирующие ролики опираются не на коническую, а на цилиндрическую поверхность отверстия конуса, это допустимо в виде малого угла конусности опорного конуса (не более 20).
В этом случае радиус цилиндрической поверхности примем равным:
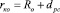 (12)
(12)
В этом предположении, при совместном сечении ролика и конуса плоскостью А – А (рис. 1) в сечении образуется пересекающиеся эллипс и отрезок прямой, концы которого расположены на эллипсе в точках А и Б. Уравнение эллипса образующегося в сечении будет иметь вид:
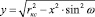 (13)
(13)
Подставляя в это уравнение координаты точек С и Б, то есть Х и вычитая правую часть из радиуса, то получим величину максимального зазора.
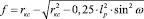 (14)
(14)
С точки зрения технологичности изготовления предпочтительней изменить форму опорного конуса, чем деформирующих роликов. В зависимости от применяемой технологии, целесообразно также заменить эллипс окружностью. Радиус этой окружности можно вычислить по формуле:
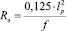 (15)
(15)
Полученные формулы позволяют обеспечить обработку рабочей поверхности опорного конуса с заданной формой и получить контакт соприкосновения деформирующего элемента с ним по линии.

