Развитие сверхкритических технологий требует знания особенностей теплопереноса вблизи критической точки и создания на этой основе новых подходов к системам управления процессами в различных СКФ устройствах. В частности, применение СКФ в ракетно-космической технике требует изучения особенностей теплопереноса в СКФ при воздействии сильных перегрузок, а также при различных условиях тяготения в перспективных разработках применения СКФ-технологий при освоении Луны и планет солнечной системы.
Численные и экспериментальные исследования теплопереноса в замкнутом объеме, наполненном сверхкритическим флюидом, особенно интенсивно развивались в последние два десятилетия, в частности благодаря международным экспериментам, проведенным на борту орбитальных станций МИР и МКС. Было обнаружено, что при нагреве или охлаждении границ объема с СКФ наблюдается существенное ускорение прогрева/охлаждения среды, когда начальная температура в объеме приближается к критической температуре [2–8]. При этом температура, давление и плотность существенно меняются вблизи стенки и практически постоянны в «толще» (англ. bulk) среды. Поскольку слой жидкости в непосредственной близости от стенки расширяется, а среда в толще сжимается, то внешне процесс нагрева выглядит как сжатие основной толщи жидкости поршнем. Поэтому такая особенность процесса нагрева получила название «пистон-эффекта» (англ. piston-effect).
Важной характеристикой является характерное время прогрева толщи жидкости (характерное время пистон-эффекта), tпе. В работе [9] получено аналитическое решение уравнения передачи тепла от мгновенно нагретой стенки к жидкости в отсутствие силы тяжести (g=0). При выводе уравнения предполагалось, что температура стенки постоянна, перенос тепла в пристеночный слой происходит за счет теплопроводности, а толщина пристеночного слоя много меньше размера всей области нагрева. При этом пристеночный слой расширяется изобарически, а толща жидкости сжимается адиабатически. из решения следует, что время пистон-эффекта определяется формулой:
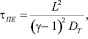 (*)
(*)
где L – характерный размер области; γ = сP/сV; сP – теплоемкость при постоянном давлении, сV – теплоемкость при постоянном объеме, DT=λ/ρсP, λ – коэффициент теплопроводности, ρ – плотность.
При достижении времени пистон-эффекта температура в толще жидкости достигает величины 0,572 от температуры нагретой стенки.
Зная характер зависимости входящих в формулу величин от параметра e, можно оценить, как характерное время нагрева меняется при приближении к критической точке. В работе [10] использовались зависимости DT ~ ε 0,66 и γ ~ ε -1,13, что дает τПЕ ~ ε 1,6 .
Целью данной работы является исследование влияния различных значений силы гравитации на ускоренный прогрев замкнутого объема СКФ. Расчеты проводились для одномерного случая с использованием уравнений Навье-Стокса и уравнения состояния Ван-дер-Ваальса.
Математическая модель
Безразмерная система уравнений состояния, баланса энергии, движения и неразрывности имеет вид:
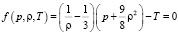 , (1)
, (1)
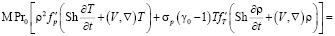
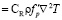 , (2)
, (2)
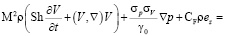
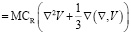 , (3)
, (3)
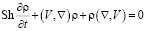 . (4)
. (4)
Здесь введены следующие безразмерные комплексы (курсивом обозначены размерные величины):
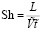 – число Струхала, L – масштаб длины,
– число Струхала, L – масштаб длины, 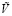 – масштаб скорости и
– масштаб скорости и 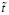 – масштаб времени;
– масштаб времени; 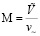 – число Маха,
– число Маха, 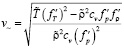 – скорость звука при масштабных термодинамических параметрах
– скорость звука при масштабных термодинамических параметрах 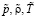 , где
, где 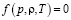 ;
;
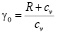 – показатель адиабаты или адиабатическая постоянная;
– показатель адиабаты или адиабатическая постоянная;
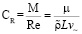 ,
, 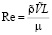 – число Рейнольдса. Параметр CR позволяет сопоставить влияние трения при скоростях диффузионных процессов с влиянием трения, возникающего при движении со звуковыми скоростями в среде с масштабной плотностью в масштабном объеме.
– число Рейнольдса. Параметр CR позволяет сопоставить влияние трения при скоростях диффузионных процессов с влиянием трения, возникающего при движении со звуковыми скоростями в среде с масштабной плотностью в масштабном объеме.
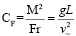 ,
, 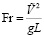 – число Фруда. Параметр CF соотносит потенциальную энергию пробной массы при заданном тяготении на уровне масштабной высоты с кинетической энергией, которую приобретает эта масса, двигаясь со скоростью звука.
– число Фруда. Параметр CF соотносит потенциальную энергию пробной массы при заданном тяготении на уровне масштабной высоты с кинетической энергией, которую приобретает эта масса, двигаясь со скоростью звука.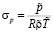 – коэффициент, характеризующий уклонение выбранного масштаба давления от давления совершенного газа при выбранных масштабах плотности и температуры.
– коэффициент, характеризующий уклонение выбранного масштаба давления от давления совершенного газа при выбранных масштабах плотности и температуры.
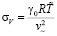 – коэффициент, характеризующий уклонение квадрата скорости звука в совершенном газе при выбранном масштабе температуры от квадрата скорости звука исследуемого газа при масштабных термодинамических параметрах.
– коэффициент, характеризующий уклонение квадрата скорости звука в совершенном газе при выбранном масштабе температуры от квадрата скорости звука исследуемого газа при масштабных термодинамических параметрах.
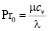 – число Прандтля. Формально
– число Прандтля. Формально 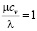 однако на практике параметр
однако на практике параметр 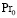 указывает отклонение этого отношения от единицы.
указывает отклонение этого отношения от единицы.
Представленная модель использовалась ранее в работе [1] для расчетов распада разрывов температуры и давления в ячейке СКФ при γ=0.
Расчеты проводились для вертикальной одномерной области высотой L = 1 см в поле силы тяжести, направленной вниз. Рабочее тело – шестифтористая сера (SF6). В начальный момент времени распределение давления и плотности соответствуют заданной величине ускорения свободного падения, температура постоянна по высоте и соответствует заданной сверхкритической температуре Тнач. Температура верхней границы мгновенно возрастает на величину 1 мК и поддерживается постоянной во время расчета. Нижняя граница считается адиабатической.
Для вычисления безразмерных комплексов, входящих в уравнения (1)–(4) использовались следующие константы (для SF6): cv = 1000 дж/кг·град, λ = 1,2 вт/м·град, μ = 40·10–6 Па•с, R = 56,9 дж/кг·град., γ0 = 1.0569 и масштабы переменных: L = 10–2 м, 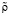 =rкр = 744 кг/м3,
=rкр = 744 кг/м3, 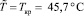 ,
, 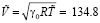 м/c,
м/c, 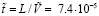 c.
c.
В расчетах определялись зависимости от времени распределений температуры, давления, плотности и скорости по высоте при различных начальных значениях температуры и ускорения свободного падения.
Методика и результаты расчетов
Для расчетов была применена вычислительная схема, основанная на явном методе конечных разностей. Шаг по пространству h=10–3, шаг по времени h(h)0.5.
Для определения начального равновесного распределения давления и плотности, соответствующего заданному значению ускорения свободного падения, применялись два способа: расчет с помощью численной реализации описанной выше математической модели и расчет по формуле
 . (**)
. (**)
Формула получена путем интегрирования уравнения движения (3) при условии равенства скоростей нулю, постоянства температуры вдоль вертикальной оси и выполнении уравнения состояния Ван-дер-Ваальса (1).
Предварительные расчеты показали, что распределения, полученные этими двумя способами, практически совпадают. С целью экономии машинного времени в дальнейших расчетах использовались начальные распределения плотности и давления, полученные с помощью формулы (**).
Расчеты были проведены для g=0, g=g0=9.81 м/с2 и для перегрузки g=5g0 и g= 10g0.
На рис. 1 представлены распределения плотности для этих значений ускорения свободного падения при двух значениях разности начальной и критической температуры, ΔТ = Тнач–Ткр = 10 мК и 500 мК. При ΔТ = 10 мК наблюдается характерный перегиб при z=0,5 и ρ=1, в то время как даже на небольшом удалении от критической точки (ΔТ=500 мК) профили плотности практически линейны для всех значений g.
На рис. 2 приведены зависимости приращения безразмерной температуры δТ = Т–Тнач в центре расчетной области (z = 0,5) от времени для различных значений ускорения свободного падения. Разница между начальной и критической температурой составляет ΔТ = 10 мК, количество узлов расчетной сетки n=1003. При отработке методики расчетов были проведены вычисления для различного количества узлов: n=403, 1003 и 10003. Результаты этих расчетов для g=0 приведены на вставке рис. 2. Оказалось, что кривые для 1003 и 10003 узлов практически совпадают, поэтому в дальнейшем все расчеты проводились для 1003 узлов.
Величина характерного времени пистон-эффекта τПЕ определялась по зависимостям температуры в центре расчетной области от времени. Следуя работе [8] предполагалось, что τПЕ соответствует времени, за которое температура в толще среды достигла величины 0,572 от разницы между начальной и конечной температурой. В нашем случае эта разница составляет Ткон.–Тнач = 1 мК, а безразмерная величина приращения температуры в толще, соответствующая величине 0,572(Ткон.–Тнач.), составляет δТПЕ = 1,7910–6. Тогда, например для ΔТ = 10 мК и g = g0 (см. рис. 2), τПЕ = 0,25 с
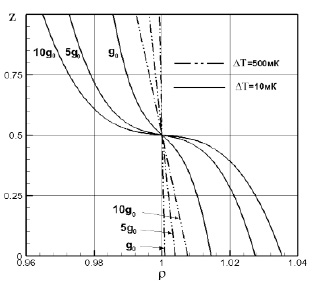
Рис. 1. Распределения плотности для различных значений ускорения свободного падения при ΔТ = Тнач–Ткр = 10 мК и 500 мК
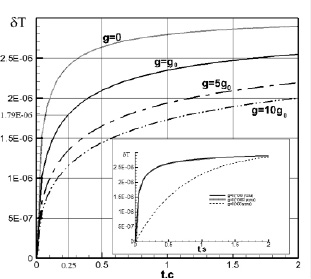
Рис. 2. Зависимости приращения безразмерной температуры δТ = Т–Тнач в центре расчетной области (z = 0,5) от времени для различных значений ускорения свободного падения
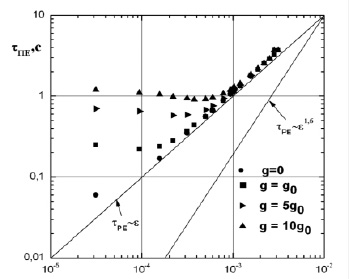
Рис. 3. Зависимости τПЕ от величины e для различных значений g
Разность между начальной и критической температурой ΔТ = Тнач–Ткр менялась от 10 мК до 1000 мК, что соответствует изменению e в пределах 3·10–5 < e < 3·10–3 . На рис. 3 представлен график зависимости τПЕ от величины e для различных значений g. из графика видно, что при ε > 10–3 зависимости τПЕ от e для всех значений ускорения свободного падения и для невесомости (g=0) практически совпадают. При этом величина наклона графика близка к единице, т.е. τПЕ ~ e.
Такой наклон соответствует представленной выше формуле (*), поскольку при сV = const, λ = const (что принято в нашей модели) и при
g >> 1 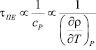 ,
,
а в соответствии с принятым в модели уравнением Ван-дер-Ваальса 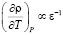 , т.е.
, т.е. 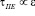 .
.
При ε < 10–3 наклон графика для g=0 практически не меняется, в то время как при наличии гравитации время пистон-эффекта значительно увеличивается. для наибольшей величины ускорения свободного падения это отличие максимально. Например, для ε ≈10–4 время пистон-эффекта при g= 10g0 на порядок меньше чем при невесомости. При приближении к критической точке, чем больше g, тем раньше характерное время пистон-эффекта начинает отличаться от его значения в невесомости.
Заключение
На основе уравнений Навье-Стокса и уравнения состояния газа Ван-дер-Ваальса проведено численное исследование особенностей процесса ускоренного прогрева сверхкритической шестифтористой серы для одномерного случая в диапазоне 3·10–5 < e < 3·10–3 при различных условиях гравитации. Получено, что при приближении к критической точке начиная со значения ε ≈10–3 характерное время ускоренного прогрева (время пистон-эффекта τПЕ) существенно увеличивается по сравнению с условиями невесомости. Причем, чем больше ускорение свободного падения, тем раньше при приближении к критической точке эта разница начинает проявляться и тем больше она по величине.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант № 15–01–02012).

