Методы комбинаторного моделирования модульных структур кристаллов используются для получения новых модульных структур с вероятными топологиями модулей, производными от модуля «материнской» структуры, идентификации генетической взаимосвязи этих модульных структур с исходной структурой, разработки общих алгоритмов и кодов структурного формирования [1, 2, 13 – 20]. для достижения этих целей необходимо последовательно решить совокупность комбинаторных задач, в том числе и задачу выбора структурного модуля – одну из значимых комбинаторных задач. Решение данной задачи осуществляется разбиением кристаллического 3D пространства на ячейки произвольной формы – поликубы (полимино) с последующим их заполнением модулями (молекулами или атомным ансамблем), удовлетворяющими определенным условиям [13 – 16].
С другой стороны структурные модули, которые могут быть использованы для модульного дизайна, можно получить в результате разбиения кристаллического пространства на одинаковые подпространства–ячейки. В этих ячейках окажутся идентичные структурные единицы – модули, связанные между собой достаточно простыми и вполне определенными элементами симметрии (плоскости отражения, поворотные оси, центр инверсии) [7 – 9, 12, 22].
Модулярные и инверсионно модулированные модулярные структуры
Проведем сравнительный анализ генетического кода некоторой модулярной структуры в соответствии с символикой, веденной в [2 – 6, 10, 11]:
R33{M(G30)(||i||,m,||k||)}[S(LC)i (G33(z))]
со структурным кодом той же модулярной структуры
R33{M(G30)(||CP||)}[(LC)33 (G33(z))].
Используемые выше обозначения [11]:
M (G30) – состав модуля с локальной симметрией G30,
||CP|| – матрица кодов упаковки модулей, заданная одним из возможных способов,
LC – решеточный комплекс, в соответствии с образом которого упаковка данных модулей обладает симметрией G33,
||i|| – матрица индексов ветвления центрального модуля М (первичного ядра модулярной структуры), которая определяется количеством его вершин (iv), ребер (ir) и граней (ig), т.е. ||i|| = (iv, ir, ig), и характеризует вид инверсионности,
m [0,1,2,…] – целочисленный индекс, характеризующий размерный параметр локальной структуры (модулированность модулярной структуры),
||k|| – матрица индексов ветвления вторичных ядер, изоморфная матрице индексов ветвления ||i||.
Идентичность структуры символьных записей кодов позволяет свести анализ к сравнению информационной значимости двух групп символов (||i||,m,||k||) и (||CP||).
Для фиксированного варианта разбиения 3D пространства использование матриц индексов ветвления и индексов роста при значениях m = 0 и 1 приводит к заполнению соседних пространственных ячеек и образованию плотных локальных структур, трансляция которых в определенных пространственных направлениях приводит к образованию определенных модулярных структур (табл. 1, рис. 1).
Таблица 1
Возможные характеристики модулярных структур из изогональных пространственных ячеек
|
Изогон, его вершинная топология и симметрия |
Комбинация изогонов (как вариант разбиения пространства) |
Занятый изогоном решеточный комплекс и его симметрия |
Матрица значений || i || и m, представленных в виде ((iv ir ig) m) |
Симметрия модулярной структуры (z) |
|
Тригональная призма {344} (`43m) |
12{344} |
G (6m2) vD2z (2mm) |
((005)0); ((605)1); ((095)1) |
P6/mmm (2) I41/amd (8) |
|
Куб {444} (m3m) |
8{444} |
P (m3m) |
((006)0); ((806)1); ((012.5)1) |
Pm3m (1) |
|
Гексагональная призма {644} (6/mmm) |
6{644} |
P (6/mmm) |
((008)0); ((012.8)0); ((012.8)1) |
P6/mmm (1) |
|
Усеченный октаэдр {466} (m3m) |
4{466} |
I (m3m) |
((008)0) |
Im3m (2) |
Установлено, что для каждого варианта разбиения пространства симметрия G33(z) образующихся по законам транскрипции и эволюции полиэдрических модулярных структур R33(Tim, Ek) и характеристики занятых полиэдрами решеточных комплексов находятся во взаимно однозначном соответствии (см. табл. 1).
При значениях параметра m больше 1 возможно образование локальных структур с пустыми пространственными ячейками, которые на стадии трансляции приводят к образованию модулированных модулярных структур. Это происходит и при заполнении изогональных ячеек определенной геометрии и топологии из числа возможных в комбинации изогонов (табл. 2, рис. 1).
Упаковка модулей в концентрационно модулированных модулярных структурах соответствует кодам их упаковки, представляемой матрицей ||СР|| структурного кода. В данном случае для множества модулярных R33 -структур может быть установлен изоморфизм информационных данных, закодированных в (||i||,m,||k||) и (||CP||). Однако многообразие вариантов модулированных модулярных R33-структур определяется множеством вариантов структурированного ячеистого 3D пространства, которое используется в эволюционной модели для получения модулярных структур (см. табл.2). Геометрия и топология модуля, а также ограничения, накладываемые на плотность упаковки этих модулей в матрицах ||СР|| кодов модулярных структур, существенно снижают их возможное число.
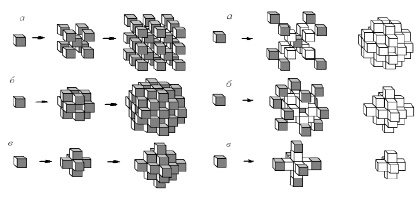
Рис. 1. Слева – динамика роста гексаэдрических R3{444},imk –структур, характеризующихся матрицей значений || i || и m, представленной в виде ((iv ir ig) m), и эволюционирующих с помощью вершин – ((8.0.0)0) (а), с помощью ребер – ((0.12.0.)0) (б) и с помощью граней ((0.0.6)0) (в). Справа – рост гексаэдрических R3{444},imk –структур, характеризующихся матрицей значений || i || и m, представленной в виде ((iv ir ig) m), и эволюционирующих с помощью вершин – ((8.0.0)1) (а), с помощью ребер – ((0.12.0.)1) (б) и с помощью граней ((0.0.6)1). Справа показаны конфигурации пустот – «пор» – для соответствующих микропористых структур
Таблица 2
Возможные характеристики модулированных модулярных структур из занятых изогональных пространственных ячеек в соответствующей комбинации изогонов
|
Топология занятого изогона |
Занятый решеточный комплекс и его симметрия |
Комбинация изогонов |
Матрица || i ||, m в виде ((iv ir ig) m) |
Симметрия модулярной структуры (z) |
|
{333} |
F2 (43m) E2z (3m) |
8{333}+6{3333} |
((006)0) ((031)0) |
Fm3m (8) P63/mmc (4) |
|
{3333} |
F (m3m) Pc (6m2) |
6{3333}+8{333} |
((0120)0) ((062)0) |
Fm3m (4) P63/mmc (2) |
|
{344} |
G (6m2) 2G2z (3) |
4{344}+4{644} 8{344}+2{644} |
((032)0) ((065)1) |
P6/mmm (2) P6/m (8) |
|
{444} |
C (4/m) |
4{444}+6{344} |
((802)0) ((042)0) |
Pm3m (2) |
|
{644} |
P (6/mmm) |
4{644}+4{344} |
((062)0) |
P6/mmm (1) |
|
{366} |
D (43m) |
6{366}+2{333} |
((004)0) |
Fd3m (8) |
|
{844} |
P (4/mmm) |
4{844}+2{444} |
((006)0) |
P4/mmm (1) |
|
{12.44} |
P (6/mmm) |
4{12.44}+2{344} |
((008)0) |
P6/mmm (1) |
|
{3434} |
P (m3m) |
4{3434}+2{3333} |
((080)0) |
Pm3m (1) |
|
{3444} |
F (m3m) P (m3m) |
3{3444}+{444}+{333} 2{3444}+{3434}+2{444} |
((606)0) ((006)0) |
Fm3m (4) Pm3m (1) |
|
{466} |
F (m3m) |
2{466}+{3434}+2{366} |
((080)0) |
Fm3m (4) |
|
{468} |
P (m3m) F (m3m) I (m3m) |
2{468}+{466}+{444} 2{468}+{388}+{366} 2{468}+2{844} |
((006)0) ((006)0) ((080)0) |
Pm3m (1) Fm3m (4) Im3m (2) |
Генетическая принадлежность и модулярная сложность структур
Генетические структурные коды вида {M(G30)(||i||,m,||k||)}[S(LC)i (G33(z))] содержат информацию, которая существенно расширяет понимание генетической принадлежности и модулярной сложности структур. Это информация о локальной структуре в виде алгоритма ее формирования (||i||,m,||k||) и информация об особенностях геометрии и топологии модуля-зародыша M, генетически предопределяющая модулярную сложность структур. Проиллюстрируем данное утверждение на примере некоторых модульных структур.
В соответствии с основными положениями структурной кристаллографии и кристаллохимии представление модульной R33–структуры кристалла может быть осуществлено с помощью описания состава и конфигурации d–мерного модуля Мd, 3–d и закона его упаковки в 3D пространстве в (3–d) кристаллографически независимых направлениях. Тогда код этих структур может быть представлен следующим образом:
R33{M d, 3–d (G3d) (CP) 33–d}[(LC)33 (G33 (z))].
Кристаллохимическую часть описания R33–структуры (описание в фигурных скобках) можно выразить через описания подструктур меньшей размерности и представить следующим образом:
R33{R22 {R11 {R00}}}.
В данном представлении
R22{Md, 2–d (G2d) (CP)22–d}, где (d = 0, 1), R22{M2, 0} при d = 2;
R11{Md, 1–d (G1d) (CP)11–d}, где (d = 0), R11{M1, 0} при d = 1;
R00{M0, 0} при d = 0.
Рассмотрим одно из возможных представлений R22–подструктур R33–структуры через 0–мерные модули М0.2: R22{M0,2 (G20) (CP)22}. Код упаковки модулей (CP)22, в которой содержится основная структурная информация, может быть представлен разными способами [4].
Способ 1. Представление (CP) в виде описания закона чередования модулей M0,2 вдоль независимых кристаллографических направлений в 2D пространстве.
Способ 2. Представление (CP) в виде описания характеристик решеточного комплекса (LC)22, в соответствии с которым упакованы модули M0,2 в R22–структуре.
Способ 3. Представление (CP) в виде закона заполнения определенных ячеек 2D пространства структурно совместимыми с этими ячейками модулями M0,2.
Для описания упаковочного кода (СР)22 модулей М0,2 в слоях удобно использовать третий способ. В этом случае вид его описания зависит от способа разбиения пространства.
Если в качестве модулей М0,2 выступают изогоны {I} (в частности, полигоны (Pg) в случае атомных слоев или полиэдры (Ph) в случае двухслойных упаковок), то упаковочный код может быть представлен комбинацией изогонов {CI} с указанием характеристик типа заполняемого изогона {I}, т.е. кристаллохимической топологии T его окружения аналогичными изогонами и позиционной симметрии S:
R22{{CI} {I}((T)-S) },
где группа симметрии S = G30.
В данном случае комбинацию изогонов {CI}, которые полностью заполняют 2D пространство, можно рассматривать как вариант его изогонального разбиения на ячейки типа {I}. Тогда для того, чтобы охарактеризовать процесс формирования R22–структуры, от ее пространственного и симметрийного описания с помощью характеристик T и S необходимо перейти к представлению, основанному на описании соответствующих эволюционных законов: ((T)-S) ® (||i||, m), где (||i||, m) может рассматриваться как матрица значений ((iv, ir, ig), m) для {Ph} и как матрица значений ((iv, ir), m) для {Pg}.
Окончательно для символьного представления R22–структуры в виде ее генетического кода имеем
R22{M 0,2 (G22) [CI] {I}((||i||, m)) }.
Необходимо отметить, что эволюционная модель формирования модулярных 3D структур и символьные образы их, представленные в виде генетических кодов, обладают следующими свойствами:
1) соответствие определенному многообразию «беспористых» модулярных структур, структурные коды которых изоморфны соответствующим генетическим кодам и обладают идентичными генетическими связями,
2) соответствие некоторому многообразию модулярных структур и возможность идентификации соответствующих структурных кодов и генетических связей между ними,
3) возможность получения множества вариантов структурирования пространства и такого же множества многообразий инверсионно модулированных модулярных структур с соответствующими им сетками генетических взаимосвязей,
4) возможность определения принципиально новых эволюционных взаимосвязей между структурами, существенно дополняющих информацию, записанную в их структурных кодах,
5) применимость для кодирования Rmn–структур с размерностью m < 3.
Указанные свойства информационных кодов могут быть использованы для компактной символьной записи модульных структур, их идентификации, систематизации и классификации, выявления новых генетических связей другими модульными структурами, вывода новых инверсионно модулированных модулярных Rmn–структур. Можно также предположить, что проанализированные выше модулированные структуры являются идеализированным вариантом представления определенных структурных состояний, возникающих в результате реализации фазово-разупорядоченного состояния на поверхности и в объеме композиционных материалов и покрытий [3, 23, 24]. Результаты анализа некоторых из этих состояний были, в частности, использованы при расчете величины эффекта синергизма при трении и износе для некоторых композиционных покрытий [21, 25 – 31].
Выводы
Предложена эволюционная модель формирования инверсионно модулированных модулярных структур кристаллов из 0D структурных модулей и соответствующая ей система генетических структурных кодов. Модулированные структуры могут быть сформированы на модулярных структурах из определенного центрального 0D модуля. Генетический структурный код включает описание геометрии и топологии модуля как генератора структуры, а также описания стадий формирования модулированной структуры с центром инверсии. Процесс формирования модулированных модулярных структур соответствует определенному эволюционному закону развития в предварительно структурированном ячеистом пространстве. Система генетических структурных кодов предназначена для выявления особенностей формирования многообразия модулированных структур, полученных на определенной модулярной структуре, для идентификации структурных модулей – генераторов вероятных модулированных модулярных структур, для выявления взаимосвязей геометрических и топологических свойств генератора и аналогичных свойств соответствующих ему инверсионно модулированных структур.

