Все методы определения значений функций принадлежности условно можно разделить на следующие группы: прямые методы, косвенные методы, L-R & dash; функции.
К первой группе методов можно отнести частотный анализ по результатам опросов экспертов.
Пример. По результатам опросов респондентов по прогнозам цены литра молока в 2016 г. получены следующие результаты (табл.1).
Ко второй группе методов можно отнести экспертные методы (например, анкетный метод нормирования, а также метод попарных сравнений).
Метод нормирования, заключается в следующем. Эксперту предлагается оценить степень принадлежности к множеству А каждого элемента из Ux1 & dash; х , соотнеся свое мнение со значениями по некоторой, заранее выбранной шкале (например, от 0 до 100%, или относительных величинах от 0 до 1, или любой другой).
Результаты опроса нескольких экспертов сводятся в матрицу опроса (табл. 2).
Затем производятся следующая последовательность действий:
- рассчитывается сумма весов, даваемых i-м экспертом всем элементам:
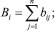
- рассчитывается относительный вес j-го элемента на основании оценки i-го эксперта:
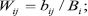
- рассчитывается результирующий вес j-го элемента:
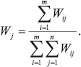
Таблица 1
Данные по опросу экспертов о прогнозируемой цене на молоко в 2016 г
|
Прогнозируемая цена молока на 2016 г., руб. |
Количество респондентов, выбравших данное значение цены |
Доля респондентов, выбравших данное значение цены |
|
46 |
68 |
0,38 |
|
48 |
52 |
0,29 |
|
50 |
43 |
0,24 |
|
52 |
17 |
0,09 |
|
Итого |
180 |
1,00 |
Таблица2
Матрица опроса нескольких экспертов
|
Эксперт |
Элементы |
Сумма |
|||||
|
1 |
2 |
… |
j |
… |
n | ||
|
1 2 … i … m |
b11 b21 … bi1 … bm1 |
b12 b22 … bi2 … bm2 |
… … … … … … |
b1j b2j … bij … bmj |
… … … … … … |
b1 b2 … bi … bm |
B1 B2 … Bi … Bm |
Пример. В табл. 3 приведены результаты опроса четырех экспертов о степени принадлежности трех элементов & dash; автомобилей «Chevrolet iva», «JeepGra dCherokee», «CheryTiggo F» множеству «Внедорожники», оцененные по 100 бальной шкале.
Таблица 3
Матрица опроса
|
Эксперт |
Элементы |
||
|
«JeepGra dCherokee» |
«Chevrolet iva» |
«CheryTiggo F» |
|
|
1 |
60 |
20 |
20 |
|
2 |
40 |
20 |
30 |
|
3 |
70 |
40 |
50 |
|
4 |
40 |
80 |
50 |
- рассчитывается сумма весов, даваемых i-м экспертом всем элементам:
Таблица 4
Матрица опроса с элементами расчетов
|
Эксперт |
Элементы |
Bi |
||
|
«JeepGra dCherokee» |
«Chevrolet iva» |
«CheryTiggo F» |
||
|
1 |
60 |
20 |
20 |
100 |
|
2 |
40 |
20 |
30 |
90 |
|
3 |
70 |
40 |
50 |
160 |
|
4 |
40 |
80 |
50 |
170 |
- рассчитывается относительный вес j-го элемента на основании оценки i-го эксперта:
Таблица 5
Матрица опроса с элементами расчетов
|
Эксперт |
Элементы |
Bi |
||
|
«JeepGrandCherokee» |
«ChevroletNiva» |
«CheryTiggo F» |
||
|
1 |
0,6 |
0,2 |
0,2 |
100 |
|
2 |
0,44 |
0,22 |
0,33 |
90 |
|
3 |
0,44 |
0,25 |
0,31 |
160 |
|
4 |
0,24 |
0,47 |
0,29 |
170 |
- рассчитывается результирующий вес j-го элемента:
Таблица 6
Матрица опроса с элементами расчетов и результатами
|
Эксперт |
Элементы |
Bi |
||
|
«JeepGrandCherokee» |
«ChevroletNiva» |
«CheryTiggo F» |
||
|
1 |
0,6 |
0,2 |
0,2 |
100 |
|
2 |
0,44 |
0,22 |
0,33 |
90 |
|
3 |
0,44 |
0,25 |
0,31 |
160 |
|
4 |
0,24 |
0,47 |
0,29 |
170 |
|
Wj |
0,43 |
0,29 |
0,28 |
|
Итак, согласно собранным данным и методу расчета множестово«Внедорожники» ={0,43/ «JeepGra dCherokee»; 0,29/ «Chevrolet iva»; 0,28/ «CheryTiggo F»}
Метод попарных сравнений, заключается в том, что только один эксперт на основе своего субъективного мнения оценивает принадлежность элемента данному множеству относительно другого элемента. Для проведения субъективных парных сравнений Т. Саати была разработана шкала относительной важности, ее модификация приведена в табл. 7:
Таблица 7
Матрица опроса с элементами расчетов и результатами
|
Шкала |
Значение |
|
1 |
Равная важность/предпочтительность |
|
3 |
Умеренное превосходство одного над другим |
|
5 |
Существенное превосходство одного над другим |
|
7 |
Значительное превосходство одного над другим |
|
9 |
Очень сильное превосходство одного над другим |
|
2, 4, 6, 8 |
Промежуточные значения шкалы |
Результаты попарного сравнения элементов заносятся в матрицу сравнения размерности n×n, где n число сравниваемых элементов. Элемент указанной матрицы выражает результат сравнения элементов i и j. Если при сравнении элементов i и j получено a(i,j)=b, то результатом сравнения элементов jи iдолжно быть a(j,i)=1/b. Очевидно, что диагональные элементы матрицы равны 1.
Т. Саати предложил упрощенную процедуру вычисления вектора w. Пусть v& dash; вектор геометрических средних строк некоторой матрицы сравнения:
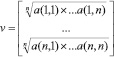
Тогда вектор wбудет определяться следующим образом:

Пример. По результатам оценки эксперта степени принадлежности трех элементов & dash; значений температур в градусах Цельсия определить множество «Холодно».
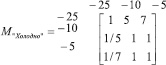
Соответствующие матрицам сравнения векторы локальных приоритетов находятся следующим образом:



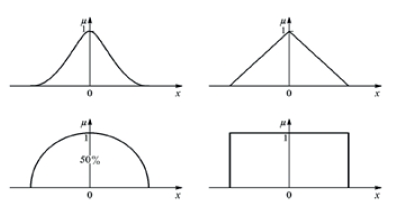
Рис. 1. Примеры L-R -функций
Итак, по данным расчетов «Холодно»={0,747/ -25; 0,134/ -10; 0,119/-5}.
Третью группу составляют способы на основе использования так называемые L-R & dash; функций (типовых форм кривых рис. 1) для задания функций принадлежности с уточнением их параметров путем приближения к реальным данным.
Пример. Если мы оцениваем параметр качественно, например, говоря: «Это значение параметра является средним», необходимо ввести уточняющее высказывание типа « Среднее значение — это примерно от a до b», которое есть предмет экспертной оценки (нечеткой классификации), и тогда можно использовать для моделирования трапециевидную функцию.
Если мы хотим выразить «приблизительно равно α», то можно использовать треугольные функции.

