Работа с рядами данных – один из основных навыков специалистов, занимающихся аналитической деятельностью.
Рассмотрим этапы построения вариационных рядов с использованием указанных функций на следующем примере.Дана оценка расходов на ЖКХ 62 респондентов (табл. 1).
Заметим, что рассматриваемая далее последовательность шагов применима и для построения атрибутивного ряда, при условии предварительного кодирования данных (присваивания числовых аналогов нечисловым значениям признака).
Шаг 1. Подготовка данных – сортировка (данный шаг можно пропустить, т.к. он служит лишь для удобства восприятия ряда). Произведем сортировку по возрастанию представленных данных по столбцу «Оцените ваши расходы на ЖКХ за последний год».
Для этого выделите весь диапазон данных, выберите в пункте меню Сервис опцию Сортировка, а затем в открывшемся окне установите столбец, по которому будет производиться сортировка и вид сортировки – по возрастанию.
После сортировки данные будут выглядеть как на рис. 2,при этом в конце ряда останутся респонденты, не ответившие на вопрос (ответы отмечены знаком «-»).
Шаг 2. Построение массива признаков. Данный шаг можно осуществить двумя способами.
1 способ: ручной ввод. Выписать по одному все встречающиеся значения исследуемого признака (например, в столбец D). Этот способ прост в том случае, если данные были отсортированы (шаг 1), но и это при большом объеме данных не позволяет избежать ошибок, а также затрачивает достаточно много времени.
2 способ: автоматический. Выбираем в меню Данные и в нем Фильтр – Расширенный фильтр. В открывшемся окне (см. рис. 3) устанавливаем переключатель на положение Скопировать результат в другое место,указываем интересующий нас интервал сходных данных в поле Исходный диапазон; указываем ячейку – место начала размещения массива признаков в окне Переместить результат в диапазон, устанавливаем флажок Только уникальные записи. Этот способ более предпочтителен.
Шаг 3. Расчет частот. Теперь выделите весь диапазон ячеек напротив выделенных признаков (например, Е2:Е19), поставьте знак «=», укажите имя функции ЧАСТОТА, после открывающихся скобок выделите массив_данных (D2:D63), а затем через точку запятой массив_интервалов – значения исследуемого признака (D2:D19). После закрытия скобок нажмите удерживая Ctrl+Shift кнопку Enter (такая комбинация клавиш для ввода функций используется всегда при работе с массивами данных).
Как видно на рис. 4, сумма всех частот равна 52, а всего было опрошено 62 респондента. Разница между количеством опрошенных и ответивших составляет как раз 10 человек.


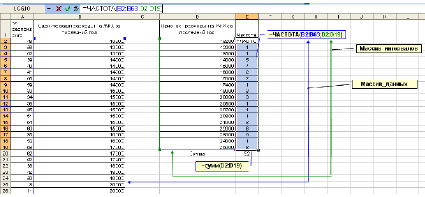
Рис. 4. Использование функции ЧАСТОТА
Этапы построения интервального вариационного ряда
Так как дискретный вариационный ряд из нашего примера содержит довольно большое число значений признака (18 значений признаков), было бы более правильно представить исходные данные в виде интервального ряда. Рассмотрим шаги построения последнего.
Таблица 1
Данные опроса по оценке расходов на ЖКХ
|
№ респондента |
Оцените ваши расходы на ЖКХ за последний год |
№ респондента |
Оцените ваши расходы на ЖКХ за последний год |
|
1 |
25000 |
32 |
25000 |
|
2 |
23000 |
33 |
15000 |
|
3 |
22000 |
34 |
15000 |
|
4 |
22000 |
35 |
16000 |
|
5 |
21000 |
36 |
15000 |
|
6 |
23000 |
37 |
- |
|
7 |
22000 |
38 |
18000 |
|
8 |
20000 |
39 |
14000 |
|
9 |
25000 |
40 |
14000 |
|
10 |
- |
41 |
14000 |
|
11 |
20000 |
42 |
18000 |
|
12 |
23000 |
43 |
- |
|
13 |
23000 |
44 |
20000 |
|
14 |
23000 |
45 |
15000 |
|
15 |
21000 |
46 |
- |
|
16 |
21000 |
47 |
17400 |
|
17 |
- |
48 |
13200 |
|
18 |
- |
49 |
- |
|
19 |
25000 |
50 |
18000 |
|
20 |
25000 |
51 |
15000 |
|
21 |
25000 |
52 |
16000 |
|
22 |
25000 |
53 |
- |
|
23 |
25000 |
54 |
15000 |
|
24 |
24000 |
55 |
14000 |
|
25 |
22000 |
56 |
13300 |
|
26 |
22000 |
57 |
13500 |
|
27 |
20500 |
58 |
17000 |
|
28 |
20800 |
59 |
14000 |
|
29 |
- |
60 |
15000 |
|
30 |
22000 |
61 |
- |
|
31 |
20700 |
62 |
17000 |
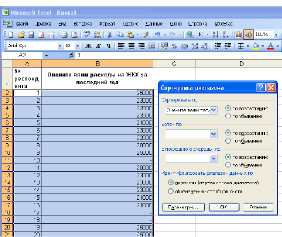
Рис. 2. Сортировка данных
Рис. 3. Расширенный фильтр
Шаг 1. Определение количества интервалов. Воспользовавшись формулой Стержеса, вычислим рекомендуемое количество интервалов: r≈1+3,2*lg(n)≈1+3,2*lg(62)≈6,7. Округлив полученное значение до целых, определяем, что ряд будет содержать 7 интервалов (ячейка Е1 на рис. 5).
Шаг 2. Определение шага (длины интервала). Для того чтобы интервалы ряда были равными, вычислим шаг следующим образом: определим разность между максимальным и минимальным значениями в исходном ряду данных, а затем разделим ее на количество интервалов (ячейка E2 на рис. 5).
Рис. 5. Построение интервального ряда
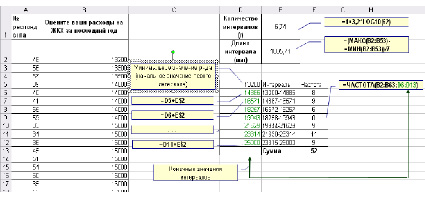
Шаг 3. Восстановление массива интервалов. Теперь, начиная от минимального значения исходных данных, с учетом вычисленной длины интервалов, создадим массив интервалов (диапазон ячеек D5:D12 на рис. 5).
Шаг 4. Расчет частот. Расчет частот производится с помощью функции ЧАСТОТА так же, как и в случае дискретного ряда (см. шаг 3 в этапах построения дискретного ряда), при этом в качестве массива интервалов используются конечные значения рассчитанных интервалов (диапазон ячеек D6:D12 на рис. 5).
Рассмотренная последовательность шагов проста, но не самая оптимальная в плане времени обработки данных (более удобен инструмент «сводные таблицы»). Однако дидактический эффект заключается в раскрытии этапов построения одномерных рядов данных, понимания их сущности и видов, а также различие способов их построения.

