Для реализации процедуры Регрессия необходимо: выбрать в меню Сервис команду Анализ данных. В появившемся диалоговом окне Анализ данных в списке Инструменты анализа выбрать строку Регрессия.
Рис.1. Окно «Регрессия»
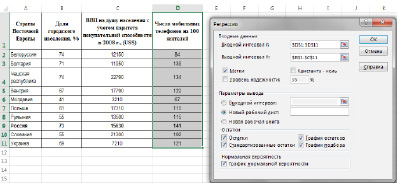
В появившемся диалоговом окне (рис.1) задать:
Входной интервал Y– диапазон (столбец), содержащий данные со значениями объясняемой переменной;
Входной интервал Х– диапазон (столбцы), содержащий данные с заголовками.
Метки – флажок, который указывает, содержат ли первые элементы отмеченных диапазонов названия переменных (столбцов) или нет;
Константа-ноль– флажок, указывающий на наличие или отсутствие свободного члена в уравнении (а);
Уровень надежности– уровень значимости, (например, 0,05);
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона, в котором будет сохранен отчет по построению модели;
Новый рабочий лист– поставить значок и задать имя нового листа (Отчет – регрессия), в котором будет сохранен отчет.
Если необходимо получить значения и график остатков, а также график подбора (чтобы визуально проверить отличие экспериментальных точек от предсказанных по регрессионной модели), установите соответствующие флажки в диалоговом окне.
Рассмотрим результаты регрессионного анализа (рис. 2, 3).
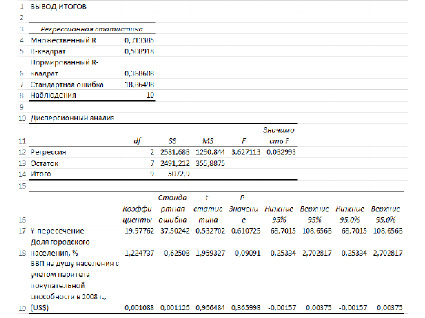
Рис. 2. Вывод итогов регрессионного анализа
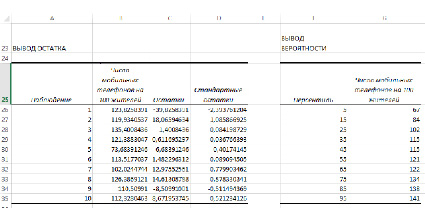
Рис. 3. Вывод остатков и вероятности по результатам регрессионного анализа
Множественный R – коэффициент корреляции
R-квадрат – это коэффициент линейной детерминации. Коэффициент является одной из наиболее эффективных оценок адекватности регрессионной R2модели, мерой качества уравнения регрессии в целом (или, как говорят, мерой качества подгонки регрессионной модели к наблюденным значениям.
Если R-квадрат > 0,95, говорят о высокой точности аппроксимации (модель хорошо описывает явление). Если R-квадрат лежит в диапазоне от 0,8 до 0,95, говорят об удовлетворительной аппроксимации (модель в целом адекватна описываемому явлению). Если R-квадрат < 0,6, принято считать, что точность аппроксимации недостаточна и модель требует улучшения (введения новых независимых переменных, учета нелинейностей и т. д.).
Нормированный R-квадрат – скорректированный (адаптированный, поправленный) коэффициент детерминации.
Недостатком коэффициента детерминации R-квадратявляется то, что он увеличивается при добавлении новых объясняющих переменных, хотя это и не обязательно означает улучшение качества регрессионной модели. В этом смысле предпочтительнее использовать нормированный, который в отличие от R-квадрат может уменьшаться при введении в модель новых объясняющих переменных, не оказывающих существенное влияние на зависимую переменную.
Наблюдения – число наблюдений (в нашем случае 10 стран).
Df– число степеней свободы связано с числом единиц совокупности и с числом определяемых по ней констант.
F и Значимость F позволяют проверить значимость уравнения регрессии, т.е. установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.
SS – Сумма квадратов отклонений значений признака Y.
MS – Дисперсия на одну степень свободы.
F – Наблюдаемое (эмпирическое) значение статистики F, по которой проверяется гипотеза равенства нулю одновременно всех коэффициентов модели. Значимость F – теоретическая вероятность того, что при гипотезе равенства нулю одновременно всех коэффициентов модели F-статистика больше эмпирического значения F.
На уровне значимости α=0,05 гипотеза H0:b1=0отвергается, если Значимость F<0.05, и принимается, если Значимость F
Значения коэффициентов регрессии находятся в столбце Коэффициенты и соответствуют:
У-пересечение – a;
переменная XI – b1;
переменная Х2 – b2 и т. Д.
Таким образом, получена следующая модель регрессии:
Y=1.2247X1+0.00108X2+19.9776
t-статистика соответствующего коэффициента.
P-Значение – вероятность, позволяющая определить значимость коэффициента регрессии. В случаях, когда Р-Значение>0,05, коэффициент может считаться нулевым, что означает, что соответствующая независимая переменная практически не влияет на зависимую переменную.
В нашем случае оба коэффициента оказались «нулевыми», а значит обе независимые переменные не влияют на модель.
Нижние 95% – Верхние 95% – доверительный интервал для параметра , т.е. с надежностью 0.95 этот коэффициент лежит в данном интервале. Поскольку коэффициент регрессии в исследованиях имеют четкую интерпретацию, то границы доверительного интервала для коэффициента регрессии не должны содержать противоречивых результатов. Так, например, «Доля городского населения, в %» не может лежать в интервале -0,25≥b1≥2,7. Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть.
Предсказанное Y - теоретические (расчетные) значения результативного признака.
Остатки – остатки по модели регрессии.
На основе данных об остатках модели регрессии был построен график остатков (рис. 4) и график подбора – поле корреляции фактических и теоретических (расчетных) значений результативной переменной (рис.5).
Рис. 4. График остатков по значениям признака «Доля городского населения, %»
Рис. 5. График подбора для признаков «Доля городского населения, %» и «Число мобильных телефонов на 100 жителей»
Рассмотрение графиков подбора позволяет предположить, что, возможно, качество модели можно усовершенствовать, исключив данные по Белоруссии как аномальные значения.

